三角形的数量

常看到的一个数学题，在三角形的边上有若干个点，然后问可以有几个三角形。

题目

三角形的 2 条边上分别有 m 和 n 个点（不包括三角形的顶点），这些点分别同这两条边相对的顶点有连线，这样组成了一个复杂的图形，问这个图形中包含了多少个不同的三角形。

题解

一个排列组合题目。

考虑以 A 为顶点的三角形数量， 线段 [A1,B] 上任取 2 点，同 A 可以组成三角形，因此总数量为 C(n+2, 2)。与 [A1,B] 类似的线段，共有 m+1 条。总数为：。

考虑以 B 为顶点的三角形数量， 线段 [B1,A] 上任取 2 点，同 B 可以组成三角形，因此总数量为 C(m+2, 2)。与 [B1,A] 类似的线段，共有 n+1 条。总数为：。

这两种统计方法，有重复统计，即同时以 A,B 为顶点的三角形。这种三角形的数量为  个。

因此，总数为：。

举例

这样我们假设 m=1，n=2，这样可以构成如下图所示情况：

数学计算

根据上面的计算公式：

总数为：12+9+6=15。

手工统计

以 A 为顶点，线段 [A1,B] 上任取 2 点，组成的三角形

先统计单个三角形，有 3 个。如下图所示：

再统计两个三角形构成的新三角形，有 2 个。如下图所示：

再统计三个三角形构成的新三角形，有 1 个。如下图所示：

这样合计是：3+2+1=6 个。

以 A 为顶点，线段 [C,B] 上任取 2 点，组成的三角形

先统计单个三角形，有 3 个。如下图所示：

再统计两个三角形构成的新三角形，有 2 个。如下图所示：

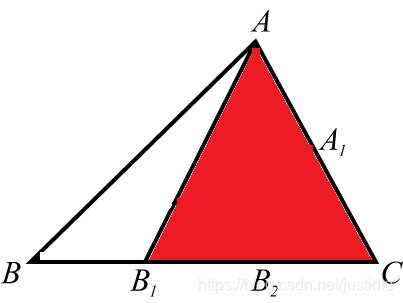
再统计三个三角形构成的新三角形，有 1 个。如下图所示：

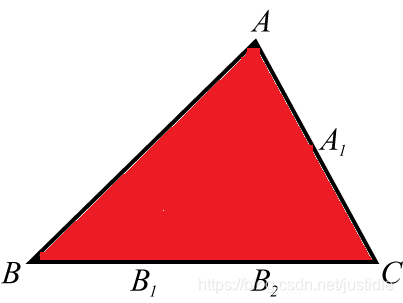
和上一个过程是一样的，合计也是 3+2+1=6 个。

这样以 A 为顶点的三角形一共有 6+6=12 个。

以 B 为顶点，线段 [B1,A] 上任取 2 点，组成的三角形

先统计单个三角形，有 2 个。如下图所示：

注意：标注为 1 的三角形被重复统计。

再统计两个三角形构成的新三角形，有 1 个。如下图所示：

注意：我们可以看出  其实已经被统计过了。

合计是 2+1=3 个。

以 B 为顶点，线段 [B2,A] 上任取 2 点，组成的三角形

注意：我们可以看出  其实已经被统计过了。

合计是 2+1=3 个。

以 B 为顶点，线段 [C,A] 上任取 2 点，组成的三角形

注意：我们可以看出  其实已经被统计过了。

合计是 2+1=3 个。

这样以 B 为顶点的三角形一共有 3+3+3=9 个。

重复统计的三角形

如上图所示，以 A 和 B 为顶点，再选择一个点，构成的三角形被重复统计。，合计 6 个。

最终的手工统计数据为：12+9-6=15 个。