数据结构（串，数组和广义表）

洋葱12358

已于 2022-04-27 16:21:11 修改

阅读量1.3k

点赞数 1

文章标签：数据结构 linq p2p

于 2022-03-06 14:03:24 首次发布

本文链接：https://blog.csdn.net/jxttutu/article/details/123309117

版权

4.1串的定义

串（字符串），是由多个字符组成的线性表，是一种内容受限的线性表

串长：串中字符的个数

空串：零个字符的串

子串：串中任意个连续的字符组成的子序列。包含字串的串相应称为主串

真子串：不包含本身的子串

空格串：由一个或多个空格组成的串

字串位置：子串中第一个字符在主串中出现的位置

串相等：两个串的长度相同并且各个位置的字符都相同

4.3串的类型定义，存储结构及其运算

4.3.1串的抽象数据类型定义：p89

4.3.2串的存储结构

串的存储结构包括顺序存储结构和链式存储结构

一.串的顺序存储结构（使用更多）

类型定义：

#define MAXSIZE 255        //设置串的最大长度
typedef struct
{
    char ch[MAXSIZE+1];    //存储串的一维数组。多数情况下，串的下标从1开始，下标为0的位置闲置
    int length;            //故设置空间为MAXSIZE+1
}SString;

一般情况下，为了便于操作，串的下标为0的位置闲置，从下标为1的位置开始存储

二.串的链式存储结构

字符占1type，二指针占4type，如果每个字符都只占一个结点，那么存储密度过小。因此采用块链结构存储链串

结构示意图：

类型定义：

#define chunksize 80;        //块的最大长度

typedef struct Chunk         //定义块
{
    char Chunk[chunksize];   //每个块所存储的字符的空间
    Chunk *next;             //指向下一个块的指针
}Chunk;

typedef struct                //定义链串
{
    Chunk *head,*tail;        //头尾指针
    int length;               //串当前的长度
}LString;

4.3.3串的模式匹配算法

子串的定位运算通常称为串的模式匹配或串匹配。一般将主串S称为正文串，将子串T称为模式串。该算法即在主串中查找子串

一.BF算法（暴力破解）

算法4.1BF算法

算法步骤：1.分别利用指针i和j指示主串S和模式串T当前正待比较的字符位置，i初值为pos，j初值为1

2.如果两个串均未到达串尾，即i和j分别小于S和T的串长时，则循环执行：

*1.S.ch[i]和T.ch[j]比较，如果相等，则都指向下一位置

*2.如果不相同，指针后退重新匹配，从主串的下一字符(i = i - j + 2)起再重新和模式串第一个字符比较

3.如果j>T.length,说明匹配成功，返回字串位置(i-T.length),否则失败，返回0

关于(i = i-j+2)的解释：i = i - j + 2是i从当前位置减去已经匹配过j次的长度j，回到最初的位置，然后再+1到下一位置重新匹配（+2————i-j+1+1，从下标1开始存储）

算法描述：

int Index_BF(SString S,SString T,int pos)(1<=pos<=S.length)
{
    int i = pos,j = 1;                //j表示模式串匹配位置，i表示文本串匹配位置
    while(i<=S.length&&j<=T.length)   //循环条件
    {
        if(S.ch[i]==T.ch[j])          //比较两串
        {
            i++,j++;                  //如果匹配成功，则两者均后移继续匹配
        }
        else                          //如果匹配失败，i和j都要回溯，i要回到开始的下一位，j从头
        {i=i-j+2，j = 1;}
    }
    if(j>T.length)                    //匹配成功，返回字串位置
    return i - T.length;
    else                              //匹配失败，返回0
    return 0;
}

算法分析：设m和n分别为子串和主串长

最好情况下，平均时间复杂度为O(m+n)

最坏情况下，平均时间复杂度为O(m*n)

算法4.2KMP算法（下标从1开始）

前缀：包含首字母，不包含尾字母的所有子串

后缀：包含尾字母，不包含首字母的所有子串

最长相等前后缀：某个字符前（不包含本身）的子串的最长的相等的前后缀长度

前缀表：模式串中每个字符其前的最长相等前后缀的长度组成的顺序表

设文本串"aabbaabbaaf',模式串"aabbaaf"

主串		a	a	b	a	a	b	a	a	f
子串		a	a	b	a	a	f
下标	0	1	2	3	4	5	6	7	8	9
前缀表		0	1	2	1	2	3

如上图匹配过程中，找出与f前的后缀相等的前缀的后一位继续匹配，其下标即是最长相等前后缀的长度加1，即f对应的前缀表

next数组：用来存储前缀表的数组

手算next数组：规定next[1] = 0,next[2] = 1;

next[j]:模式串中第j位字符的前j-1位字符组成的子串的最长相等前后缀长度+1（下标从1开始），也是匹配冲突时需要回溯的下标值

next数组的代码实现

void GetNext(SString T,int next[])
{
    int i = 1,j = 0;        //设置初始比较位置
    next[0] = 0;            //初赋值
    while(i < T.length)     //循环条件
    {
        if(j==0||T.ch[i]==T.ch[j])    //找最大相对前后缀，每有一个前缀字符和后缀字符相等，最大
        {                             //数+1，并填入当前位置的前缀表，ij同时后移比较下一个
            next[++i]=++j;    
        }
        else                
        j = next[j];                 //如果不同，相当于j回溯比较，再跟之前的比，找前后缀
    }
}

算法4.2KMP算法

算法描述：

int KMPindex(SString S,SString T,int pos)
{
    int i = pos,j = 1;                //i表示主串开始查找的位置，j表示模式串开始比较的位置
    while(i<=S.length&&j<=T.length)   //条件
    {
        if(j==0||S.ch[i]==T.ch[j])    //如果匹配成功
        {
            i++,j++;                  //后移继续匹配
        }
        else                          //匹配失败
        j = next[j];                  //模式串回溯到前缀表指示的位置（相当于模式串右移，相等前
    }                                 //缀跑到相等后缀的位置继续比较
    if(j>T,length)                    //匹配成功
    return i-T.length;
    else                              //匹配失败
    return 0;
}

4.4数组

4.4.1数组的类型定义

数组是由类型相同的数据元素构成的有序集合，每个元素称为数组元素

一维数组可以看成是一个线性表，二维数组可以看成数据元素是线性表的线性表

二维数组的逻辑结构：非线性结构：每个数据元素即在行表中，也在列表中

线性结构：该线性表的每个元素依然是线性表

三维数组：二维数组中的元素又是一维数组

n维数组：n-1维数组中的元素又是一个一维数组

数组一旦被定义，它的维数和维界就不再改变。因此除了初始化和销毁之外，数组只有存取元素和修改元素的操作。

结论：线性表是数组结构的特例，数组结构是线性表的拓展

4.4.2数组的顺序存储

由于数组一般不做插入或删除操作，因此采用顺序存储结构表示数组比较合适

由于存储单元是一维结构，而数组可能是多维结构。则用一组连续存储单元存放数组元素就有约定次序的问题(即多维关系如何映射到一维关系)

①：以行序为主序的存储方式

②：以列序为主序的存储方式

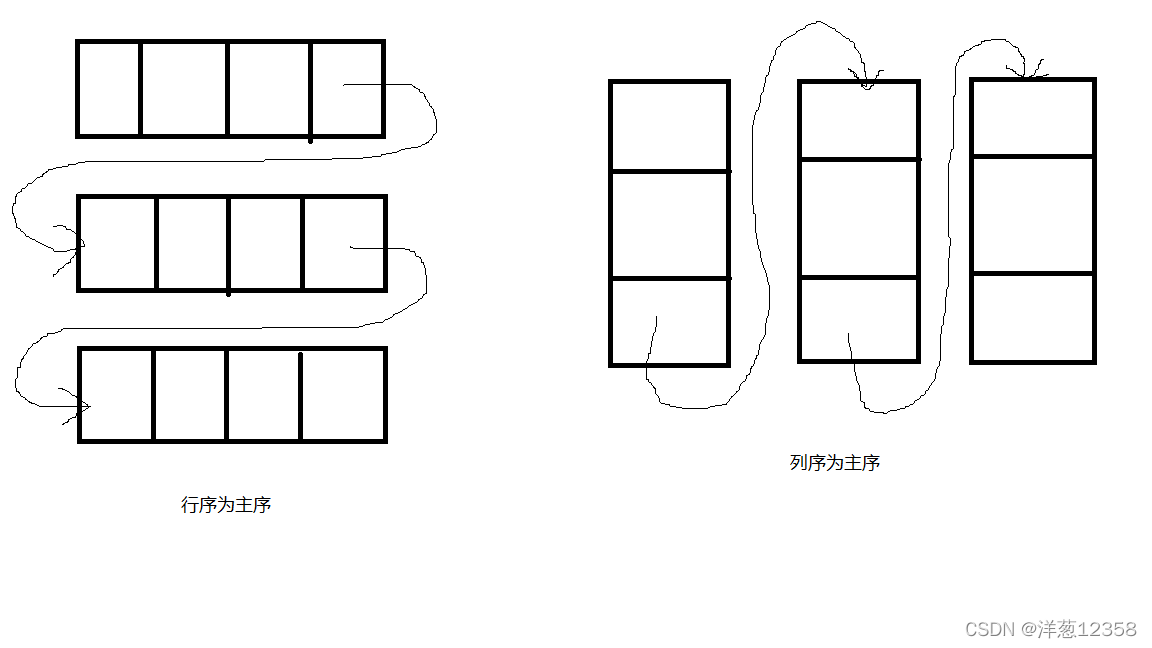
由此，对于数组，一旦规定了其维数和维界，便可为其分配空间。反之，只要给出一组下标便可求出相应数组元素的存储位置：

一维数组： $LOC(i) = LOC(0) + i * L$

（i为前面元素个数，L为每个元素所占空间）

二维数组： $LOC(i,j) = LOC(0,0) + (i*n+j)*L$

(前i行都填满了，j为本行前有多少元素)

三维数组a[m1][m2][m3]: $LOC(i,j,k) = LOC(0,0,0) + (i*m2*m3 + j*m3 + k)*L$

以此类推

4.4.3特殊矩阵的压缩存储

在数值分析中经常出现阶数很高的矩阵，同时矩阵中有很多值相同的元素或0元素。为了节约存储空间，可以对这类矩阵进行压缩存储。

压缩存储：多个值相同的元只分配一个存储空间，对零元不分配空间

假若相同的元素或零元素在矩阵中的分布有一定规律，或0元多。则称此类矩阵为特殊矩阵，主要包括：对称矩阵，三角矩阵，对角矩阵，稀疏矩阵等。

1.对称矩阵

对称矩阵中的元满足以下特性

$a_{i,j} = a_{j,i}$ 1<=i,j<=n

对于对称矩阵，可以为每一对对称元分配一个存储空间。则可将n^2个元压缩到n(n-1)/2个元的空间中，以行序为主序存储其下三角(包括对角线)中的元。

假设以一维数组sa[n * (n - 1) / 2]作为n阶对称矩阵A的存储结构，则sa[k]和矩阵元a_{i,j}存在一一对应的关系如下：

$k = \begin{cases} i(i - 1)/2+j-1 & \text{ if } i\geqslant j \\ j(j-1)/2+i-1 & \text{ if } i<j \end{cases}$

ps:前有i行，共i(i-1)/2个元素，加上本行前j-1个元素

k = 0,1,2....n(n+1)/2-1

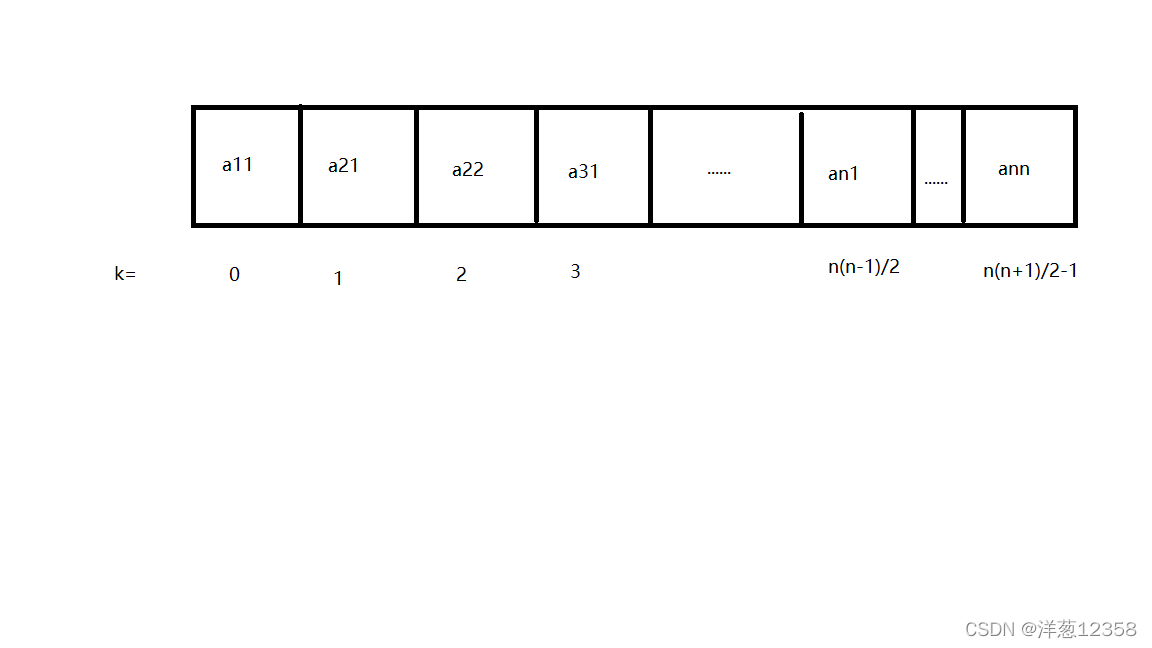
2.三角矩阵

以主对角线划分，三角矩阵有上三角矩阵和下三角矩阵。上三角矩阵是指矩阵下三角（不包括对角线）中的元均为常数c或0的n阶矩阵。下三角矩阵与之相反。

对三角矩阵进行压缩存储，除了和对称矩阵一样，再加一个存储常数c的存储空间即可

（1）上三角矩阵

sa[k]和矩阵元aij之间的关系为

$\begin{cases} (i-1)(2n-i+2)/2+(j-i) & \text{ if } i\leqslant j \\ n(n+1)/2& \text{ if } i > j \end{cases}$

（2）下三角矩阵

sa[k]和矩阵元aij之间的关系为

$\begin{cases} i(i-1)/2+j-1 & \text{ if } i\geqslant j \\ n(n+1)/2 & \text{ if } i<j \end{cases}$

3.对角矩阵

对角矩阵的所有非零元都集中在以对角线为中心的带状区域中。也可按某个规则(或以行为主，或以对角线为主的顺序)压缩到一个一维数组上

例：以对角线存储（二维数组）

$\begin{pmatrix} 8&2 &3 &0 &0 &0 \\ 2& 4& 0 & 3& 0 &0 \\ 5&7 &7 &6 &8 &0 \\ 0& 9 &6 &9 &1 &5 \\ 0& 0 &6 &1 &4 &2 \\ 0& 0 &0 &2 &8 &3 \end{pmatrix}$

结果为 $\begin{pmatrix} & & 3& 3& 8&5 \\ & 2& 0& 6& 1& 5\\ 8& 2& 7& 9& 4 &3 \\ 4& 7 & 6 & 1 & 8 & \\ 5& 9 & 6 & 2 & & \end{pmatrix}$

4.稀疏矩阵

稀疏矩阵：在m*n的矩阵中有t个非零元，设

$\delta = t/(m*n)$

若 $\delta\leqslant 0.05$ 则称该矩阵为稀疏矩阵

稀疏矩阵的存储方法有：三元组法，十字链表法

(1)三元组法

三元组（i，j，aij）和矩阵维数m*n——唯一确定矩阵中的一个非零元

压缩存储原则：存各非零元的值，行列位置和矩阵行列数。

三元组的不同表示方法可以决定稀疏矩阵不同的压缩存储方法。

注：为更可靠的描述信息，通常再加一个总体信息：总行数，总列数，总非零元个数（通常存放在0下标位置）

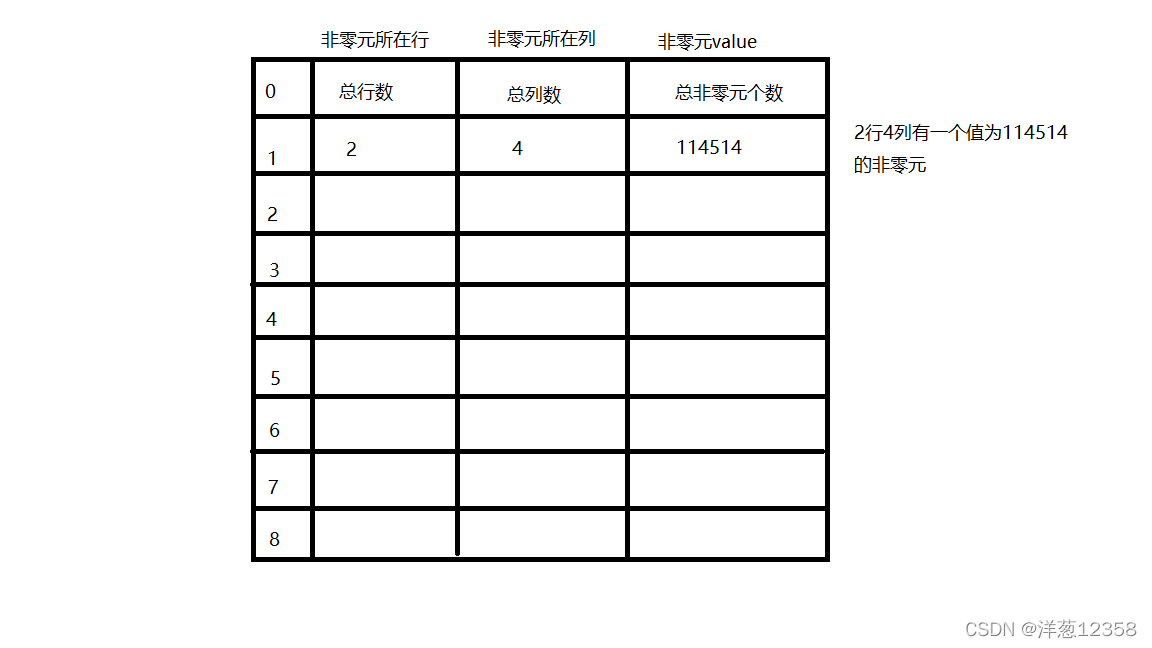
优点：非零元在表中按行序有序存储，便于进行依行序顺序处理的运算

缺点：不能随机存取，若按行号查找某一行中的非零元，需从头查找

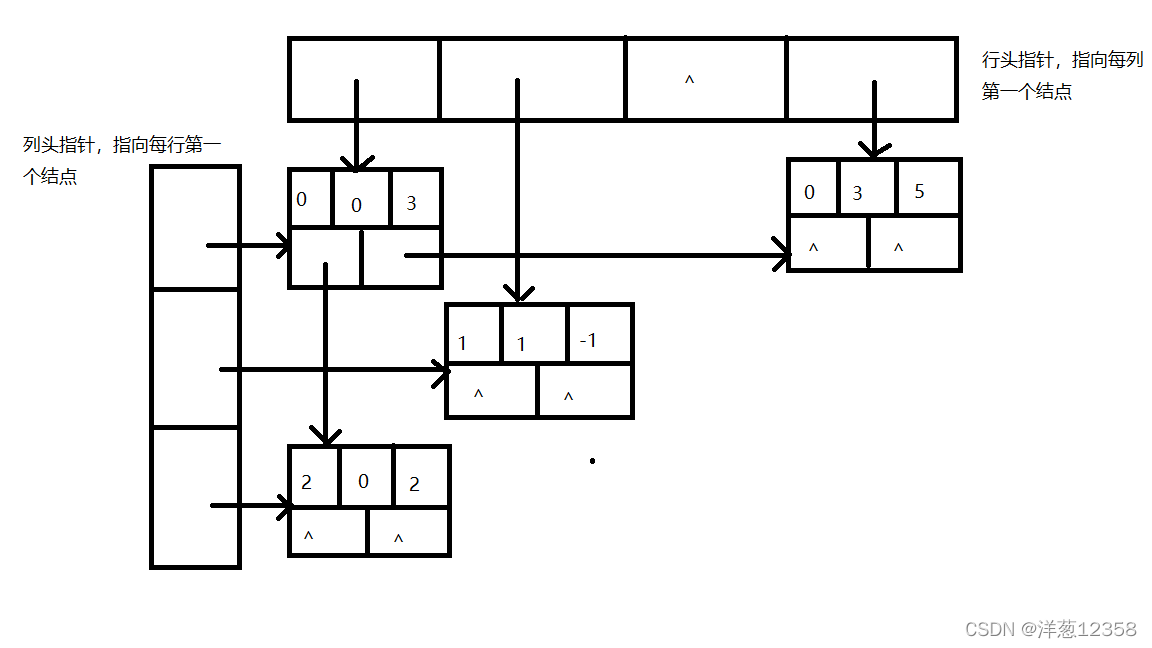
(2)十字链表法

优点：灵活地插入因运算产生的新非零元素，删除因运算产生的新0元，实现各种运算

结点结构：

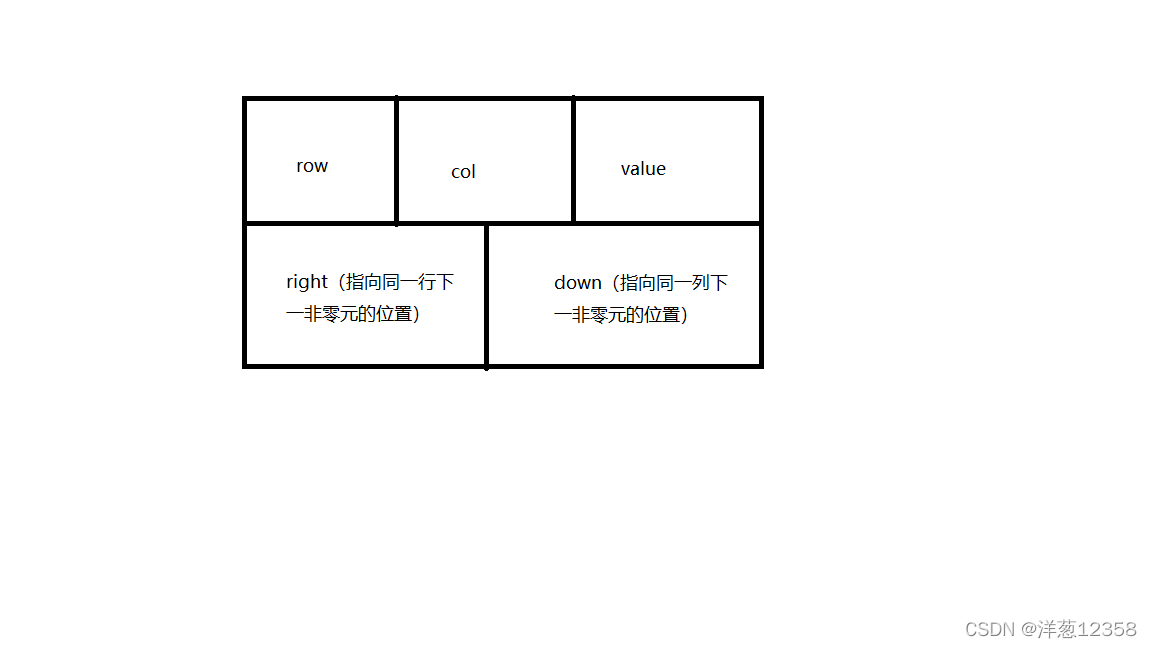
例：对于矩阵

$\begin{pmatrix} 3 &0 &0 &5 \\ 0 & -1 &0 & 0\\ 2& 0 & 0 & 0 \end{pmatrix}$ 其十字链表结构为：

4.5广义表

4.5.1广义表的定义

LS = (a1,a2....an)

LS是广义表表名，n是表长，ai称为元素。元素既可以是单个元素（原子），也可以是广义表（子表）。习惯上大写字母表示广义表，小写字母表示原子。

表头：广义表的第一个元素，可以是单原子，也可以是子表

表尾：取出除了表头以外的元素构成的表。表尾一定是广义表

例： A = ()——长度为0，深度为1

B = (e)——只有一个原子e，长度为1，深度为1，表头为e，表尾为()

C = (a,(b,c,d))——长度为2，深度为2,表头为a，表尾为((b,c,d))

D = (A,B,C)——D = ((),(e),(a,(b,c,d)))——长度为3，深度为3，表头为()

表尾为((e),(a,(b,c,d)))

E = (a,E)——E = (a,(a,(a,....)))——长度为2，深度无穷，表头为a，表尾为(E)

F = (())——长度为1，深度为2，表头表尾均为()

广义表的性质：

（1）广义表中元素有相对次序，一个直接前趋，一个直接后继

（2）广义表长度定义为最外层括号包含的元素个数

（3）广义表深度定义为该广义表展开后所含括号的重数

注：原子深度为0，空表深度为1

（4）广义表的元素可以是子表，子表的元素还可以是子表......。所以广义表是一个多层次的结构

（5）广义表可为其他广义表共享：即广义表的元素是另一个广义表

（6）广义表可以是一个递归的表，即广义表可以是本身的一个子表

洋葱12358

关注

1
点赞
踩
5

收藏

觉得还不错? 一键收藏
0
评论
数据结构（串，数组和广义表）

4.1串的定义串（字符串），是由多个字符组成的线性表，是一种内容受限的线性表串长：串中字符的个数空串：零个字符的串子串：串中任意个连续的字符组成的子序列。包含字串的串相应称为主串真子串：不包含本身的子串空格串：由一个或多个空格组成的串字串位置：子串中第一个字符在主串中出现的位置串相等：两个串的长度相同并且各个位置的字符都相同4.3串的类型定义，存...
复制链接

扫一扫