路径导航与启发式搜索

路径导航与启发式搜索

问题介绍

介绍需要求解的问题

随着生活水平的不断发展，我们出行的需求越来越高，需要到达的目的地也越来越远，很多地方都是我们不熟悉的地方。在那些地方怎么才能从一个点到达另一个点？在这么多可能的路径中哪一条才是最短的？或者说，车流量最少的、速度最快的、花费时间最少的、途径收费项目最少的……

这样的问题，在现实生活中，我们成为路径导航问题，或者是寻路问题等。

模型的建立

现在把问题抽象成一个长、宽都是100的正方形，在这个正方形中依次排布了100×100的单位边长为1的小正方形，小正方形表示的是每个点。用2种不同的颜色表示每个点的含义：例如，黑色表示这是一个障碍物，不能通行；白色表示这个点是可以通行的道路。

不失一般性，上面的模型也适用于现实中的导航。100×100的正方形，可以类似地扩展成200×200、1000×800。同时，道路就用白色的点表示，建筑物是黑色的点，河流是黑色的点，但是河流上的桥梁是白色的点……

在这样一张地图上，给定一个起点，给定一个终点，需要找到一条从起点到终点的合法路径，并尽可能使得这条路是最短的。我们定义最短，意思是经过的步数最少，此时每经过一个小正方形，权重加1。

不失一般性，这样找到的路径在现实中也是有意义的。例如，在上面的求解中，每经过一个小正方形，权重加1，如果在现实生活中，我们想要找到一条花费时间最少的路（尽管这条路不是最短的），那么我们可以根据不同路口的车流量不同，对相应的小正方形赋予不同的权重；又例如，如果我们不想走高速，那么可以把高速路对应的小正方形的花销定义为无穷大……

为什么要采用我们介绍的方法求解

很容易想到的是，我们生活的世界如此庞大，“条条大路通罗马”，不可能枚举出所有的可能的路径，然后排个序，找到最短的。

甚至，就是对于上面抽象出的这个100×100的小正方形，其中存在的路径可能也太多了，即使在计算机的帮助下，枚举所有可能，然后找到最短路，这效率也非常低。

所以我们需要用到启发式算法、局部搜索算法。

启发式搜索是利用问题拥有的启发信息来引导搜索，达到减少搜索范围、降低问题复杂度的目的。

启发式搜索中，定义了一个评价函数对各个子结点进行计算，其目的就是用来估算出“有希望”的结点来。

要对OPEN表进行排序的时候，就按照这种“希望”进行排序。最有希望通向目标结点的待扩展结点会被优先扩展。

程序设计与算法分析

一般图搜索框架重塑

在这个问题中，采用的算法框架仍旧是一般图搜索框架，这在上一次作业《皇后问题》中已经给出了详细的算法说明和完整代码。

这里只简要重塑这个框架。

while (true) {
   
	if (open.isEmpty())
		return false;
	Node currentNode = open.poll();
	closed.add(currentNode);
	if (isTarget(currentNode)) {
   
		latest = currentNode;
		return true;
	}
	ArrayList<Node> m = expand(currentNode);
	if (m.isEmpty()) 
		continue;
	else 
		setPointer(m, currentNode);
}

需要修改的地方是设置父节点时候，要注意对OPEN表和CLOSED表的维护，其中对OPEN表排序需要按照启发式函数的评估值来排序。

由于每次都是评估值最小的排在最前面，所以其实可以在加入到OPEN表的时候就直接加入到恰当的位置，于是，OPEN表可以用优先级队列PriorityQueue来实现。

if (!open.contains(node) && !closed.contains(node)) {
   
	
} else if (open.contains(node)) {
   
	if (newDissipative < node.getDissipative()) {
   
		
	}
} else if (newDissipative < node.getDissipative()) {
   
	
}

数据存放形式与数据结构定义

• OPEN表：用于存放刚生成的节点

• CLOSED表：用于存放将要扩展或已扩展的节点

• Node：表示结点

• parent：指向父节点

数据域成员声明

• source：起点

• terminal：终点

• maze：地图，值为true表示可以通行，值为false表示这是障碍物

• result：最终找到的路径，以链表的形式返回

• progress：找路期间曾经试图访问过的点，以链表的形式返回

方法声明

/**
 * 评估函数的h(x)的值
 * @param source 起点
 * @param terminal 终点
 * @param parent 当前的点的父亲
 * @param node 当前的点
 * @return h(x)的值
 */
private double heuristic(Node source, Node terminal, Node parent, Node node) 

/**
 * 获得给定的点的邻居，邻居的定义是周围8个点
 * @param node 给定的点
 * @return 给定点的邻居
 */
private ArrayList<Node> getNeighbours(Node node) 

/**
 * 判断当前点是不是合法，合法的定义是不超过地图边界，且不是障碍物
 * @param x 横坐标
 * @param y 纵坐标
 * @return 如果合法，返回true，否则，false
 */
private boolean isValid(int x, int y) 

/**
 * 判断当前点是不是终点
 * @param node 当前点
 * @return 如果已经到了终点，返回true，否则，false
 */
private boolean isTarget(Node node) 

/**
 * 以链表的形式返回最终找到的路径
 * @return 最终找到的路径
 */
public LinkedList<Node> getResult() 

/**
 * 以链表的形式获得曾经试图访问过的点
 * @return 曾经试图访问过的点
 */
public LinkedList<Node> getProgress()

图形用户界面相关、交互相关

为了方便程序的调试，以及为了比较三种算法之间的优劣，我顺手写了图形用户界面。

因为这部分内容与本次作业的核心算法关系不大，所以下面不再详细给出这部分的数据定义、算法描述，只简要做出如下说明：

黑色：障碍，表示不能通过的地方

白色：道路，表示可以走的地方

红色：最终的路径

蓝色：曾经试图寻找的点，蓝色区域越大，说明搜索效率越低，找了那么多才找到这条路，蓝色区域越小说明搜索效率越高

算法

题目描述中有一些地方有歧义

为了更加清晰地表示下面的3种算法，做如下约定：

1．输入一定合法

不论是地图还是起点终点，输入的格式和数据一定合法，不存在非法数据或者错误格式。

2．下标从0开始

所描述的点，例如(5,4)表示的是第6行第5列。

3．8个方向是等价的

不存在“上、下、左、右”比“左上、左下、右上、右下”要优先的情况

4．走1步的花销定义为1

不论这一步是水平还是垂直走，还是斜着走，只要是走1步，花销就是1

从(0,0)走到(1,1)，是右下，这里花销不是$\sqrt{2}$，仍取1

5．从起点到终点的最优路线只看花销

只要花销是一样的，那么这几条路只是走法上的不同，在优劣程度上认为是一样

例如，下面2种走法，看作是等价的，区别只是走法的不同，而没有优劣之分，因为他们的花销都是5

起点	途径	途径	途径	途径	终点

****	途径	途径	****	****	****
起点	****	****	途径	途径	终点

最短路径算法

算法描述

首先看Dijkstra算法的描述：

这个算法是通过为每个顶点 v 保留目前为止所找到的从s到v的最短路径来工作的。初始时，原点 s 的路径权重被赋为 0 （d[s] = 0）。若对于顶点 s 存在能直接到达的边（s,m），则把d[m]设为w（s, m）,同时把所有其他（s不能直接到达的）顶点的路径长度设为无穷大，即表示我们不知道任何通向这些顶点的路径（对于所有顶点的集合 V 中的任意顶点 v， 若 v 不为 s 和上述 m 之一， d[v] = ∞）。当算法结束时，d[v] 中存储的便是从 s 到 v 的最短路径，或者如果路径不存在的话是无穷大。——该段引用自Wikipedia

那么就可以得到算法的主要思想。

首先从起点出发，试着往周围的8个点走，这时候这8个点都是1步就能到达的。之后，取这8个点的其中一个（因为这8个点距离起点都是1，所以都是最短的），继续找它的周围8个点，那么这些点的都是距离起点需要2步才能到达的。

每次都取待扩展的结点中，距离起点最短的结点往外扩展，这样搜索出来的路可以保证是最短路径。

在算法的实现过程中，如果一个点周围的8个点，有障碍物，或者已经超出了地图的边界，那么直接丢弃。

伪代码表示

于是，可以得到Dijkstra算法的伪代码描述。

对于图G中的每一个点V
初始化d[v] = Infinity，previous[v] = undefined   
d[s] = 0
S = empty
Q = 所有的V
while Q 非空
u = 取出(Q)中最小的点
把u加入到S
对于u能够走到的每一个v
if d[v] > d[u] + w(u,v)
d[v] = d[u] + w(u,v)，previous[v] = u

流程图

从这里可以看到，如果用一般图搜索框架来实现Dijkstra算法，用OPEN表存放所有的待扩展的结点，每次取出最小值，就是一个以当前“最短值”作为标准的优先级队列，而每次取出的u，相当于是更新父节点，并且维护OPEN表和CLOSED表。

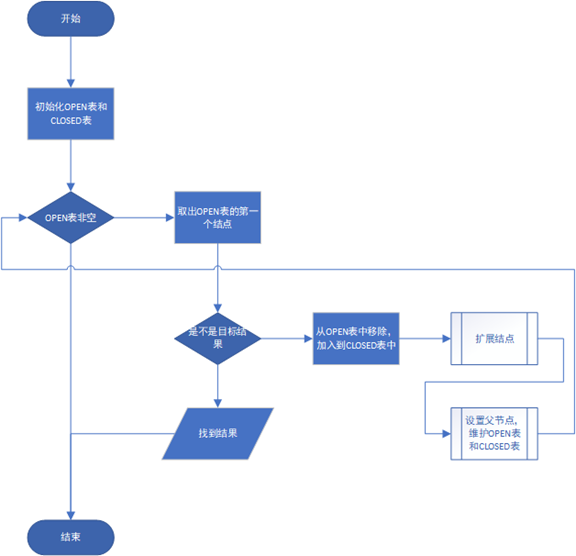
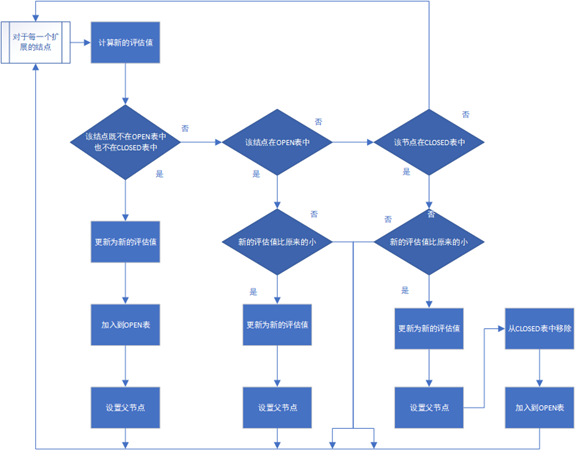
那么对于一般图搜索框架，需要修改以下部分。

for (Node node : m) {
   
	double newDissipative = 计算出新的评估值;
	if (!open.contains(node) && !closed.contains(node)) {
   
		node.setDissipative(newDissipative);
		open.add(node);
		node.setParent(parent);
	} else if (open.contains(node)) {
   
		if (newDissipative < node.getDissipative()) {
   
			node.setDissipative(newDissipative);
			node.setParent(parent);
		}
	} else if (newDissipative < node.getDissipative()) {
   
		node.setDissipative(newDissipative);
		node.setParent(parent);
		closed.remove(node);
		open.add(node);
	}
}

在这里，新的评估值就是 parent.getDissipative()+1。

A*算法

算法描述

启发式搜索算法A，一般简称为A算法，是一种典型的启发式搜索算法。

其基本思想是：定义一个评价函数f，对当前的搜索状态进行评估，找出一个最有希望的结点来扩展。

评价函数的形式如下：

$f(n)=g(n)+h(n)$当

在算法$A$的评价函数中，使用的启发函数$h(n)$是处在$h^{\ast }(n)$的下界范围，即满足$h(n)\le h^{\ast }(n)$时，则把这个算法称为算法$A^{\ast }$。

$A^{\ast }$算法实际上是分支界限和动态规划原理及使用下界范围的$h$相结合的算法。

首先令 g ( n ) g(n)