同态加密综述(一)

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

传统的加密系统依赖于在参与交换加密信息的对等人之间共享一个密钥（公共或私人）。然而，这种方法带来了隐私问题。拥有密钥的用户或服务提供商对数据有专属权利。特别是在流行的云服务中，对敏感数据的优先权的控制会丧失。即使在不共享密钥的情况下，加密的材料也会与不一定需要访问内容的第三方共享。此外，不受信任的服务器、供应商和云运营商可以在用户结束与服务的关系后，长期保留用户的识别要素。事实上，同态加密（HE），一种特殊的加密方案，可以解决这些问题，因为它允许任何第三方在不事先解密的情况下对加密数据进行操作。虽然HE方案的这一极其有用的特点已经存在了30多年，但第一个可信的、可实现的完全同态加密（FHE）方案是由Craig Gentry在2009年推出的，它允许任何可计算的函数在加密数据上执行。尽管这是一项重大成就，但迄今为止不同的实现方式表明，FHE仍然需要大幅改进才能在每个平台上实用。因此，本调查着重于HE和FHE方案。首先，我们介绍了HE的基础知识和著名的部分同态加密（PHE）和部分同态加密（SWHE）的细节，它们是实现FHE的重要支柱。然后，介绍了主要的FHE系列，它们已成为其他后续FHE方案的基础。此外，还调查了Gentry型FHE方案的实现和最近的改进。最后，讨论了进一步的研究方向。本调查旨在为有兴趣了解、应用和扩展最先进的HE、PHE、SWHE和FHE系统的研究人员和从业人员提供清晰的知识和基础。

---

一、介绍

1.1 同态

在抽象代数中，同态被定义为保留一个代数集的域和范围之间所有代数结构的映射。该映射只是一个函数，即一个操作，它从域的集合中获取输入，并在范围中输出一个元素（例如，加法，乘法）

1.2 同态加密（HE）

是一种加密方案，允许第三方（如云，服务提供商）在加密数据上执行某些可计算的功能，同时保留功能的特征和加密数据的格式。

1.3 传统加密方案的劣势

加密是保护任何敏感信息隐私的重要机制，然而，传统的加密方案不能在没有解密的情况下对加密的数据起作用。因此用户必须牺牲他们的隐私使用云服务器完成文件存储、共享或协作等操作。此外，不受信任的服务器、供应商和流行的云运营商可以在用户结束与服务的关系后，长期保留用户的物理识别元素

1.4 使用云服务器简单的同态加密实例

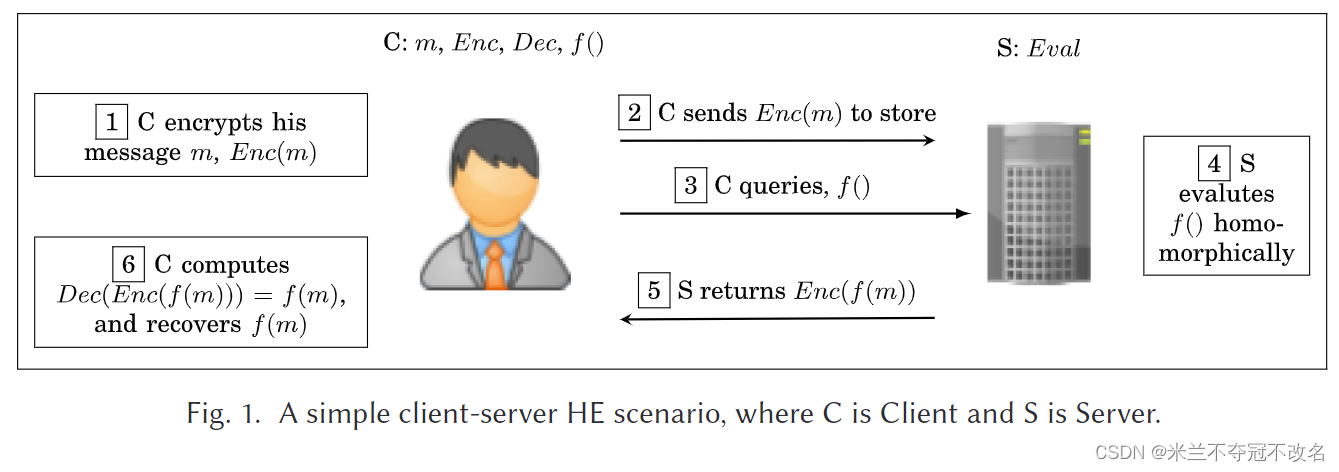
图1展示了一个简单的云计算应用实例。在这种情况下，客户C首先对他的私人数据进行加密（步骤1），然后将加密数据发送到云服务器S（步骤2）。当客户想要在他自己的数据上执行一个函数（即查询），f()，他将该函数发送到服务器（步骤3）。服务器使用Eval函数对加密数据进行同态操作，即蒙上眼睛计算f()（步骤4），并将加密的结果返回给客户（步骤5）。最后，客户用他自己的秘密密钥恢复数据，并获得sf(m)(步骤6)。从这个简单的例子中可以看出，服务器端的同态操作Eval()不需要客户端的私钥，并允许对加密的客户端数据进行各种操作，如加法和乘法。

1.5 同态加密的类型

• 部分同态加密(Partially Homomorphic Encryption，PHE)允许对密文进行一种类型的操作被执行无数次。(即对使用次数没有限制)。
  例如加法同态：Paillier算法，乘法同态：RSA算法
• 特定同态加密（Somewhat Homomorphic Encryption，SWHE) 允许对密文完成有限次的任意操作。（对操作没有限制，但是只能进行有限次）
• 完全同态加密（Fully Homomorphic Encryption，FHE）允许对密文进行无限次的任意操作。（操作和次数都没有限制）

二、同态加密方案

2.1 定义1

如果一个加密方案支持以下公式，则称其为操作 * 上的同态。
$$E(m_1)\ast E(m_2)=E(m_1\ast m_2),\forall m_1,m_2\in M$$
其中，$E$是加密算法，$M$是所有可能的信息集合。

2.2 HE的四个主要步骤

1. KeyGen：是为非对称版本的HE生成一对秘密和公共密钥的操作，或为对称版本生成一个单一的密钥。
2. Enc：加密
3. Dec：解密
   KeyGen、Enc和Dec与传统加密方案中的经典任务没有区别。
4. Eval：Eval是一个HE特有的操作，它将密码文本作为输入，并输出对应于一个函数的普通文本的密码文本。Eval在密码文本$(c_1,c_2)$上执行函数$f()$，而不看信息$(m_1,m_2)$。

三、Partially Homomorphic Encryption（PHE）方案

本节中描述了集中最基础，最中要的PHE算法，其他的算法基本都是基于这几种算法演化而来。

3.1 RSA

RSA是在1976年Diffie和Hellman发明公钥密码学后两年，由Rivest等人提出。RSA是公钥密码系统的第一个可行的研究成果（论文题目：‘ method for obtaining digital signatures and public-key cryp-tosystems’）。RSA密码系统的安全性是基于两个大素数乘积的因式分解问题的难易程度。定义如下：

• KeyGen算法：首先，对于大素数$p$和$q$，计算$n=pq$和$\varphi =(p-1)(q-1)$。然后。然后，选择 $e$ ，通过计算 $e$ 的乘法逆（即，$ed\equiv 1mod\varphi$）来计算 $gcd(e,\varphi )$ 和 $d$。（原文：Then,$e$ is chosen such that $gcd(e,\varphi )$ and $d$ are calculated by computing the multiplicative inverse of $e$(i.e.,$ed\equiv 1mod\varphi$).）最后，$(e,n)$作为公钥对被释放，而$(d,n)$作为私钥对被保存。

$gcd(a,b)$表示$a$和$b$的最大公约数

乘法逆元：
定义：若存在正整数a,b,p, 满足ab = 1(mod p), 则称a 是b 的乘法逆元, 或称b 是a 的乘法逆元。b ≡ a-1 (mod p)，a ≡ b-1 (mod p)
比如说, 在模7 意义下,3 的乘法逆元是5, 也可以说模7 意义下5的乘法逆元是3。模13意义下5的逆元是8
详解链接：http://t.zoukankan.com/mjtcn-p-7241896.html

• 加密算法：首先，将信息转换为明文m，使0≤m<n，然后采用RSA加密算法，如下所示，其中$c$是密文：
  $$c=E(m)=m^e(modn),\forall m\in M$$
• 解密算法：使用私钥对$(d,n)$可以从密码文本$c$中恢复信息$m$，如下所示：
  $$m=D(c)=c^d(modn)$$
• 同态属性：对于$m_1,m_2\in M$:
  $$E(m_1)\ast E(m_2)=(m_1^e(modn))\ast (m_2^e(modn))=(m_1\ast m_2{)}^e(modn)=E(m_1\ast m_2)$$

RSA的同态性表明，$E(m_1\ast m_2)$可以通过使用$E(m_1)$和$E(m_2)$直接评估，而无需解密。换句话说，RSA只对多乘法具有同态性。因此，它不允许密码文本的同态加法操作。

3.2 Goldwasser-Micali

Goldwasser和Micali（1982）提出了第一个概率性公钥加密方案GM。GM密码系统是基于二次剩余问题的难度（Kaliski2005）。如果存在一个整数$x$，使得$x^2\equiv a(modn)$，那么数字$a$就被称为二次剩余模$n$(quadratic residue modulo $n$)。二次残差问题决定了一个给定的数字q是否是模数n的二次方。GM密码系统描述如下。

• 密钥生成算法：与RSA类似，计算$n=pq$，其中$p$和$q$是不同的大素数，然后$x$被选为二次非保留模$n$值中的一个，$(\frac{x}{n})=1$（原文：then $x$ is chosen as one of the quadratic nonresidue modulo $n$ values with $(\frac{x}{n})=1$）。最后，$(x,n)$被公布为公钥，而$(p,q)$被保存为私钥。
• 加密算法：首先，消息$m$被转换成一串比特。然后，对于信息$m_i$的每一个比特，产生一个二次非保留值$y_i$，使得$gcd(y_i,n)=1$.然后，每个比特被加密为$c_i$，如下所示:
  c i = E ( m i ) = y i 2 x i m    ( m o d    n ) , ∀ m i = { 0 , 1 } c_i=E(m_i)=y^2_ix^m_i \; (mod \; n),\quad ∀m_i=\left\{0,1 \right\} ci​=E(mi​)=yi2​xim​(modn),∀mi​={0,1}
  其中$m=m_0{m}_1...m_r,c=c_0{c}_1...c_r$,$r$是用于信息空间的块大小，每次加密都从$Z_n^{\ast }$中随机挑选$x$，其中$Z_n^{\ast }$是整数模$n$的乘法子群，包括所有小于$r$且相对于$r$为素数的数字。
• 解密算法：由于$x$是从集合$Z_n^{\ast }(1<x\le n-1)$中挑选出来的，$x$是二次剩余模 $n$，只有$m_i=0$。因此，要解密密码文本$c_i$，就要决定$c_i$是否是二次剩余模 $n$；如果是，$m_i$返回$0$，否则$m_i$返回$1$。
• 同态特性：对于每个比特 m i ∈ { 0 , 1 } m_i∈\{0,1\} mi​∈{0,1}:
  $$\begin{gathered} E(m_1)\ast E(m_2)=(y_1^2{x}^{m_1}(modn))\ast (y_2^2{x}^{m_2}(modn)) \\ =(y_1\ast y_2{)}^2{x}^{m_1}+m_2(modn)=E(m_1+m_2) \end{gathered}$$

GM密码系统的同态性表明，和的加密$E(m_1\oplus m_2)$可以直接从单独的加密位$E(m_1)$和$E(m_2)$计算出来。由于信息和密码文本是集合 { 0 , 1 } \{0,1\} {0,1}的元素，操作与排他性OR（XOR）相同。因此，GM只对二进制数字的加法进行同构。

3.3 EL-Gamal

1985年，Taher Elgamal提出了一个新的公钥加密方案(ElGamal1985)，它是原来Diffie-Hellman Key Exchange(Diffieand Hellman1976)算法的改进版，它是基于离散对数中某些问题的难度(Kevin1990)。它多用于混合加密系统中，用于加密非对称加密系统的私钥。El-Gamal密码系统定义如下：

• KeyGen算法：使用生成器$g$产生一个具有$n$阶的循环组$G$。在一个循环组中，有可能使用其自身元素的幂来生成该组的所有元素。然后，对随机选择的$y\in Z_n^{\ast }$计算出$h=g^y$。最后，公钥是$(G,n,g,h)$，$x$是该计划的私钥。

• 加密算法：使用$g$和$x$对信息$m$进行加密，其中$x$是从 { 1 , 2 , . . . , n − 1 } \{1,2,...,n-1\} {1,2,...,n−1}集合中随机选择的，加密算法的输出是一对密码文本（$c=（c_1,c_2）$）:
  $$c=E(m)=(g^x,m{h}^x)=(g^x,m{G}^{xy})=(c_1,c_2)$$

• 解密算法：为了解密密码文本$c$，首先，计算$s=c_1^y$，其中$y$是私钥。然后，解密算法工作如下。
  $$c_2\cdot s^{-1}=m{g}^{xy}\cdot g^{-xy}=m$$

• 同态属性：
  $$E(m_1)\ast E(m_2)=(g^{x_1},m_1{h}^{x_1})\ast (g^{x_2},m_2{h}^{x_2})=(g^{x_1+x_2},m_1\ast m_2{h}^{x_1+x_2})=E(m_1\ast m_2)$$

从这个推导可以看出，El-Gamal密码系统是乘法同构的。它不支持对密码文本的加法操作。

3.4 Paillier

1999年，Paillier（1999）介绍了另一种基于复合残差问题的新型概率加密方案（Jager2012）。复合残差问题与GM和Benaloh密码系统中使用的二次和更高残差问题非常相似。它询问是否存在一个整数x，使xn≡a(modn2)为一个给定的整数a。

• KeyGen算法：对于大素数$p$和$q$，使$gcd(pq,(p-1)(q-1))=1$，计算$n=pq$和$\lambda =lcm(p-1,q-1)$。然后，通过检查$gcd(n,L(g^{\lambda mod{n}^2}))$是否$=1$来选择一个随机整数$g\in Z_{n^2}^{\ast }$，其中函数$L$被定义为$L(u)=(u-1)/n$，对于来自子组$Z_{n^2}^{\ast }$的每个$u$，它是一个整数模 $n^2$的乘法子组，而不是像Benaloh密码系统中的$n$。最后，公钥是$(n,g)$，秘钥是一对$(p,q)$。

• 加密算法：对于每个信息$m$，数字$r$是随机选择的，加密工作如下：
  $$c=E(m)=g^m{r}^n(mod{n}^2)$$

• 解密算法：对于一个适当的密码文本c<n2，解密的方法是:
  $$D(c)=\frac{L(c^{\lambda }(mod{n}^2))}{L(g^{\lambda }(mod{n}^2))}modn=m$$
  其中私钥对是(p,q)

• 同态属性：
  $$\begin{gathered} E(m_1)\ast E(m_2)=(g^{m_1}{r}_1^n(mod{n}^2))\ast (g^{m_2}{r}_2^n(mod{n}^2)) \\ =g^{m_1+m_2}(r_1\ast r_2{)}^n(mod{n}^2)=E(m_1+m_2) \end{gathered}$$

这一推导表明，Pailliler的加密方案对加法是同构的。除了对加法运算的同构性外，Pailliler的加密方案还有一些额外的同构性，它允许通过使用加密的明文$E(m_1)$和$E(m_2)$以及公钥对$(n,g)$对明文$m_1,m_2\in Z_{n^2}^{\ast }$进行额外的基本运算。
$$\begin{gathered} E(m_1)\ast E(m_2)(mod{n}^2)=E(m_1+m_2(modn)) \\ E(m_1)\ast g^{m_2}(mod{n}^2)=E(m_1+m_2(modn)) \\ E(m_1{)}^{m_2}(mod{n}^2)=E(m_1{m}_2(modn)) \end{gathered}$$

这些额外的同态属性描述了加密数据和明文的各种操作之间的不同交叉关系。换句话说，在以上三个公式中显示了在加密数据上计算的操作如何影响明文。

3.5 其他

此外，Okamoto-Uchiyama(OU)(Okamoto and Uchiyama 1998)提出了一个新的PHE方案，通过改变以前HE方案的加密集来提高计算性能。此外，NaccacheStern（NS）（Naccache和Stern1998）提出了另一个PHE方案，作为Benaloh密码系统的概括，以提高其计算效率。同样，Damgard-Jurik (DJ) (Damgård and Jurik 2001) 提出了另一个PHE方案，作为Paillier的概括。这三个密码系统保留了同态属性，同时改进了原有的同态方案。

同样，Kawachi（KTX）等人（2007年）提出了一个基于底层晶格问题硬度的大循环群的加法同态加密方案。他们把他们提出的方案的同态属性命名为假同态。伪同态是一种代数属性，仍然允许对密码文本进行同态操作；但是，对同态操作的密码文本的解密是以小的解密误差进行的。最后，Galbraith(2002)介绍了Paillier密码系统的一个更自然的概括，将其应用于椭圆曲线，同时仍然保留Paillier密码系统的同态属性。表1简要总结了著名的PHE方案的同态特性。

四、Somewhat Homomorphic Encryption(SWHE)方案

2009年之前的文献中有一些有用的SWHE例子（Yao1982；Sanderetal.1999；Boneh等人2005；Ishai和Paskin2007）。在2009年发表了第一个可信的FHE（Gentry 2009）之后，由于FHE方案的性能问题，一些SWHE版本的FHE方案也被提出。我们将这些SWHE方案放在FHE部分。在本节中，我们主要关注主要的SWHE方案，它们被用作第一个可信的FHE方案的垫脚石。

4.1 BGN

在2005年之前，所有提议的密码系统的同态性只限于加法或乘法运算，即SWHE方案。Boneh-Goh-Nissim(BGN)在Boneh等人(2005)中提出了走向FHE方案的最重要的步骤之一。BGN在密码文本上评估$2-DN{F}^5$公式，并通过保持密码文本大小不变，支持任意数量的加法和一个乘法。该方案的难点是基于子组决策问题（Gjøsteen2004）。子群决策问题只是决定一个元素是否是复合阶数$n=pq$的群$G_p$的子群的成员，其中$p$和$q$是不同的素数。

• KeyGen算法：公钥被发布为$(n,G,G_1,e,g,h)$。在公钥中，$e$是一个双线性映射，即$e:G\times G\to G1$，其中$G、G_1$是$n=q_1{q}_2$阶的群。$g$和$u$是$G$的生成器，设$h=u^{q_2}$，$h$是阶为$q_1$的$G$的生成器，作为私钥被隐藏起来。

• 加密算法：为了加密信息$m$，从集合 { 0 , 1 , . . . , n − 1 } \{0,1,...,n-1\} {0,1,...,n−1}中挑选一个随机数r，并使用预先计算的$g$和$h$进行加密，如下所示:
  $$c=E(m)=g^m{h}^{r}modn$$

• 解密算法：要解密密码文本$c$，首先要计算$c^{\prime }=c^{q_1}=(g^m{h}^r{)}^{q_1}=(g^{q_1}{)}^m$(注意$h^{q_1}\equiv 1modn$)和$g^{\prime }=g^{q_1}$，使用秘钥$q_1$完成解密，如下所示:
  $$m=D(c)=lo{g}_{g^{\prime }}{c}^{\prime }$$
  为了有效地解密，信息空间应保持小，因为离散对数不能快速计算。

• 同态加法：使用密码文本$E(m_1)=c_1$和$E(m_2)=c_2$对明文$m_1$和$m_2$进行同态加法，如下所示:
  $$c=c_1{c}_2{h}^r=(g^{m_1}{h}^{r_1})(g^{m_2}{h}^{r_2})h^r=g^{m_1+m+2}{h}^{r^{\prime }}$$
  其中$r=r_1+r_2+r$，可以看出，$m_1+m_2$可以很容易地从重新产生的密码文本$c$中恢复出来。

• 乘法的同态性：为了进行同态性的乘法，使用阶数为$n$的$g_1$和阶数为$q_1$的$h_1$，并设置$g_1=e(g,g),h_1=e(g,h)$,和$h=g^{\alpha q_2}$.然后，使用密码$c_1=E(m_1)$和$c_2=E(m_2)$对信息$m_1$和$m_2$进行同态性的乘法计算如下。
  $$\begin{gathered} c=e(c_1,c_2)h_1^r=e(g^{m_1}{h}^{r_1},g^{m_2}{h}^{r_2})h_1^r \\ =g_1^{m_1{m}_2}{h}_1^{m_1{r}_2+r_2{m}_1+\alpha q_2{r}_1{r}_2+r}=g_1^{m_1{m}_2}{h}_1^{r^{\prime }} \end{gathered}$$
  可以看出，$r^{\prime }$和$r$一样是均匀分布的，所以$m_1{m}_2$可以正确地从结果密码文$c$中恢复出来。然而，$c$现在是在组$G_1$中，而不是在$G$中。他们的协议在协议复杂度方面比Yao(1982)中著名的乱码电路协议有了四倍的改进。

4.2 其他

在HE方案的文献中，最早的SWHE方案之一是PollyCracker方案（Fellows和Koblitz1994）。它允许对密码文进行乘法和加法运算。然而，密码文本的大小随着同构操作的进行而呈指数级增长，而乘法操作尤其极其昂贵。后来提出了更有效的变体（Levy-dit Vehel和Perret 2004；VanLy 2006），但几乎所有的变体后来都被证明容易受到攻击（Steinwandt 2010；Levy-dit Vehel et al.2009）。因此，它们要么是不安全的，要么是不切实际的（Le2003）。最近，Albrecht等人（2011年）引入了一个带噪声的Polly Cracker加密系统，其中同态加法运算不增加密码文的大小，而乘法运算则使其平方。

另一个对加密数据进行评估操作的想法是在不同的集合上实现的。Sander,Young和Yung(SYY)描述了第一个在半群上的SWHE方案，NC1,6(Sander等人，1999)，它需要比群更少的属性。NC1是一个复杂性类别，包括具有多项式深度和多项式尺寸的电路。所提出的方案支持用一个OR/NOT门对密码文进行多项ANDing。然而，密码文的大小随着每个OR/NOT门的评估而以恒定的倍数增加。这种增加限制了对电路深度的评估。Yuval Ishai和Anat Paskin(IP)将这组程序扩展到分支程序(又称二进制决策图)，这是一个有向无环图，其中每个节点都有两条标有二进制0和1的出线(Ishai and Paskin 2007)。换句话说，他们通过评估加密数据的分支程序提出了一个公开密钥加密方案。此外，Melchor等人（2010）提出了一个通用的构建方法，以获得一个链式加密方案，允许对密码文本的恒定深度电路进行同态评估。该链式加密方案是由具有一些同态特性的知名加密方案获得的。例如，他们展示了如何获得BGN（Boneh et al.2005）和Kawachi et al.（2007）的组合。如前所述，BGN允许任意数量的加法和一个乘法，而Kawachi的方案只具有加法同构性。因此，由此产生的组合方案允许任意的加法和两个乘法。他们还展示了如何将这一程序应用于Melchor等人（2008）的方案，允许预定数量的同态加法，以获得一个允许任意数量乘法的方案。然而，在乘法中，密码文本的大小呈指数级增长，而在同态加法中则是恒定的。如表2所示，在Yao、SYY和IP密码系统中，密码文本的大小随着每次同态操作而增长；而在BGN中，它保持不变。BGN的这一特性是获得FHE方案的一个重大改进。因此，Gentry、Halevi和Vaikuntanathan后来简化了BGN密码系统（Gentry et al.2010）。在他们的版本中，基本的安全假设被改变为LWE问题的硬性。BGN密码系统从一个小的集合中选择输入以正确解密。相比之下，Gentryet al.(2010)介绍的最新方案有更大的信息空间。此外，一些试图获得基于SWHE方案的FHE方案的尝试被报道为被破坏。例如，Mullenand Shiue (1994), i Ferrer (1996), Grigoriev and Ponomarenko (2006), and Domingo-Ferrer (2002)的漏洞分别在Steinwandt and Geiselmann (2002), Choi et al. (2007), Wagner (2003) and Cheonet al. (2006)报告。

---