习题集解析部分
第1章 绪论
——《数据结构习题集》-严蔚敏.吴伟民版
源码使用说明 链接☛☛☛《数据结构》(严蔚敏,吴伟民版)课本源码+习题集解析使用说明
课本源码合辑 链接☛☛☛《数据结构》课本源码合辑
本文档所在目录:数据结构\▼配套习题解析\▼01 绪论\
习题解析
一、基础知识题
1.1❶ 简述下列术语:数据、数据元素、数据对象、数据结构、存储结构、数据类型和抽象数据类型。
1.2❷ 试描述数据结构和抽象数据类型的概念与程序设计语言中数据类型概念的区别。
1.3❷ 设有数据结构(D,R),其中
D={d1,d2,d3,d4},R={r},r={(d1,d2),(d2,d3),(d3,d4)}。
试按图论中图的画法惯例画出其逻辑结构图。
1.4❷ 试仿照三元组的抽象数据类型分别写出抽象数据类型复数和有理数的定义(有理数是其分子、分母均为自然数且分母不为零的分数)。
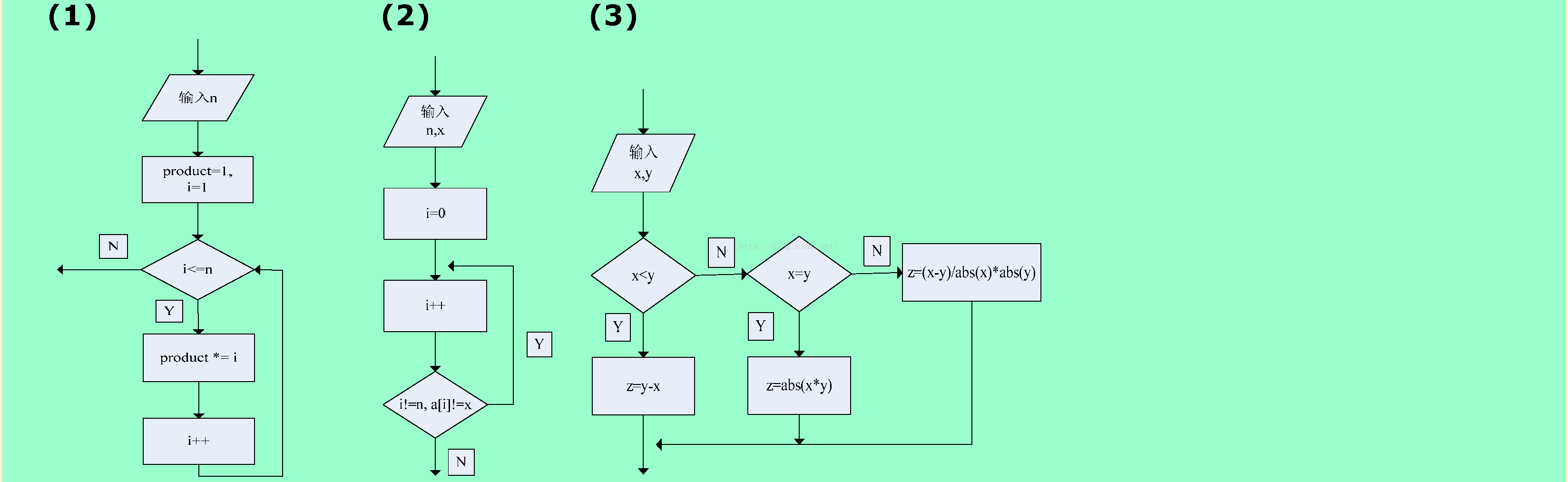
1.5❷ 试画出与下列程序段等价的框图。
(1)product = 1;
i = 1;
while(i<=n)
{
product *= i;
i++;
}
(2)i=0;
do
{
i++;
}while((i!=n) && (a[i]!=x));
(3)switch
{
case x<y: z=y-x;
break;
case x==y: z=abs(x*y);
break;
default: z=(x-y)/abs(x)*abs(y);
}
1.6❸ 在程序设计中,常用下列三种不同的出错处理方式:
(1)用exit语句终止执行并报告错误;
(2)以函数的返回值区别正确返回或错误返回;
(3)设置一个整型变量的函数参数以区别正确返回或某种错误返回。
试讨论这三种方法各自的优缺点。
1.7❸ 在程序设计中,可采用下列三种方法实现输出和输入:
(1)通过scanf和printf语句;
(2)通过函数的参数显式传递;
(3)通过全局变量隐式传递。
试讨论这三种方法的优缺点。
1.8❹ 设n为正整数。试确定下列各程序段中前置以记号@的语句的频度:
(1)i = 1; k = 0;
while(i <= n-1)
{
@ k += 10 * i;
i++;
}
(2)i = 1; k =0;
do
{
@ k += 10 * i;
i++;
}while(i <= n-1);
(3)i = 1; k =0;
while(i <= n-1)
{
i++;
@ k +=10 * i;
}
(4)k = 0;
for(i=1; i<=n; i++)
{
for(j=i; j<=n; j++)
@ k++;
}
(5)for(i=1; i<=n; i++)
for(j=1; j<=i; j++)
for(k=1; k<=j; k++)
@ x += 1;
(6)i = 1; j = 0;
while(i+j <= n)
{
@ if(i>j)
j++;
else
i++;
}
(7)x = n; y = 0; //n是不小于1的常数
while(x >= (y+1)*(y+1))
@ y++;
(8)x = 91; y = 100;
while(y>0)
{
@ if(x>100)
{
x -= 10;
y--;
}
else
x++ ;
}
1.9❸ 假设n为2的乘幂,并且n>2,试求下列算法的时间复杂度及变量count的值(以n的函数形式表示)。
int Time (int n)
{
count = 0;
x = 2;
while(x<n/2)
{
x *= 2;
count++;
}
return (count)
}//Time
1.10❷ 按增长率由小至大的顺序排列下列各函数:
2100,(3/2)n,(2/3)n,(4/3)n,nn,n3/2,n2/3,√n,n!,n,log2n,n/log2n,log22n,log2(log2n),nlog2n,nlog2n
各函数的排列次序如下:
1.11❸ 已知有实现同一功能的两个算法,其时间复杂度分别为O(2n)和O(n10),假设现实计算机可连续运算的时间为107秒(100多天),又每秒可执行基本操作(根据这些操作来估算算法时间复杂度)105次。试问在此条件下,这两个算法可解问题的规模(即n值的范围)各为多少?哪个算法更适宜?请说明理由。
1.12❸ 设有以下三个函数:
f(n)=21n4+n2+1000,g(n)=15n4+500n2,h(n)=5000n3.5+nlogn
请判断以下断言正确与否:
(1)f(n)是O(g(n))
(2)h(n)是O(f(n))
(3)g(n)是O(h(n))
(4)h(n)是O(n3.5)
(5)h(n)是O(nlogn)
1.13❸ 试设定若干n值,比较两函数n2和50nlog2n的增长趋势,并确定n在什么范围内时n2的值大于50nlog2n。
1.14❸ 判断下列各对函数f(n)和g(n),当n→∞时,哪个函数增长更快?
1.15❸ 试用数学归纳法证明:
二、算法设计题
1.16❷ 试写一算法,自大到小依次输出顺序读入的三个整数X,Y和Z的值。
完整源码见 ☛《数据结构习题集》-第1章-绪论-第1.16题
1.17❸ 已知k阶斐波那契序列的定义为
f0=0, f1=0, …, fk-2=0,fk-1=1;
fn=fn-1+fn-2+…+fn-k,n=k,k+1,…
试编写求k阶斐波那契序列的第m项值的函数算法,k和m均以值调用的形式在函数参数表中出现。
完整源码见 ☛ 《数据结构习题集》-第1章-绪论-第1.17题
1.18❸ 假设有A、B、C、D、E五个高等院校进行田径对抗赛,各院校的单项成绩均已存入计算机,并构成一张表,表中每一行的形式为
| 项目名称 | 性别 | 校名 | 成绩 | 得分 |
编写算法,处理上述表格,以统计各院校的男、女总分和团体总分,并输出。
1.19❹ 试编写算法,计算i!*2i的值并存入数组a[0..arrsize-1]的第i-1个分量中(i=1,2,…,n)。假设计算机中允许的整数最大值为maxint,则当n>arrsize或对某个k(1≤k≤n)使k!*2k>maxint时,应按出错处理。注意选择你认为较好的出错处理方法。
完整源码见 ☛ 《数据结构习题集》-第1章-绪论-第1.19题
1.20❹ 试编写算法求一元多项式的值Pn(x),并确定算法中每一语句的执行次数和整个算法的时间复杂度。注意选择你认为较好的输入和输出方法。本题的输入为ai(i=0,1,…,n),x0和n,输出为Pn(x0)。
完整源码见 ☛ 《数据结构习题集》-第1章-绪论-第1.20题
更多章节持续更新中...





 本解析涵盖《数据结构》严蔚敏版习题集第一章基础知识题,深入解答数据结构概念、算法设计与分析等问题。
本解析涵盖《数据结构》严蔚敏版习题集第一章基础知识题,深入解答数据结构概念、算法设计与分析等问题。


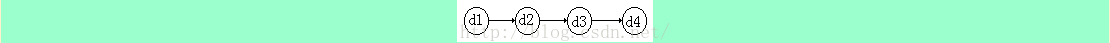




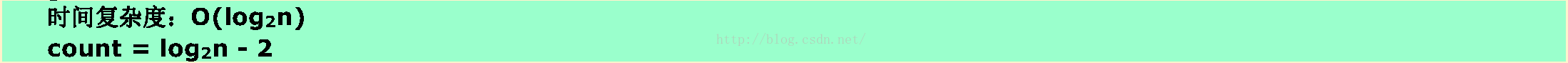




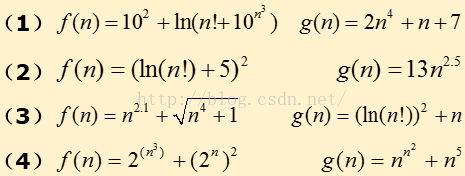
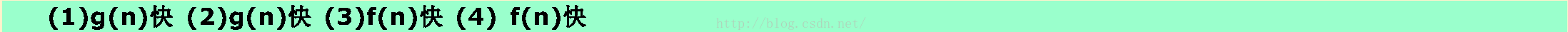
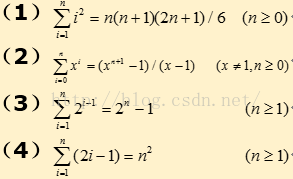






















 1416
1416

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








