sporadic偶发实时任务多核分区动态优先级EDF（或者DM）调度（以及可调度性分析）经典算法详解

我是标同学

已于 2022-06-03 17:15:44 修改

阅读量2.1k

点赞数 3

分类专栏：多核调度文章标签： EDF可调度性分析算法多核分区EDF调度 EDF调度任务分配方法

于 2022-05-31 17:58:51 首次发布

本文链接：https://blog.csdn.net/kangkanglhb88008/article/details/125058802

版权

多核调度专栏收录该内容

12 篇文章

订阅专栏

sporadic任务的概念：实时任务分类与术语_标biao的博客-CSDN博客，也就是任务的截止期可以小于周期。

with no loss of generality，任务集为封闭任务集，不会运行时动态加入任务，因此所有任务信息已知。那么整个算法步骤如下：

确定任务分配的顺序：比如是按照利用率降序排序，还是截止期大小排序，等等，可以有多种排序方式
如何分配核，也就是挑选核的顺序：比如按照FF,NF,WF,BF等多核实时调度—任务分配启发式算法解读FF,NF,BF,WF_标biao的博客-CSDN博客
确定了目标核后，就是每个核上采用什么调度策略：比如RM，DM，还是动态优先级EDF
确定了任务，确定了核，现在如何知道该任务在此核可不可行了，即采用的可调度性测试算法

分区EDF调度

我们从上面链接文章中可以知道，其实 FFD的可调度性是最好的，那么一下子我们就确定好了第一和第二步了（第一步是按照截止期从小到大顺序分配任务的）。由于EDF是单处理器当的最优调度算法，无论是periodic任务还是sporadic任务（有文献可查），因此，当然选EDF调度啦（理想情况，不考虑运行时开销。但是实际情况中用固定任务优先级调度RM和DM的多，但我觉得EDF未尝不可）。

然后就剩下一步，sporadic任务在一个核上是否可调度的可调度性分析问题了。我们知道periodic任务（截止期等于周期的任务）在EDF调度下的可调度性测试就是总利用率小于1即可。但是sporadic任务可不一样了，它的可调度性测试时间复杂度很高，所以用了充分性测试算法2（附录2）。该算法的名字叫做 PARTION()，伪代码如下：来自论文（The Partitioned Multiprocessor Scheduling of Sporadic Task Systems）

该分配算法的时间复杂度：

$\huge DBF^{(1)}(\tau_j,t)$ 的计算时间复杂度为 $\huge O(i+m)$ ，这里指当前任务的序号为 i ，因此分配完所有任务的时间复杂度为 $\huge \sum_{i=1}^{n}O(i+m)$ ，它的时间复杂度是 $\huge {\color{Red} O(n^2)}$ ，其中 $\huge m \le n$ ，m表示处理器核数，n表示任务集任务数。

分区DM调度

如果每个核采用DM调度，（截止期也需要从小到大顺序分配任务的），那么只需要将上面伪代码的第3行的可调度性判定条件改一下即可，书上用的是RBF*（P111页，很好理解，这里就不啰嗦了），来自论文（The Partitioned Scheduling of Sporadic Tasks According to Static-Priorities，2006年），算法名字叫做 FBB-FFD。我觉得这个其实还可以用更精确的，这篇论文中提出了多种，大家可以看看（Partitioned Multiprocessor Fixed-Priority Scheduling of Sporadic Real-Time Tasks, 2016年），我还能提出另一种更精确的，后续写篇论文，说说这个算法。

时间复杂度同上面一样： $\huge {\color{Red} O(n^2)}$

附录（单核中的EDF调度可调度性测试发展）：

下面这个图来自（Fixed-Priority Schedulability of Sporadic Tasks on Uniprocessors is NP-hard）

任务模型（ci, di, pi）

精确的EDF可调度性测试算法：需要在任务集所有周期最小公倍数内Q < lcm{p1,p2,... ,pn}（因为最小公倍数表示调度再次重来了），每个时刻是否都能满足所有任务（这里说作业，更为准确）的执行量需求（下面为什么是求和形式呢，因为EDF不像固定优先级调度，EDF是根据截止期的动态优先级，所以当前作业是可能被所有其它作业干扰的），如下：（EDF-schedulability of synchronous periodic task systems is coNP-hard）

上面这个很明显是NP-hard复杂度（准确来说是 (weakly) co-NPhard，据说是NP-hard问题的补集问题，

论文【EDF在单核中，约束截止期和任意截止期sporadic任务的精确可调度性分析时coNP-hard“Edf-schedulability of synchronous periodic task systems is conp-hard】

，虽然具体区别没有深入了解，但是可以肯定的是不是多项式时间复杂度）。这里举个sporadic任务EDF调度，可调度性测试的例子：

上述没有多项式复杂度求解，是因为需要遍历所有的Q值，这个可能太多了。

这里，我们拆开来看，单独定义为如下函数 需求上界函数DBF，如下：任务模型符号改一下（Ci, Di, Ti）

$\huge \forall Q \geq 0, \sum_{i=1}^{n}DBF(\tau_i,Q) \le Q$

这个本质是什么呢，就是任务i，的作业们到达时刻和截止时刻都得包含在区间 t 内的作业的执行量请求。因为现在是EDF调度呀（截止期），所以截止期不在分析区间中，就代表它优先级还不够高(和固定优先级调度的本质区别)，可能没有执行。而对于固定优先级调度而言，就不同了，只要高优先级作业的到达时间包含在区间里就可以了（和该作业的Di在不在没有关系），就会产生干扰量，用的就是最坏干扰时间方法(但是该方法仅仅是充分性的可调度性测试，因此有carry in job)，简单转换就能知道 $\huge DBF(\tau_j,t) \le I(\tau_j,t)$ 。（这两个计算都是没有更高优先级抢占时的最大执行量，其实有没有更高优先级都没有关系（我们可以用忙用期间策略证明的），我们不需要担心）如下公式： $\huge I(\tau_j,t)=\left \lfloor {\frac{t}{T_j}} \right \rfloor *C_j+min{\{C_j, t \mod T_j\}}$

DBF()函数也很好理解，就是扣除一个Di（因为Di总能认为是一个必要的，产生1个Ci执行量），看看剩下的还有几个完整的Ci嘛。

EDF的可调度性测试那个公式，其实跟固定优先级调度的分析方法RTA是类似（回想RTA的迭代过程），这个遍历上面的所有Q点，实际上就是类似于计算这些点的响应时间。这也难怪固定优先级调度的精确可调度性分析是NP-hard时间复杂度的证明过程，就是通过将固定优先级调度的精确分析先后RTA（里面用的是RBF请求上界函数，待会会讲）等价起来，然后，多项式时间规约到这个EDF的测试算法（已知道为NP-hard）中来呢（Fixed-Priority Schedulability of Sporadic Tasks on Uniprocessors is NP-Hard，Static-priority Real-time Scheduling: Response Time Computation is NP-hard）

由于精确EDF测试需要测试的时刻点太多了，运行时间开销太大。因此有人（Efficient Feasibility Analysis for Real-Time Systems with EDF scheduling）提出，一方面，其实DBF的值不是每个时刻点都会发生变化（从上面的例子也可以看出来），那么我们只需要测试这些会发生变化的时刻点即可（很明显就是那些截止期除以周期整数倍的时刻这样子的点），但是这个好像每人提出过这个想法，如果想做，应该可以发个论文。另一方面可以没必要测试到最小公倍数那儿去，Igerge即为需要测试的最大时刻点，如下：（Efficient Feasibility Analysis for Real-Time Systems with EDF scheduling）其实跟响应时间分析RTA的不断提高测试效率是一样的发展过程。

EDF调度精确的可调度性测试方法无论怎么改进，还是到不了真正的多项式时间复杂度（那肯定，因为EDF-schedulability of synchronous periodic task systems is coNP-hard证明过了EDF调度的可精确调度性测试是NP-hard的），所以大家就去研究近似测试算法（也就是充分性的，不是充要的），这样就能达到多项式时间复杂度了。

知识1：EDF调度中，任务集中任务提前按照截止期从小到达排序了，那么可调度性测试时候就是逐个任务往后测试即可（如果不排序，那就只能用上面说的精确可调度性测试了）。这个特性，很神奇（因为按道理说EDF是动态优先级，大截止期的任务也可能会干扰小截止期任务的呀，这个在下面的文章中应该能找到证明过程，我没有深究了，默认了），这一点跟固定优先级任务调度时候很像。下面的充分性（近似）测试算法就是利用了这个特性。

知识2：EDF调度中，最坏情况，也是所有任务同时释放的时刻，这个特性和固定优先级调度也一样了，也很神奇，我没有深究了，默认了。

第一个EDF充分性可调度性测试算法：An Improved Schedulability Test for Uniprocessor Periodic Task Systems。可以看出这个算法的时间复杂度为O(n^2)，n为任务集的任务数。

第二个EDF充分性可调度性测试算法：大家觉得DBF()不太可能在多项式时间计算出来（这个不就是直接可以算出来吗？因此我也不太认同，但是也没有深究了），所以对它进行了近似，结果如下：

原理就是用直线去近似DBF()这个阶梯函数了（这样计算起来确实会快），其中k表示想要保留的阶梯数（相当于通过k来指定想要的近似精度），其它的阶梯都被近似了，效果如下：

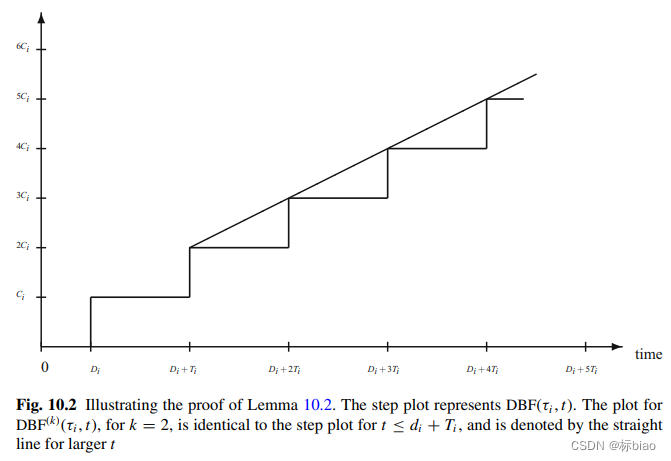
所以可调度性测试算法的最终结果如下：（这个也是需要任务集按照截止期从小到达排序了的，然后逐个任务往后测试，测试任务i，需要同时满足的两个不等式如下（其中， $\huge \tau(k)$ 表示已测试过的任务的集合，每测试完一个任务就会往这个集合添加进去），因此整个任务集可调度性测试时间复杂度也为O(n^2)，n为任务集的任务数）

上面11.4式是用来测试截止期大于周期时候的任务的。？11.3式为什么这样就能充分性判定EDF可调度性了，我也没想清楚，这样岂不是和固定优先级调度时候一样的测试行为了，后面再来深究一下这个，原论文其实也有证明，大家可以看看（The Partitioned Multiprocessor Scheduling of Sporadic Task Systems）