机器学习（二）——朴素贝叶斯(NB)模型

1 基础知识

1.1 条件概率

条件概率是指我们感兴趣的事一件事先发生作为前提下，发生的概率。给定事件B在事件A发生的前提下发生的概率记为P(B|A)：
$$P(B|A)=\frac{P(A,B)}{P(A)}$$
其中P(A,B)表示A、B同时发生的概率，P(A)表示A事件发生的概率。

1.2 贝叶斯规则

我们经常会需要在已知P(A|B)的情况下求P(B|A)。例如医生知道某种病存在什么症状，但是在诊断时，医生是根据病人出现的症状确定患者得了什么病。幸运的是如果此时我们还直到P(A)的话，我们就可以根据贝叶斯规则来实现这一目的：
$$P(A|B)=\frac{P(A)P(B|A)}{P(B)}$$
而P(B)又可以根据链式法则求得:
$$P(B)=\sum _{a\in A}P(B|a)P(a)$$
则贝叶斯公式最终可写为：
$$P(A|B)=\frac{P(A)P(B|A)}{{\sum }_{a\in A}P(B|a)P(a)}$$

1.3 贝叶斯决策

假设在一个分类任务中有N种标记类别，记为 y = { c 1 , c 2 , c 3 , . . . , c n } \bm{y}=\{c_{1},c_{2},c_{3},...,c_{n}\} y={c1​,c2​,c3​,...,cn​}，有M个样本，记为 x = { x 1 , x 2 , x 3 , . . . , x m } \bm{x}=\{x_{1},x_{2},x_{3},...,x_{m}\} x={x1​,x2​,x3​,...,xm​}。在机器学习中就是要学得一个模型(这里我们设模型要学习的参数为$\theta$)，尽可能准确的估计出样本的后验概率$P(c|\mathbf{x})$。此时有两种方法：通过直接建模$P(c|\mathbf{x})$来预测$c$，这样的到的是“判别式模型”，有决策树、BP神经网络、支持向量机等；另一种方法是先对联合概率分布$P(\mathbf{x},c)$建模，然后再获得$P(c|\mathbf{x})$，这样是“生成式模型”。对于生成式模型：
$$P(c|\mathbf{x})=\frac{P(\mathbf{x},c)}{p(\mathbf{x})}=\frac{P(c)P(\mathbf{x}|c)}{P(\mathbf{x})}$$
其中$P(c)$是类先验概率；$P(\mathbf{x}|c)$是样本$\mathbf{x}$相对于类标记$c$的类条件概率；$P(\mathbf{x})$是用于归一化的”证据“因子。因此估计$P(c|\mathbf{x})$的问题就转化为基于训练数据来估计先验概率$P(c)$和$P(\mathbf{x}|c)$。
贝叶斯决策的判定准则为最小化总体风险。在这里我们用${\lambda }_{ij}$表示将真实的$c_j$类误分为$c_i$所产生的损失，基于后验概率$P(c_i|\mathbf{x})$可以求得将样本$\mathbf{x}$分类为$c_i$的期望损失：
$$R(c_i|\mathbf{x})=\sum _{j=1}^N{\lambda }_{ij}P(c_j|\mathbf{x})$$
对每个样本如果$R(c_i|\mathbf{x})$能优化到最小，那么总体的风险$R(h)$也将被最小化。因此贝叶斯判定准则表示为：为最小化总体的风险，只需在每个样本选择那个能使条件风$R(c|\mathbf{x})$最小的类别标记，即
$$h^{\ast }(\mathbf{x})=\underset{c\in \mathbf{y}}{\mathrm{argmax}}R(c|\mathbf{x})$$
$h^{\ast }(\mathbf{x})$被称为贝叶斯最优分类器，与之对应的总体风险$R(h^{\ast })=\mathbb{E}(R(h^{\ast }(\mathbf{x})|\mathbf{x})$，$1-h^{\ast }(\mathbf{x})$为分类器所能达到的最好性能，即分类模型的模型精度的理论上限。

1.4 朴素贝叶斯分类器

计算贝叶斯后验概率的最大困难在于类条件概率$P(\mathbf{x}|c)$是所有属性上的联合概率，很难从有限的训练样本进行直接估计。为了解决这个问题，朴素贝叶斯引入了”属性条件独立假设“：对所有已知类别，假设所有属性相互独立，即每个属性独立的影响分类结果。因此后验概率公式可写为：
$$P(c|\mathbf{x})=\frac{P(c)P(\mathbf{x}|c)}{P(\mathbf{x})}=\frac{P(c)}{P(\mathbf{x})}\prod _{i=1}^{d}P(x_i|c)$$
其中$d$为属性数目，$x_i$为$\mathbf{x}$在第$i$个属性上的取值。
由于对所有类别来说$P(\mathbf{x})$都相同，因此朴素贝叶斯分类器的判别准则可以写为：
$$h_{NB}(\mathbf{x})=\underset{c\in \mathbf{y}}{\mathrm{argmax}}P(c)\prod _{i=1}^{d}P(x_i|c).$$
因此朴素贝叶斯分类器的训练过程就是根据训练集估计先验概率$P(c)$，并为每个属性估计类条件概率$P({\mathbf{x}}_i|c)$
1）对于先验概率$P(c)$，如果$D_c$表示第$c$类样本集合，在有充足独立同分布样本的情况下：
$$P(c)=\frac{|D_c|}{|D|}$$
2)对于类条件概率$P({\mathbf{x}}_i|c)$，需要分属性是连续还是离散。
（1）对于离散属性，用$D_{c,x_i}$表示$D_c$中第$i$个属性上取值为$x_i$的样本的集合，那么：
$$P({\mathbf{x}}_i|c)=\frac{|D_{c,x_i}|}{|D|}$$
（2）对连续属性，假定$p({\mathbf{x}}_i|c)$服从均值为${\mu }_{c,i}$方差为${\sigma }_{c,i}^2$的分布，其中${\mu }_{c,i}$和${\sigma }_{c,i}^2$是第$c$类样本在第$i$个属性上的均值和方差，那么：
$$p(x_i|c)=\frac{1}{\sqrt{2\pi {\sigma }_{c,i}^2}}exp\left(-\frac{(x_i-{\mu }_{c,i}{)}^2}{2{\sigma }_{c,i}^2}\right)$$

2 代码实践

2.1 高斯朴素贝叶斯(连续变量)

我们使用鸢尾花数据集进行NB模型的探索。鸢尾花数据集一共包含5个变量，其中4个特征变量，1个目标分类变量。共有150个样本，目标变量为花的类别 其都属于鸢尾属下的三个亚属，分别是山鸢尾 (Iris-setosa)，变色鸢尾(Iris-versicolor)和维吉尼亚鸢尾(Iris-virginica)。包含的三种鸢尾花的四个特征，分别是花萼长度(cm)、花萼宽度(cm)、花瓣长度(cm)、花瓣宽度(cm)，这些形态特征在过去被用来识别物种。

变量	描述
sepal length	花萼长度(cm)
sepal width	花萼宽度(cm)
petal length	花瓣长度(cm)
petal width	花瓣宽度(cm)

target 鸢尾的三个亚属类别

类别	数量
‘setosa’(0)	50
‘versicolor’(1)	50
‘virginica’(2)	50

导入数据，特征数据放入X，标签数据放入y，并划分训练集和测试集：

X, y = datasets.load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

接下来就是根据训练数据获得所需的两个先验概率了：类别先验概率$P(Y=c_k)$和$P(X^{(i)}=x^{(i)}|Y=c_k)$。
我们先假设目前数据的四个特征都符合高斯分布，那么就可选择高斯朴素贝叶斯进行分类。
我们把一个服从均值为$\mu$方差为${\sigma }^2$的数据称为服从高斯分布，我们可以使用每个特征的均值来估计$\mu$，使用所有特征的方差来估计${\sigma }^2$。
$$P(X^{(i)}=x^{(i)}|Y=c_k)=\frac{1}{\sqrt{2\pi {\sigma }_y^2}}exp\left(-\frac{(x^{(i)}-{\mu }_{ck}{)}^2}{2{\sigma }_{ck}^2}\right)$$

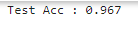
from sklearn.naive_bayes import GaussianNB

clf = GaussianNB(var_smoothing=1e-8)
clf.fit(X_train, y_train)

得到训练模型后对测试数据进行预测：

y_pred = clf.predict(X_test)
acc = np.sum(y_test == y_pred) / X_test.shape[0]
print("Test Acc : %.3f" % acc)

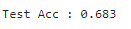
2.1贝叶斯分类(模拟离散型变量)

这里生成离散的数据进行模拟，随机生成600个100维的数据，每一维的特征都是[0, 4]之前的整数，即该数据有600个样本，100个不同的属性，各属性值是[0,4]之间的离散值。标签为[1,2,3,4,5,6]共6类。由此构成data，前100维为特征，最后一维为标签。

# 模拟数据
rng = np.random.RandomState(1)
# 随机生成600个100维的数据，每一维的特征都是[0, 4]之前的整数
X = rng.randint(5, size=(600, 100))
y = np.array([1, 2, 3, 4, 5, 6] * 100)
data = np.c_[X, y]

然后对数据乱序，同时划分训练集和测试集

# X和y进行整体打散
random.shuffle(data)
X = data[:,:-1]
y = data[:, -1]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

接下来使用基于类目特征的朴素贝叶斯模型进行学习

from sklearn.naive_bayes import GaussianNB

clf = CategoricalNB(alpha=1)
clf.fit(X_train, y_train)
acc = clf.score(X_test, y_test)
print("Test Acc : %.3f" % acc)