原文标题:Multi-Column Deep Neural Network for Traffic Sign Classification(2012)
作者:Dan Ciresan, Ueli Meier, Jonathan Masci and Jurgen Schmidhuber
这片文章描述的是参加 The German Traffic Sign Recognition Benchmark (http://benchmark.ini.rub.de/?section=gtsrb&subsection=news)比赛的一个算法,最终赢得了该比赛的第一名。
本文是对该文章主要内容的部分翻译,并补充了一些个人观点,如有问题或者疑问,欢迎指出。
摘要:
在Traffic Sign Classification中,文中方法能达到99.46%的准确率,是唯一 一个优于人类识别(human recognition)率的算法。每个单独的DNN都无需人工提取特征,而是 learned in a supervised way。最后将多种 trained on differently preprocessed data 的DNNs 结合(combine)到一个MCDNN,进一步提高了识别性能和泛化能力。
1.简介:
目前最成功的 分层物体识别系统(hierarchical object recognition systems)都是针对输入图像提取局部特征,然后用滤波器卷积图像块。Filter responses are then repeatedly pooled and re-filtered, 由此产生了一个深度前馈网络结构,其输出的特征向量用于最后的分类。
应用到原始图像块的无监督学习方法,一般是产生局部滤波器(localized filters),比如:off -center-on-surround filters, orientationsensitive bar detectors, Gabor filters.在使用中,这些滤波器的权值是固定的(fixed)。
相比之下,卷及神经网络(CNNs)的滤波器的权重是随机初始化的,使用BP算法有监督学习。
单个DNN—MCDNN的基本构建模块,是一个多层的神经网络结构,结构中 convolutional层和max-pooling层交替出现。
Meier (2011)指出,多个不同DNN的结合无需优化,只需 averaging 输出结果,在unseen test set 中也有不错的效果,具有很好的泛化能力。
实验的快速实现依赖于GPUs, fully online (i.e., weight updates after each image)。训练一个大型的DNN仅需要几天的时间,而不是几个月。
The German traffic sign recognition benchmark (GTSRB),是一个43类的分类问题,包括两个阶段,初步评估阶段和现场总结赛阶段。
初步评估阶段,我们使用了一组多层感知器(MLP:Multi-Layer Perceptrons) trained on provided features 和一个DNN trained on raw pixel intensities,即MLP+DNN。
本文描述的是现场总结赛阶段所使用的方法,MCDNN。
2.MCDNN
作为MCDNN的基本构建模块,DNN交替使用converlution层和max-pooling层。
2.1DNN
一个DNN包括一系列的converlution层和max-pooling层,每一层只连接前一层。它是一种常见的、多层的特征提取器,将输入图像的原始像素密度映射为一个特征向量,然后使用2~3层的全连接层对特征向量进行分类。所有可调参数通过最小化训练集的误分类误差(through minimization of the misclassification error)得到调整和优化。
2.1.1卷积层
图1a:DNN结构
每个卷积层执行一次2D的卷积,执行对象为:层所有输入图像 和 一个size为
的滤波器。
层的所有输入图像的最终激活值(resulting activations)是
层所有卷积响应的和,可以通过相面的一个非线性激活函数得到:
公式中各参数的意义:
n :层数
Y :图片,大小为
:滤波器,大小为

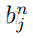
*: valid 2D convolution
对于输入图片:size为
, 滤波器
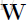
,
输出图像
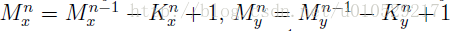
注意:公式1遍历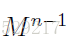
2.1.2 Max-pooling层
文章中提到:DNN和CNN最大的区别是:CNN使用的是sub-sampling层,而DNN使用的是max-pooling层。两者均可以认为是 池化 的过程。
采样层:是对上一层map的一个采样处理,这里的采样方式是对上一层map的相邻小区域进行聚合统计,区域大小为scale*scale,
有些实现是取scale*scale小区域的最大值,即max-pooling。
有些实现是采用scale*scale小区域的均值,即sub-sampling。
注意,卷积的计算窗口是可以重叠的。本文采用的计算窗口没有重叠。
2.1.3分类层
卷积层卷积核的大小和max-pooling层矩形区域的大小 的设定一般需满足:最后一层卷积层的输出maps正好降维到1个pixel per map,或者,使用一个全连接层将最后一层卷积层的所有输出 combine into 一个1维的特征向量。在分类任务中,最后一层一般是全连接层,每一个输出节点代表一类。
本文中,最后一层使用softmax 激励函数,从而可以把每个节点的输出看作是每一类出现的概率。
softmax function:归一化一组值到0~1之间,总和为1。换句话说,是一种归一化操作,是的输出在(0,1)之间。
2.1.4训练单个DNN
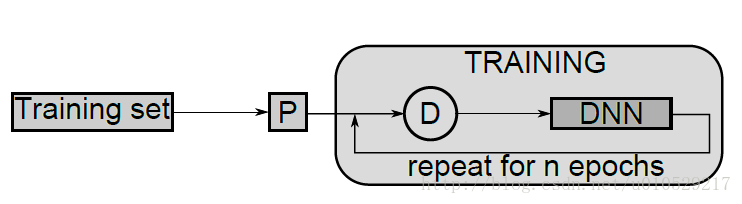
图1b:训练单个DNN:在训练开始前,给定的数据集先进行预处理(P:preprocessed),
然后训练过程中,每个epoch前,all original or preprocessed images随机失真(D:distorted)。
注意:预处理过程不是随机的,训练前,整个数据集都需要进行统一的或特定的预处理。(3.1会详细介绍)
失真处理是随机的(此处的‘随机’是指处理方式是随机的),在训练过程中,失真处理每一张预处理过的图片
输入图像经过预处理,并在训练过程中不断被扭曲。图像预处理不是随机的,图像扭曲是随机的,应用在每一个预处理图像的训练过程中,使用随机的有界值进行位移,旋转和尺度变换。这些值在特定的范围均匀分布,图像位移在正负10%的范围,尺度变换在0.9—1.1,旋转范围在正负5度。最终固定尺寸图像是通过扭曲输入图像双线性插值得到。
图像扭曲是为了用很多自由参数训练DNN时避免过拟合,大大改善识别性能。
all DNN training:在线(online)梯度下降,退火学习率(学习率逐渐降低)。
2.1.5 MCDNN的形成
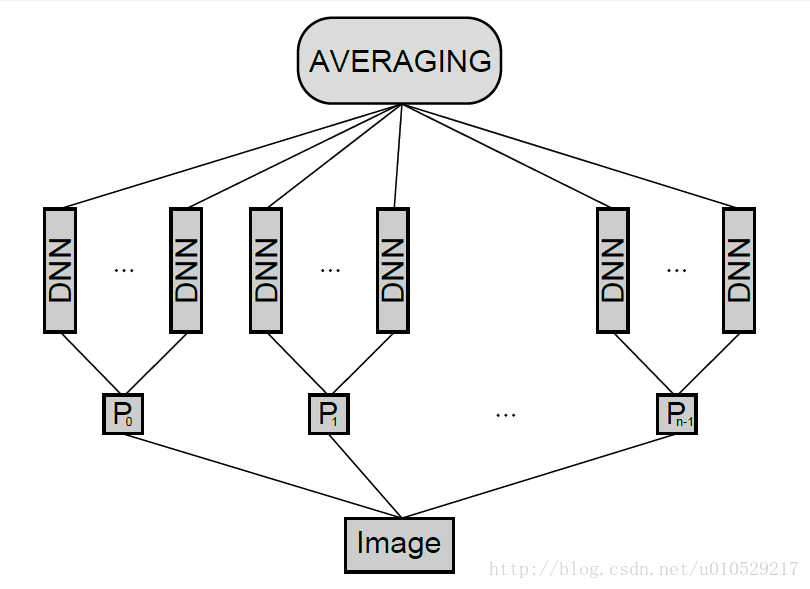
图1c:MCDNN 结构:The input image is preprocessed by n different preprocessors P0 — Pn-1,
and an arbitrary number of columns is trained on each preprocessed input.
The final predictions are obtained by averaging individual predictions of each DNN.
平均多个不同的DNN列的输出激励,组建一个MCDNN。对于一个给定的输入模型,对所有列的预测值平均化。训练前,所有列的权重随机初始化。
Various columns can be trained on the same inputs, or on inputs preprocessed in different ways。(谨记:相同不相同是针对‘P’而言)
事实上,使用相同的数据集训练的模型的误差具有高度的相关性。为了避免这个问题,我们的MCDNN结合了不同归一化(产生多种不同的数据集)数据训练的多种DNN。一个关键的问题是:多个模型的输出结果在combination时,需不需要进行优化(即:是对DNNs的结果直接average,还是加个weight)。
训练中常见的问题有两个:1)需要附加的训练集(本文通过 'D' 过程解决);2)无法保证的是:训练后的MCDNN对未知的训练集也能产生较好的结果。(即:泛化能力有待商榷)。
对于手写数字,Meier文章中指出,对于测试集,仅仅对多个DNN的输出结果进行平均化,要比对多个DNN进行线性组合(linear combination)(权重通过验证集得到优化)具有更好的泛化能力。因此,本文中直接averaging the outputs of each DNN。
这里的average怎么理解呢?
假如有两个DNNs,每个DNN 的输出节点有4个,(即4类)。
假设:第一个DNN 输出结果为:0.3,0.1,0.5,0.1;第二个DNN输出结果为:0.5,0.2,0.1,0.2,所以MCDNN的average输出为:0.4,0.15,0.3,0.15。所以最终结果说明,输入图像属于第一类。(这里的概率均为假设,纯属为计算方便,一般实际的概率输出差别会比较大)
(纯属个人观点,如有不同意见,欢迎共享)
3.实验
使用的系统:1个Core i7-950 (3.33GHz), 24 GB DDR3, 4个 graphics cards of type GTX 580.
training set 中,只有未变形的、原始的或者预处理过的图像才被用于验证过程,当验证误差为0(一般需要15~30 epochs)时,结束训练过程。
初始权重(卷积核的权重)从范围为 [-0.05,0.05] 的均匀随机分布中获取。每个神经元的激励函数为双曲正切函数。
3.1 数据预处理
每一幅原始彩色图片内包含一个交通图标,图标周围有10%的边界(border)。原始彩色图片大小从15*15到250*250不等,且一般不为正方形。在图片中,交通图标一般不居中,边界框(bounding box)是注释(annotations)的一部分。
训练集一共39209幅图像,测试集为12630幅图像。
preprocessing:
- '切割'(crop)所有的图像,并且只处理边界框(bounding box)内的图片。MCDNN要求所有的训练图像必须为正方形。本文中resize所有的图像大小为 48*48 pixels。Resizing forces them to have square bounding boxes。
- 对比度归一化。文中使用了4种对比度归一化方法:Image Adjustment (Imadjust),Histogram Equalization (Histeq),Adaptive Histogram Equalization (Adapthisteq),Contrast Normalization (Conorm)。(图像调整,直方图均衡化,自适应直方图均衡化,对比度归一化)
Image Adjustment (Imadjust):通过映射像素强度到新的值,增加图像的对比度,比如将1%的数据渗透到低强度和高强度。
Histogram Equalization (Histeq):直方图均衡化,转换像素强度增强对比度;输出图像直方图大致均衡统一。 “中心思想”是把原始图像的灰度直方图从比较集中的某个灰度区间变成在全部灰度范围内的均匀分布。利用图像直方图对对比度进行调整,这种方法通常用来增加许多图像的局部对比度,尤其是当图像的有用数据的对比度相当接近的时候。通过这种方法,亮度可以更好地在直方图上分布。这样就可以用于增强局部的对比度而不影响整体的对比度,直方图均衡化通过有效地扩展常用的亮度来实现这种功能。
Adaptive Histogram Equalization (Adapthisteq):AHE算法通过计算图像的局部直方图,然后重新分布亮度来来改变图像对比度。该算法更适合于改进图像的局部对比度以及获得更多的图像细节。图像分为8个6*6不重叠的区域,每一块直方图大致均衡统一来增强图像对比度。
注意:HE是全局的,AHE是局部的。
Contrast Normalization (Conorm):通过高斯差分滤波增强图像边缘。本文中使用的滤波器的size为 5*5 pixels。
需要注意的是:除了Contrast Normalization (Conorm),其余的3种归一化方法不是在RGB-color space中实现的,而是在一个图像强度作为它的一个成分的彩色空间里。因此,先将图像从 RGB space转换到 Lab-space,进行归一化处理,然后再将归一化后的图像转换到 RGB space。
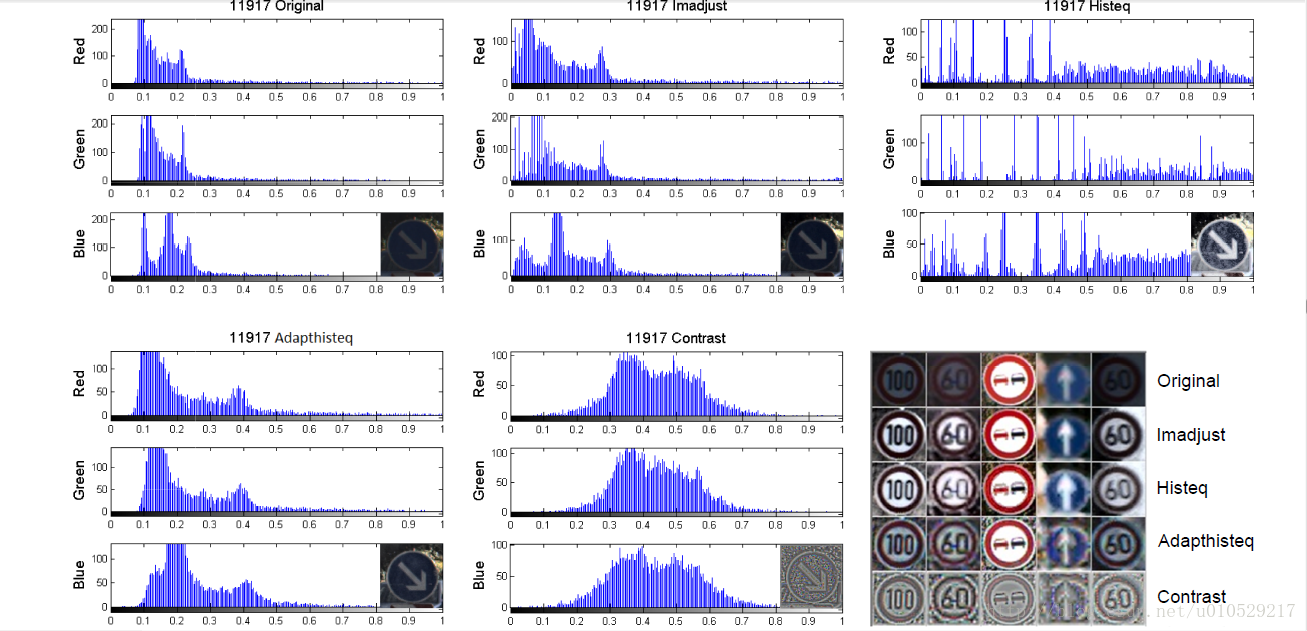
四种不同的归一化方法的效果如图2所示,包括了原始图像和归一化图像的像素密度直方图。
图2:Histogram of pixel intensities for image 11917 from the test set of the preliminary
phase of the competition, before and after normalization, as well as an additional selection
of 5 traffic signs before and after normalization
3.2实验结果
初始实验证明深度网络要比浅层网络的工作效果好。
本文中使用的单个DNN为9层,具体信息如 table1:
相同的结构在figure 3也有所体现,figure 3 表示的是所有层的 the activations 和 the filters (已经训练的DNN)。
figure 3:DNN architecture from Table 1 together with all the activations and the learned
fi lters. Only a subset of all the maps and fi lters are shown, the output layer is not drawn
to scale and weights of fully connected layers are not displayed. For better contrast, the
fi lters are individually normalized.
第一层的滤波器用彩色表示,需注意的是,该彩色滤波器原则上包括三个独立的滤波器,分别连接到输入图片的 red channel、green channel 和 blue channel。
The input layer has three maps of 48x48 pixels for each color channel ; the output layer consists of 43 neurons, one per class.
总体结构共有1.5million个参数,一半的参数来源于最后两层的全连接层。
使用4个GPUs,训练25列的MCDNN,需要37hours。训练以后,单个的GPU每秒能够处理87幅图像。
文章中也使用了 15*15的滤波器代替7*7的滤波器,They are randomly initialized, and learn to respond to blobs(斑点), edges and other shapes in the input images。第一卷积层的滤波器如 figure4:
figure4:The learned filters of the first convolutional layer of a DNN.
The layer has 100 maps each connected to the three color channels of the input image for a total of 3x100 filters of size 15x15.
Every displayed filter is the superposition(叠加) of the 3 filters that are connected to the red, green and blue channel of the input image respectively.
For better contrast, the filters are individually normalized.
总体:
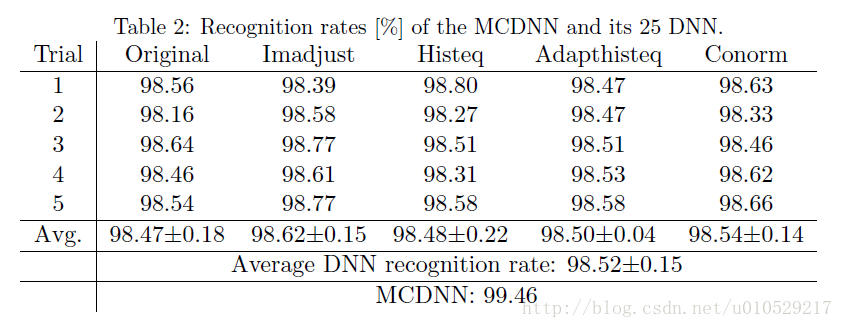
训练了25个DNN,每5个DNN对应一种 P(包括原始图像和4种归一化方法),即:每个P连接5列DNN。实验结果如表2所示:
table 2中,trial 横向代表5种P,纵向的数字(1,2,3,4,5)代表DNN的‘序号’(每个P有5个DNNs)。
实验结果中,Average DNN recognition rate 为 98.52%,而MCDNNrecognition rate为99.46%,如果说MCDNN的最终输出结果为所有DNN的average,为什么两者不相等呢?为什么MCDNN的结果优于Average DNN呢?
请教过别人后理解是,每个DNN都有自己的识别率即准确率,该准确率是通过训练多幅图像所得。而MCDNN 只需要一幅图像,average所有DNN的输出结果即可。table显示的是每个DNN的最优识别率,而MCDNN得到的是 所有DNN平均值 的最优识别率(可能某个DNN 没有达到自己的最好状态,出现分类错误的情况),两者没有直接的关系。(感觉有些矛盾,对不对!)因为MCDNN是多个DNN的结合,总体上还是会比单个DNN 的结果要好一些。
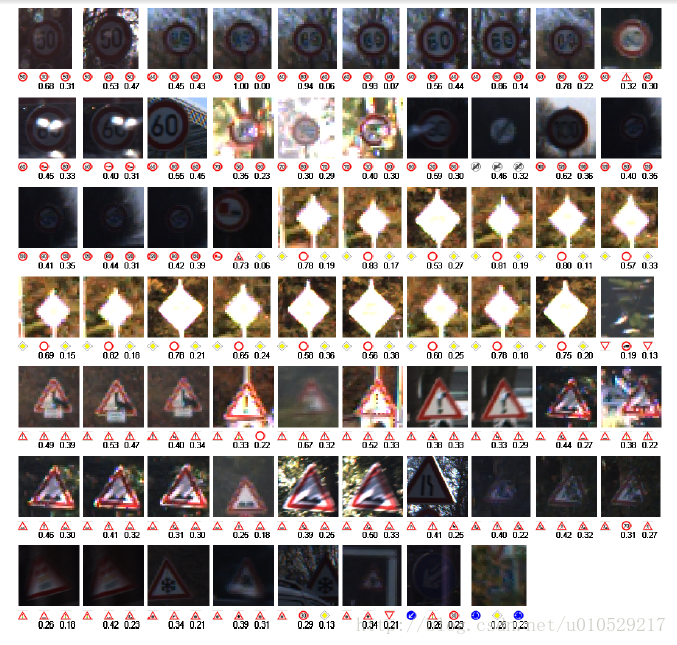
figure 5 显示了所有错误,还有真实值、第一次预测、第二册预测。68个错误中,超过80%的错误都在第二次预测中得到正确结果,Erroneously predicted class probabilities tend to be very low—here the MCDNN is quite unsure about its classifications。不过,一般来说,MCDNN的预测概率值要么接近于1,要么接近于0,这一点是毋庸置疑的。
figure 5:The 68 errors of the MCDNN, with correct label (left) and first(middle) and
second best (right) predictions. Best seen in color.
Rejecting only 1% percent of all images (con dence below 0.51) results in an even lower error rate of 0.24%. To reach an error rate of 0.01% (a single misclassi cation), only 6.67% of the images have to be rejected (con fidence below 0.94).
4.总结:
参考:http://tech.ddvip.com/2014-08/1408423169212655.html
http://www.cnblogs.com/Imageshop/archive/2013/04/07/3006334.html
http://wenku.baidu.com/linkurl=P5Ah1iKgfTtmH9DDi83CkmQHWvDOdnP6dOQrSVlDrWT_HZ04Gd7wIAsF2lF_AXyJ59TBPUnkBtQsF1FAfZ4bAtZbz4AJc35eQ_nDprr5Cxy










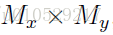



















 2891
2891

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








