【LeetCode】141、环形链表

【声明】

如果有侵权，请联系作者删除侵权部分。

如果有错误，请联系作者修改错误部分。

如果有转载，请标明出处。

【难度】

简单

【题目】

给定一个链表，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪next指针再次到达，则链表中存在环，为了表示给定链表中的环，我们使用整数pos来表示链表尾连接到链表中的位置（索引从0开始）。如果pos是-1，则在该链表中没有环。注意：pos不作为参数进行传递，仅仅是为了标识链表的实际情况。

如果链表中存在环，则返回true。否则，返回false。

进阶：

你能用O(1)（即，常量）内存解决此问题吗？

【示例】

【示例1】

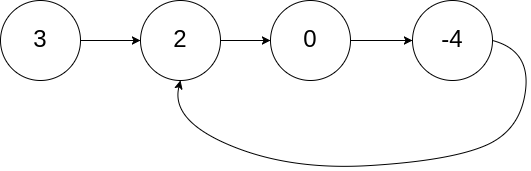
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

【示例2】

输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

【示例3】

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

【题目链接】

https://leetcode-cn.com/problems/linked-list-cycle/

【解题思路】

       如果一个链表中有环，那么遍历整个链表，必然会有节点被访问两次。因此可以对已经访问过的节点进行记录，访问当前节点的next节点时，先判断该节点是否曾经被访问过，如果被访问过，则证明链表中有环。如果直到链表结束，都没有访问到已经访问过的节点，则证明链表中不存在环。该方法可借助hash表来实现。

       另一种方法是采用快慢指针。如果链表中不存在环，那么就类似于在单向道路上行进，总会走到路的终点。如果链表中存在环，那么就类似于在环形道路上行进。在环形道路中，如果有两个人在行进，一个人走的快，另一个人走的慢，那么这两个人必定会在某时刻相遇。因此，判断链表中是否存在环，可以采用这个办法。定义两个指针，一个快指针，一个慢指针，快指针每次走两步，慢指针每次走一步，如果快指针先到达终点，则该链表不存在环，如果快慢指针相遇，则说明链表中存在环。

【代码】

//hash表法
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        unordered_set<ListNode*> us;
        while (head != nullptr) {
            if (us.find(head) == us.end()) {
                us.insert(head);
                head = head->next;
            }
            else {
                return true;
            }
        }
        return false;
    }
};

//快慢指针法
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        ListNode* slow = head;
        ListNode* fast = head;
        while (fast != nullptr) {  //快指针未到终点
            slow = slow->next;
            fast = fast->next;
            if (fast != nullptr) {  //快指针走两步
                fast = fast->next;
            }
            else {
                return false;
            }
            if (slow == fast) {    //快慢指针相遇
                return true;
            }
        }
        return false;
    }
};

【心得】

        发现题目的规律非常重要，虽然暴力解法也可以解决问题，但是相比更好的解法，时间复杂度和空间复杂度可能会差一些。要有追求最优解法的心。