【洛谷 P5787】二分图 线段树分治【二分图】【线段树分治】

---

解题思路

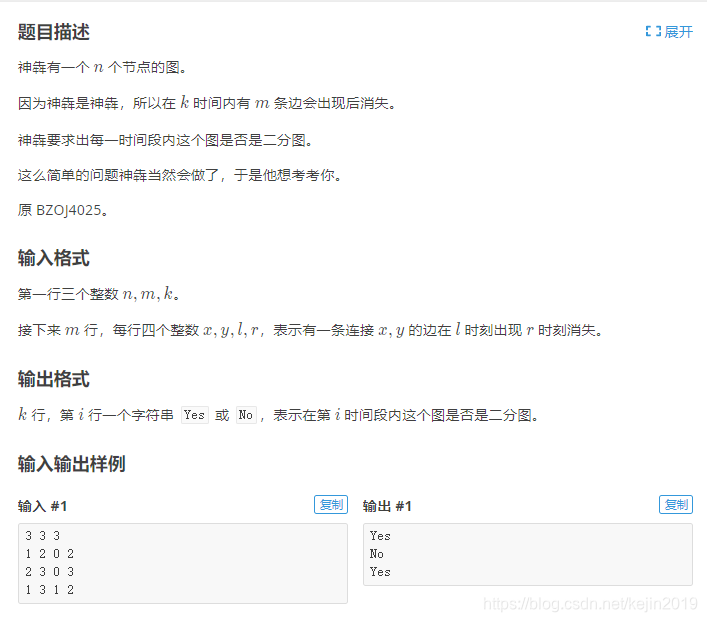
题目大意：一张图有 n 个节点的图， 在 k 时间中会出现 m 条边，表示有一条连接 x,y 的边在 l 时刻出现 r 时刻消失，求问在第 i 个时间段中图是否为二分图。

先对于二分图来分析：

如果顶点 V 可分割为两个互不相交的子集 (A,B) ，并且图中的每条边 (i,j)所关联的两个顶点 i 和 j 分别属于这两个不同的顶点集 (i∈A,j∈B) ，则称图 G 为一个二分图。 —— 百度百科。

• 在一般的做法中对于一个图是否为二分图，我们一般是采用染色法，如果一个图为二分图，那么一条边所连接的两个点一定是在不同集合的，也就是点的颜色不同。

这个方法时间复杂度和空间复杂度都必须优化。
我们知道图是二分图的充要条件是不存在奇环，这个可以用到一个叫扩展域并查集的东西维护

• 扩展域并查集：对于一个节点$i$，我们将其拆分为两个节点$（i，i+n）$。一个属于集合 S ，另一个属于集合 T 。把$i$和$j$相连，就把$（i，j+n），（j，i+n）$连在一起。因为一条边所连接的两个节点就必须在不同的集合中，所以，当本应该在 $S$ 中的$i$点和在 T 中$i+n$点在一个集合中了，那么这张图就不是二分图。
  例子：假设$i$和$j$相连，则把$（i，j+n），（j，i+n）$连在一起（使用并查集让它们属于一个集合），再让k和j相连，则把$（k，j+n），（j，k+n）$连在一起。现在$（i，j+n，k）$属于一个集合，$（i+n，j，k+n）$属于一个集合。
  如果现在连接$i，k$，即把$（i，k+n），（k，i+n）$连在一起就会让（i，j+n，k，k+n）属于一个集合，$（i+n，j，k+n，k）$属于一个集合。发现本应该在 $S$ 中的$k$点和在 T 中$k+n$点在一个集合中了，那么这张图就不是二分图。

对于时间段分析
我们把时间轴画出来，那么对于每一条边它总是在时间轴上覆盖了一些区域。所以对于一条边我们可以将其分解。

我们先将时间轴构建 logk 层，然后就像插入区间一样，把每一条边插入。因为对于线段树上的一个节点，它的子节点也一定被这条边覆盖，那么我们只需要在父亲节点储存这条边。那么这样对于一条边最大也只会分解为 logk 不重复的较小的边。

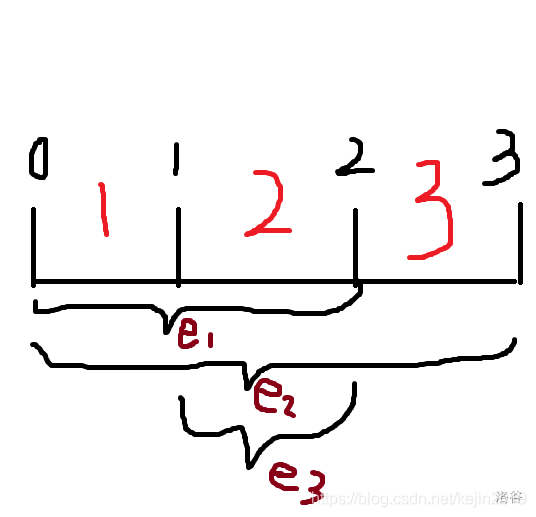
这样我们把所有边在线段树上映射好，最后一次性处理线段树的所有叶子结点（因为区间总长k，要输出对应k个时间段）。但是我们发现当我们处理完一个节点的子节点后，我们必须将这个节点对应的时间新增的边删掉，将并查集还原到处理之前的状态才可以递归处理其他节点。

删边处理方法：我们可以把所有操作放在栈里，当我们退出时，撤销原操作就行了。
但是这样我们就不可以路径压缩了，因为每个节点是要储存他真正的父亲的。为了保证复杂度的正确性，必须要按秩合并。将树的深度大的合并到深度小的的父亲下面，这样树的高度是不会高于 $O(\log n)$ 的。

总结：建一个时间轴上的线段树，再通过并查集维护答案。

---

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<iomanip>
#include<cstring>
#include<cmath>
#include<map>
#include<queue>
#include<set>
#define ll long long
#define ldb long double
using namespace std;

int n,m,k,x,y,l,r,top;
int fa[400010],h[400010];

struct c {
	int x,y;
} a[400010];

struct Stack {
	int x,y,v;
} st[400010];

vector<int>t[1000100];

void up(int dep,int l,int r,int x,int y,int v) {
//	if(l>y||r<x)return;
	if(x<=l&&y>=r) {
		t[dep].push_back(v);
		return;
	}
	int mid=(l+r)/2;
	if(x<=mid)up(dep*2,l,mid,x,y,v);
	if(y>mid)up(dep*2+1,mid+1,r,x,y,v);
}

int find(int x) {
	if(fa[x]==x)return fa[x];
	return find(fa[x]);
}

void add(int x,int y) {
	int fx=find(x),fy=find(y);
	if(h[fx]>h[fy])swap(fx,fy);
	st[++top]=(Stack) {
		fx,fy,h[fx]==h[fy]
	};
	fa[fx]=fy;
	if(h[fx]==h[fy])
		h[fy]++;
}

void work(int dep,int l,int r) {
	int lasttop=top,ok=0;
	for(int i=0; i<t[dep].size(); i++) {
		int aa=find(a[t[dep].at(i)].x);
		int bb=find(a[t[dep].at(i)].y);
		if(aa==bb) {
			for(int j=l; j<=r; j++)
				printf("No\n");
			ok=1;
			break;
		}
		add(a[t[dep].at(i)].x,a[t[dep].at(i)].y+n);
		add(a[t[dep].at(i)].x+n,a[t[dep].at(i)].y);
	}
	if(!ok) {
		if(l==r)printf("Yes\n");
		else {
			int mid=(l+r)>>1;
			work(dep*2,l,mid);
			work(dep*2+1,mid+1,r);
		}
	}
	while(top>lasttop) {
		h[fa[st[top].x]]-=st[top].v;
		fa[st[top].x]=st[top].x;
		top--;
	}
	return;
}

int main() {
	scanf("%d%d%d",&n,&m,&k);
	for(int i=1; i<=m; i++) {
		scanf("%d%d%d%d",&a[i].x,&a[i].y,&l,&r);
		up(1,1,k,l+1,r,i);
	}
	for(int i=1; i<=2*n; i++)
		fa[i]=i,h[i]=1;
	work(1,1,k);
}