二叉树遍历的非递归实现
相对于递归遍历二叉树,非递归遍历显得复杂了许多,但换来的好处是算法的时间效率有了提高。下面对于我学习非递归遍历二叉树算法的过程进行总结
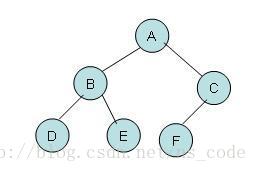
为了便于理解,这里以下图的二叉树为例,分析二叉树的三种遍历方式的实现过程。
一.非递归实现二叉树的前序遍历
不借助递归,要实现二叉树的前序遍历,我们需要用到前面学过的栈这种数据结构。根据前序遍历的定义,先访问根节点,再访问左子树,最后访问右子树。声明指向节点的指针pCur,我们可以先访问根节点,之后让根节点进栈,并让pCur在左子树上移动直到pCur为空时,令栈顶元素出栈,让pCur在栈顶元素的右子树上继续移动即可
用自然语言描述为:
对于任一节点P,
1)输出节点P,然后将其入栈,再看P的左孩子是否为空;
2)若P的左孩子不为空,则置P的左孩子为当前节点,重复1)的操作;
3)若P的左孩子为空,则将栈顶节点出栈,但不输出,并将出栈节点的右孩子置为当前节点,看其是否为空;
4)若不为空,则循环至1)操作;
5)如果为空,则继续出栈,但不输出,同时将出栈节点的右孩子置为当前节点,看其是否为空,重复4)和5)操作;
6)直到当前节点P为NULL并且栈空,遍历结束。
下面以上图为例详细分析其先序遍历的非递归实现过程:
首先,从根节点A开始,根据操作1),输出A,并将其入栈,由于A的左孩子不为空,根据操作2),将B置为当前节点,再根据操作1),将B输出,并将其入栈,由于B的左孩子也不为空,根据操作2),将D置为当前节点,再根据操作1),输出D,并将其入栈,此时输出序列为ABD;
由于D的左孩子为空,根据操作3),将栈顶节点D出栈,但不输出,并将其右孩子置为当前节点;
由于D的右孩子为空,根据操作5),继续将栈顶节点B出栈,但不输出,并将其右孩子置为当前节点;
由于B的右孩子E不为空,根据操作1),输出E,并将其入栈,此时输出序列为:ABDE;
由于E的左孩子为空,根据操作3),将栈顶节点E出栈,但不输出,并将其右孩子置为当前节点;
由于E的右孩子为空,根据操作5),继续将栈顶节点A出栈,但不输出,并将其右孩子置为当前节点;
由于A的右孩子C不为空,根据操作1),输出C,并将其入栈,此时输出序列为:ABDEC;
由于A的左孩子F不为空,根据操作2),则将F置为当前节点,再根据操作1),输出F,并将其入栈,此时输出序列为:ABDECF;
由于F的左孩子为空,根据操作3),将栈顶节点F出栈,但不输出,并将其右孩子置为当前节点;
由于F的右孩子为空,根据操作5),继续将栈顶元素C出栈,但不输出,并将其右孩子置为当前节点;
此时栈空,且C的右孩子为NULL,因此遍历结束。
代码如下:
Status NRPreorder(BiTree T){
BiTree stack[MAXSIZE],pCur=T;
int top=-1;
/*pCur不为空或栈不为空时循环*/
while(pCur||top>-1){
Visit(pCur->data);/*打印当前节点*/
top++;
stack[top]=pCur;/*当前节点进栈*/
pCur=pCur->Lchild;/*在左子树上移动*/
/*若左子树为空,则让栈顶元素出栈,并在右子树上寻找直到pCur不为空*/
while(!pCur&&top>-1){
pCur=stack[top];
top--;
pCur=pCur->Rchild;
}
}
return OK;
}
二.非递归实现中序遍历
根据中序遍历的定义,先访问左子树,再访问根节点,最后访问右子树。那么依然可以借助栈实现遍历。首先声明指针pCur指向当前节点,若当前节点有左子树,则当前节点入栈,若无左子树,则打印当前节点,pCur指针进入右子树,若无右子树,则栈顶元素出栈,直到栈顶元素有右子树为止。
对于任一节点P,
1)若P的左孩子不为空,则将P入栈并将P的左孩子置为当前节点,然后再对当前节点进行相同的处理;
2)若P的左孩子为空,则输出P节点,而后将P的右孩子置为当前节点,看其是否为空;
3)若不为空,则重复1)和2)的操作;
4)若为空,则执行出栈操作,输出栈顶节点,并将出栈的节点的右孩子置为当前节点,看起是否为空,重复3)和4)的操作;
5)直到当前节点P为NULL并且栈为空,则遍历结束。
下面以上图为例详细分析其中序遍历的非递归实现过程:
首先,从根节点A开始,A的左孩子不为空,根据操作1)将A入栈,接着将B置为当前节点,B的左孩子也不为空,根据操作1),将B也入栈,接着将D置为当前节点,由于D的左子树为空,根据操作2),输出D;
由于D的右孩子也为空,根据操作4),执行出栈操作,将栈顶结点B出栈,并将B置为当前节点,此时输出序列为DB;
由于B的右孩子不为空,根据操作3),将其右孩子E置为当前节点,由于E的左孩子为空,根据操作1),输出E,此时输出序列为DBE;
由于E的右孩子为空,根据操作4),执行出栈操作,将栈顶节点A出栈,并将节点A置为当前节点,此时输出序列为DBEA;
此时栈为空,但当前节点A的右孩子并不为NULL,继续执行,由于A的右孩子不为空,根据操作3),将其右孩子C置为当前节点,由于C的左孩子不为空,根据操作1),将C入栈,将其左孩子F置为当前节点,由于F的左孩子为空,根据操作2),输出F,此时输出序列为:DBEAF;
由于F的右孩子也为空,根据操作4),执行出栈操作,将栈顶元素C出栈,并将其置为当前节点,此时的输出序列为:DBEAFC;
由于C的右孩子为NULL,且此时栈空,根据操作5),遍历结束。
代码如下:
Status NRInorder(BiTree T){
BiTree stack[MAXSIZE],pCur=T;
int top=-1;
while(pCur||top>-1){
if(pCur->Lchild){
/*如果当前节点有左子树,则入栈*/
top++;
stack[top]=pCur;
pCur=pCur->Lchild;
}
else{
Visit(pCur->data);/*无左子树,直接访问当前节点*/
pCur=pCur->Rchild;/*进入右子树继续访问*/
/*无右子树,则栈顶元素出栈并打印*/
while(!pCur&&top>-1){
pCur=stack[top];
top--;
Visit(pCur->data);
pCur=pCur->Rchild;
}
}
}
}
三.后序遍历的非递归实现
根据后续遍历的定义,先访问其左子树,再访问其右子树,最后访问其根节点,依然借助栈实现,声明两个指针pre,pCur。pCur用于指向当前节点,pre用于指向访问过的节点。
先让根节点入栈,当栈不空时,pCur指向栈顶,如果栈顶元素无左右子树或左右子树已经被输出过,则直接打印当前节点,同时栈顶元素出栈,令pre=pCur。如果不是上述情况,则令当前节点的右子树,左子树依次入栈即可。
根据后序遍历的顺序,先访问左子树,再访问右子树,后访问根节点,而对于每个子树来说,又按照同样的访问顺序进行遍历,上图的后序遍历顺序为:DEBFCA。后序遍历的非递归的实现相对来说要难一些,要保证根节点在左子树和右子树被访问后才能访问,思路如下:
对于任一节点P,
1)先将节点P入栈;
2)若P不存在左孩子和右孩子,或者P存在左孩子或右孩子,但左右孩子已经被输出,则可以直接输出节点P,并将其出栈,将出栈节点P标记为上一个输出的节点,再将此时的栈顶结点设为当前节点;
3)若不满足2)中的条件,则将P的右孩子和左孩子依次入栈,当前节点重新置为栈顶结点,之后重复操作2);
4)直到栈空,遍历结束。
下面以上图为例详细分析其后序遍历的非递归实现过程:
首先,设置两个指针:Cur指针指向当前访问的节点,它一直指向栈顶节点,每次出栈一个节点后,将其重新置为栈顶结点,Pre节点指向上一个访问的节点;
Cur首先指向根节点A,Pre先设为NULL,由于A存在左孩子和右孩子,根据操作3),先将右孩子C入栈,再将左孩子B入栈,Cur改为指向栈顶结点B;
由于B的也有左孩子和右孩子,根据操作3),将E、D依次入栈,Cur改为指向栈顶结点D;
由于D没有左孩子,也没有右孩子,根据操作2),直接输出D,并将其出栈,将Pre指向D,Cur指向栈顶结点E,此时输出序列为:D;
由于E也没有左右孩子,根据操作2),输出E,并将其出栈,将Pre指向E,Cur指向栈顶结点B,此时输出序列为:DE;
由于B的左右孩子已经被输出,即满足条件Pre==Cur->lchild或Pre==Cur->rchild,根据操作2),输出B,并将其出栈,将Pre指向B,Cur指向栈顶结点C,此时输出序列为:DEB;
由于C有左孩子,根据操作3),将其入栈,Cur指向栈顶节点F;
由于F没有左右孩子,根据操作2),输出F,并将其出栈,将Pre指向F,Cur指向栈顶结点C,此时输出序列为:DEBF;
由于C的左孩子已经被输出,即满足Pre==Cur->lchild,根据操作2),输出C,并将其出栈,将Pre指向C,Cur指向栈顶结点A,此时输出序列为:DEBFC;
由于A的左右孩子已经被输出,根据操作2),输出A,并将其出栈,此时输出序列为:DEBFCA;
此时栈空,遍历结束。
代码如下:
Status NRPostorder(BiTree T){
BiTree stack[MAXSIZE],pCur=T,pre=NULL;/*pre用于标记已访问过的节点*/
int top=-1;
stack[++top]=T;
while(top>-1){/*栈不空时循环*/
pCur=stack[top];/*pCur始终指向栈顶*/
/*如果当前节点没有左右子树或者左右子树已经被访问过*/
if((!pCur->Lchild&&!pCur->Rchild)||(pre&&(pre==pCur->Lchild||pre==pCur->Rchild))){
Visit(pCur->data);/*输出当前节点的值*/
top--;/*当前节点出栈*/
pre=pCur;/*标记为已访问过的节点*/
}
/*不是上述情况,则当前节点左右子树分别进栈*/
else{
if(pCur->Lchild)
stack[++top]=pCur;
if(pCur->Rchild)
stack[++top]=pCur;
}
}
}
四.二叉树的层序遍历
由于二叉树具有层次结构,可以按照层序进行遍历,考虑顺序问题,我们采用队列实现。从上到下从左到右依次入队。算法思路大致是先让根节点入队,若根节点有左右子树,则让左右子树依次入队,之后让队首元素出队并打印。反复进行直到队列空为止
先将树的根节点入队,
如果队列不空,则进入循环
{
将队首元素出队,并输出它;
如果该队首元素有左孩子,则将其左孩子入队;
如果该队首元素有右孩子,则将其右孩子入队
代码如下:
Status LevelOrderTraverse(BiTree T){
BiTree Queue[MAXSIZE],pCur=T;
int front=-1,tail=-1;
tail++;
Queue[tail]=pCur;/*根节点入队*/
while(front!=tail){
front++;
Visit(Queue[front]->data);/*打印队首节点*/
if(Queue[front]->Lchild){
tail++;
Queue[tail]=Queue[front]->Lchild;/*有左子树则左子树入队*/
}
if(Queue[front]->Rchild){
tail++;
Queue[tail]=Queue[front]->Rchild;
}
}
printf("\n");
}
写下这篇博文的过程中,参考了这两篇博客:
http://blog.csdn.net/ns_code/article/details/13169703
http://blog.csdn.net/ns_code/article/details/12977901
向作者表示感谢






















 1026
1026

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








