文章目录
一.序列求和的方法
1.序列求和公式
-
公式
a.等差数列: ∑ k = 1 n a k = n ( a 1 + a n ) 2 \sum_{k=1}^{n}a_k = \frac{n(a_1+a_n)}{2} ∑k=1nak=2n(a1+an)
b.等比数列:
有限项: ∑ k = 0 n a q k = a ( 1 − q n + 1 ) 1 − q \sum_{k=0}^{n}aq^k = \frac{a(1-q^{n+1})}{1-q} ∑k=0naqk=1−qa(1−qn+1);
无限项: ∑ k = 0 ∞ a q k = a 1 − q ( q < 1 ) \sum_{k=0}^\infty aq^k = \frac{a}{1-q}(q<1) ∑k=0∞aqk=1−qa(q<1)
c.调和级数: ∑ k = 1 n 1 k = ln n + O ( 1 ) \sum_{k=1}^{n}\frac1k = \ln n+O(1) ∑k=1nk1=lnn+O(1)
-
e . g . e.g. e.g.
求 ∑ t = 1 k t 2 t − 1 \sum_{t=1}^{k}t2^{t-1} ∑t=1kt2t−1
∑ t = 1 k t 2 t − 1 = ∑ t = 1 k t ( 2 t − 2 t − 1 ) − 拆项 = ∑ t = 1 k t 2 t − ∑ t = 1 k t 2 t − 1 = ∑ t = 1 k t 2 t − ∑ t = 0 k − 1 ( t + 1 ) 2 t − 变限 = ∑ t = 1 k t 2 t − ∑ t = 0 k − 1 t 2 t − ∑ t = 0 k − 1 2 t = k 2 k − ( 2 k − 1 ) = ( k − 1 ) 2 k + 1 \begin{align} &\sum_{t=1}^{k}t2^{t-1}\notag =\sum_{t=1}^{k}t(2^t-2^{t-1})-拆项\\\notag &=\sum_{t=1}^{k}t2^t-\sum_{t=1}^{k}t2^{t-1}\\\notag &=\sum_{t=1}^{k}t2^t-\sum_{t=0}^{k-1}(t+1)2^t-变限\\\notag &=\sum_{t=1}^{k}t2^t-\sum_{t=0}^{k-1}t2^t-\sum_{t=0}^{k-1}2^t\\\notag &=k2^k-(2^k-1)\\\notag &=(k-1)2^k+1 \end{align} t=1∑kt2t−1=t=1∑kt(2t−2t−1)−拆项=t=1∑kt2t−t=1∑kt2t−1=t=1∑kt2t−t=0∑k−1(t+1)2t−变限=t=1∑kt2t−t=0∑k−1t2t−t=0∑k−12t=k2k−(2k−1)=(k−1)2k+1
-
计算二分检索算法的平均时间复杂度
算法: BinarySearch(T,l,r,x)
输入:数组T,下标从l到r,数x
输出:j
伪代码:
while l<=r do m <- ceil((l+r)/2) if T[m]=x then return m else if T[m]>x then r<-m-1 else l<-m+1 return 0;设 n = 2 k − 1 n = 2^k-1 n=2k−1,n为数组长度,传入参数l = 1,r = n,x有2n+1种。其中x=T[1]…T[n]有n种,x<T[1],T[1]<x<T[2]…,x>T[n]有n+1种。设各种输入概率相同,以比较为基本运算,求平均时间复杂度
首先考虑在数组中的元素。落在正中只需比较1次,有一个元素满足;落在 1 4 \frac14 41处需比较2次,有二个元素满足;落在 1 8 \frac18 81处需要比较3次,有八个元素满足…注意到 n = 2 k − 1 = ∑ i = 0 k − 1 2 k n=2^k-1 = \sum_{i=0}^{k-1}2^k n=2k−1=∑i=0k−12k,因此最多查找k次就可以遍历到数组中的所有元素。因此需要比较的总次数为 ∑ i = 0 k − 1 ( k + 1 ) 2 k \sum_{i=0}^{k-1}(k+1)2^k ∑i=0k−1(k+1)2k,其中k+1为比较次数, 2 k 2^k 2k为满足的元素个数。
然后考虑不在数组中的元素,所有不在数组中的元素都需要比较k次才能找出来;因此比较的总次数为(n+1)*k。
因此比较的总次数为
∑ i = 0 k − 1 ( k + 1 ) 2 k + ( n + 1 ) k = ∑ i = 1 k k 2 k − 1 + ( n + 1 ) k = ( k − 1 ) 2 k + 1 + ( n + 1 ) ∗ k = ( k − 1 ) 2 k + k ∗ 2 k + 1 = ( 2 k − 1 ) 2 k + 1 \begin{align} &\sum_{i=0}^{k-1}(k+1)2^k+(n+1)k \notag \\\notag &=\sum_{i=1}^{k}k2^{k-1}+(n+1)k \\\notag &= (k-1)2^k+1+(n+1)*k \\\notag &= (k-1)2^k+k*2^k+1\notag \\ &=(2k-1)2^k+1\notag \end{align} i=0∑k−1(k+1)2k+(n+1)k=i=1∑kk2k−1+(n+1)k=(k−1)2k+1+(n+1)∗k=(k−1)2k+k∗2k+1=(2k−1)2k+1因为元素在各个位置的概率相等,因此
A ( n ) = 1 2 n + 1 ( ( 2 k − 1 ) 2 k + 1 ) = 1 2 ∗ 2 k − 1 ( ( 2 k − 1 ) 2 k + 1 ) = f ( k ) ≈ O ( log n ) \begin{align} &A(n) = \frac1{2n+1}((2k-1)2^k+1) \notag \\&= \frac1{2*2^k-1}((2k-1)2^k+1)\notag \\&= f(k)\notag \\\notag &\approx O(\log n) \end{align} A(n)=2n+11((2k−1)2k+1)=2∗2k−11((2k−1)2k+1)=f(k)≈O(logn)
2.放大法
-
两种放大法的公式
1. ∑ k = 1 n a k ≤ n a m a x 2. 若数列 a 满足 a k + 1 a k ≤ r ,则 ∑ k = 0 n a k < ∑ k = 0 ∞ a k < a 0 1 − r 1.\sum _{k=1}^{n}a_k\le na_{max}\\ 2.若数列a满足\frac{a_{k+1}}{a_k}\le r,则\sum_{k=0}^{n}a_k<\sum_{k=0}^{\infty}a_k <\frac{a_0}{1-r} 1.k=1∑nak≤namax2.若数列a满足akak+1≤r,则k=0∑nak<k=0∑∞ak<1−ra0 -
e . g . e.g. e.g.
估计 ∑ k = 1 n k 3 k \sum_{k=1}^{n}\frac{k}{3^k} ∑k=1n3kk的上界
k + 1 3 k + 1 ∗ 3 k k = 1 3 ( 1 + 1 k ) ≤ 2 3 ∑ k = 1 n k 3 k < 1 3 ∗ 1 1 − 2 3 = 1 \frac{k+1}{3^{k+1}}*\frac{3^k}{k} = \frac13(1+\frac1k)\le\frac23\\ \sum_{k=1}^{n}\frac{k}{3^k}<\frac13*\frac{1}{1-\frac23} = 1 3k+1k+1∗k3k=31(1+k1)≤32k=1∑n3kk<31∗1−321=1
二.递推方程与算法分析
1.递推方程
设序列为 a 0 , a 1 , … , a n , … a_0,a_1,\dots,a_n,\dots a0,a1,…,an,…,简记为 a n {a_n} an,一个把 a n a_n an与某些 a i ( i ∈ [ 0 , n − 1 ] ) a_i(i\in[0,n-1]) ai(i∈[0,n−1])联系起来的等式叫做关于序列 a n {a_n} an的递推方程。
-
e . g . e.g. e.g.
Fibonacci数 递推方程: f n = f n − 1 + f n − 2 f_n = f_{n-1}+f_{n-2} fn=fn−1+fn−2;初值: f 0 = 1 , f 1 = 1 f_0=1,f_1=1 f0=1,f1=1
解: f n = 1 5 ( 1 + 5 2 ) n + 1 − 1 5 ( 1 − 5 2 ) n + 1 f_n = \frac1{\sqrt 5}(\frac{1+\sqrt 5}2)^{n+1}-\frac1{\sqrt 5}(\frac{1-\sqrt 5}2)^{n+1} fn=51(21+5)n+1−51(21−5)n+1
2.递推方程与算法复杂度的关系
-
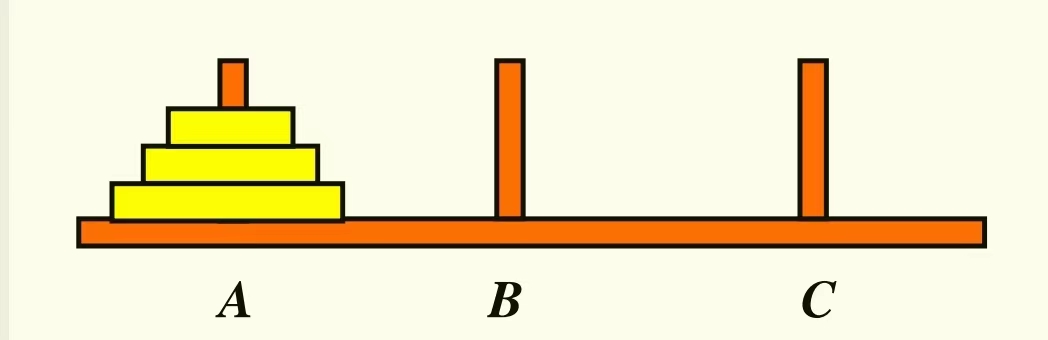
汉诺塔问题
n个盘子从大到小顺序放在A柱上,要把它们从A移动到C,每次移动1个盘子,移动时不允许大盘压在小盘上,设计一种移动方法
思路:将n-1个盘子从A移动到B,将最大的盘子移动到C,最后将n-1个盘子从B移动到C。
伪代码为
Hanoi(A,C,n)//从A移动到C,n个盘子 if n = 1 then move from A to C else Hanoi(A,B,n-1) move from A to C Hanoi(B,c,n-1)以一个盘子移动一次为基本操作,则n个盘子的移动次数为
T ( n ) = 2 T ( n − 1 ) + 1 ; 其中 T ( 1 ) = 1 解得 T ( n ) = 2 n − 1 T(n) = 2T(n-1)+1;其中T(1)=1\\ 解得T(n) = 2^n-1 T(n)=2T(n−1)+1;其中T(1)=1解得T(n)=2n−1 -
插入排序
算法:InsertSort(A,n)
输入:数组A,数组大小n
输出:排好序的数组A
伪代码:
for j<-2 to n do x<-A[j] i<-j-1 //把A[j]插入 while i>0 and x<A[i] do A[i+1]<-A[i] i<-i-1 A[i+1]<-x以一次比较为基本运算,求算法的最差时间复杂度
思路:可以从递归的角度来分析,对于n个元素的数组来说,排列n个元素等于先排列好前面n-1个元素,再排列最后的元素。在最坏情况下,最后的元素需要比较n-1次。因此我们得到了递推方程为 W ( n ) = W ( n − 1 ) + n − 1 W(n) = W(n-1)+n-1 W(n)=W(n−1)+n−1。解得 W ( n ) = n ( n − 1 ) 2 = O ( n 2 ) W(n) = \frac{n(n-1)}{2} = O(n^2) W(n)=2n(n−1)=O(n2)
三.迭代法求解递推方程
不断用递推方程的右部替换左部;
每次替换,随着n的降低在和式中多处一项;
直到出现初值停止迭代;
将初值带入并对和式求和;
可以用数学归纳法来验证解的正确性
1.直接迭代
-
汉诺塔算法
T(n) = 2T(n-1)+1;T(1) = 1
T ( n ) = 2 T ( n − 1 ) + 1 = 2 [ 2 T ( n − 2 ) + 1 ] + 1 = 2 2 T ( n − 2 ) + 2 + 1 … = 2 n − 1 T ( 1 ) + 2 n − 2 + 2 n − 3 + ⋯ + 1 = 2 n − 1 + ( 2 n − 1 − 1 ) = 2 n − 1 \begin{align}\notag &T(n) = 2T(n-1)+1\\\notag &=2[2T(n-2)+1]+1\\\notag &=2^2T(n-2)+2+1\\\notag &\dots\\\notag &=2^{n-1}T(1)+2^{n-2}+2^{n-3}+\dots+1\\\notag &=2^{n-1} +(2^{n-1}-1)\\\notag &=2^n-1 \end{align} T(n)=2T(n−1)+1=2[2T(n−2)+1]+1=22T(n−2)+2+1…=2n−1T(1)+2n−2+2n−3+⋯+1=2n−1+(2n−1−1)=2n−1
-
插入排序算法
W(n) = W(n-1)+n-1;W(n) = 0
W ( n ) = W ( n − 1 ) + n − 1 = W ( n − 2 ) + n − 2 + n − 1 … = W ( 1 ) + 1 + ⋯ + n − 1 = ( n − 1 ) n 2 \begin{align}\notag &W(n) = W(n-1)+n-1\\\notag &=W(n-2)+n-2+n-1\\\notag &\dots\\\notag &=W(1)+1+\dots+n-1\\\notag &=\frac{(n-1)n}{2}\notag \end{align} W(n)=W(n−1)+n−1=W(n−2)+n−2+n−1…=W(1)+1+⋯+n−1=2(n−1)n
2.换元迭代
-
二分归并排序
算法:MergeSort(A,p,r)
输入:数组A[p…r]
输出:按照递增顺序排列的数组
伪代码
if p<r then q<-ceil((p+r)/2) MergeSort(A,p,q) MergeSort(A,q+1,r) Merge(A,p,q,r)递推公式为W(n) = 2W(n/2)+n-1,W(1) = 0,求W(n),其中 n = 2 k n=2^k n=2k
将n换元为n=2^k,方程变为 W ( 2 k ) = 2 W ( 2 k − 1 ) + n − 1 W(2^k) = 2W(2^{k-1})+n-1 W(2k)=2W(2k−1)+n−1
W ( 2 k ) = 2 W ( 2 k − 1 ) + n − 1 = 2 [ 2 W ( 2 k − 2 + 2 k − 1 − 1 ) ] + 2 k − 1 = … = 2 k W ( 1 ) + k 2 k − ( 2 k − 1 + 2 k − 2 + ⋯ + 2 + 1 ) = k 2 k − 2 k + 1 = n log n − n + 1 \begin{align}\notag &W(2^k) = 2W(2^{k-1})+n-1\\&=\notag 2[2W(2^{k-2}+2^{k-1}-1)]+2^k-1\\&\notag =\dots\\&=\notag 2^kW(1)+k2^k-(2^{k-1}+2^{k-2}+\dots+2+1)\\&=\notag k2^k-2^k+1\\&=\notag n\log n -n+1 \end{align} W(2k)=2W(2k−1)+n−1=2[2W(2k−2+2k−1−1)]+2k−1=…=2kW(1)+k2k−(2k−1+2k−2+⋯+2+1)=k2k−2k+1=nlogn−n+1
3.使用数学归纳法进行验证
-
e . g . e.g. e.g.
证明:递推方程的解为W(n) = n(n-1)/2;递推方程为:W(n) = W(n-1)+n-1;W(1) = 0
使用数学归纳法证明: W ( 1 ) = 0 设对于 n , 解满足方程 W ( n + 1 ) = W ( n ) + n = n ( n − 1 ) 2 + n = n ( n + 1 ) 2 使用数学归纳法证明:\\ W(1) = 0\\ 设对于n,解满足方程\\ W(n+1) = W(n)+n = \frac{n(n-1)}{2}+n=\frac{n(n+1)}{2} 使用数学归纳法证明:W(1)=0设对于n,解满足方程W(n+1)=W(n)+n=2n(n−1)+n=2n(n+1)
四.差消法化简高阶递推方程
-
快速排序
设A[p…r]的元素彼此不等,以首元素A[1]对数组进行划分,使得:
小于x的元素放在A[p…q-1];大于x的元素放在A[q+1…r]
递归对A[p…q-1]和A[q+1…r]进行排序,则
工作量 = 子问题的工作量 + 划分工作量
有n种可能的输入
x排好序的位置 子问题1的规模 子问题2的规模 1 0 n-1 2 1 n-2 … … … n n-1 0 其中对于每个输入,划分所需要的比较次数都为n-1(需要遍历比较数组中的其他元素)
求快速排序的平均工作量T(n)
首先计算总工作量,用总工作量除以n即可得到A(n)。
T ( 0 ) + T ( n − 1 ) + n − 1 T ( 1 ) + T ( n − 2 ) + n − 1 … T ( n − 1 ) + T ( 0 ) + n − 1 \begin{align}\notag &T(0) +T(n-1)+n-1\\&\notag T(1) + T(n-2)+n-1\\&\notag \dots\\&\notag T(n-1)+T(0)+n-1 \end{align} T(0)+T(n−1)+n−1T(1)+T(n−2)+n−1…T(n−1)+T(0)+n−1
上面的n个式子累加得到
2 ∑ i = 0 n − 1 T ( i ) + n ( n − 1 ) 2\sum_{i=0}^{n-1}T(i)+n(n-1) 2i=0∑n−1T(i)+n(n−1)
因此平均工作量的递推表达式为
T ( n ) = 1 n [ 2 ∑ i = 0 n − 1 T ( i ) + n ( n − 1 ) ] = 1 n ( 2 ∑ i = 0 n − 1 T ( i ) + c n ) \begin{align}\notag &T(n) =\frac1n[2\sum_{i=0}^{n-1}T(i)+n(n-1)]\\& = \frac1n(2\sum_{i=0}^{n-1}T(i)+cn)\notag \end{align} T(n)=n1[2i=0∑n−1T(i)+n(n−1)]=n1(2i=0∑n−1T(i)+cn)计算上面的式子需要用到差消化简的技巧
T ( n ) = 1 n ( 2 ∑ i = 0 n − 1 T ( i ) + c n ) T ( n − 1 ) = 1 n − 1 [ 2 ∑ i = 0 n − 2 T ( i ) + c ( n − 1 ) ] n T ( n ) − ( n − 1 ) T ( n − 1 ) = 2 ∑ i = 0 n − 1 T ( i ) + c n 2 − 2 ∑ i = 0 n − 2 T ( i ) + c ( n − 1 ) 2 = 2 T ( n − 1 ) + c 1 n T ( n ) n + 1 = T ( n − 1 ) n + c 1 n + 1 经过迭代化简得 T ( n ) = ( n + 1 ) c 1 ∑ i = 3 n + 1 1 i = Θ ( n log n ) \begin{align}\notag &T(n) = \frac1n(2\sum_{i=0}^{n-1}T(i)+cn)\\&\notag \\&\notag T(n-1) = \frac1{n-1}[2\sum_{i=0}^{n-2}T(i)+c(n-1)]\\&\notag \\&\notag nT(n)-(n-1)T(n-1)\\&=\notag 2\sum_{i=0}^{n-1}T(i)+cn^2 - 2\sum_{i=0}^{n-2}T(i)+c(n-1)^2\\&=\notag 2T(n-1) +c_1n\\&\notag \\&\notag \frac{T(n)}{n+1} = \frac{T(n-1)}{n}+\frac{c_1}{n+1}\\&\notag 经过迭代化简得 \\&T(n) = (n+1)c_1\sum_{i=3}^{n+1}\frac1i = \Theta(n\log n)\notag \end{align} T(n)=n1(2i=0∑n−1T(i)+cn)T(n−1)=n−11[2i=0∑n−2T(i)+c(n−1)]nT(n)−(n−1)T(n−1)=2i=0∑n−1T(i)+cn2−2i=0∑n−2T(i)+c(n−1)2=2T(n−1)+c1nn+1T(n)=nT(n−1)+n+1c1经过迭代化简得T(n)=(n+1)c1i=3∑n+1i1=Θ(nlogn)
五.递归树
- 递归树是迭代计算的模型
- 递归树的生成过程与迭代过程一致
- 递归树上的所有项恰好是迭代之后产生和式中的项
- 对递归树上的项求和就是迭代后方程的解
-
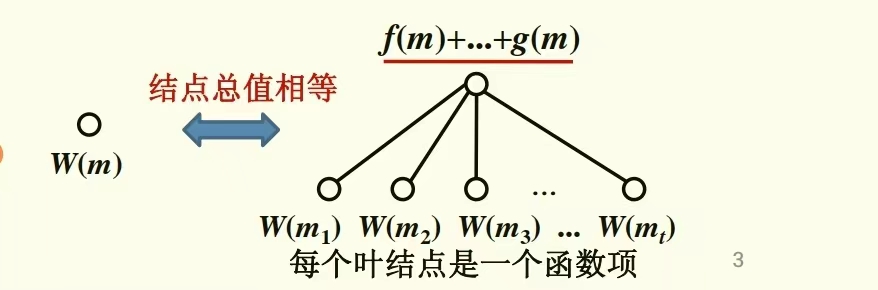
迭代在递归树中的表示
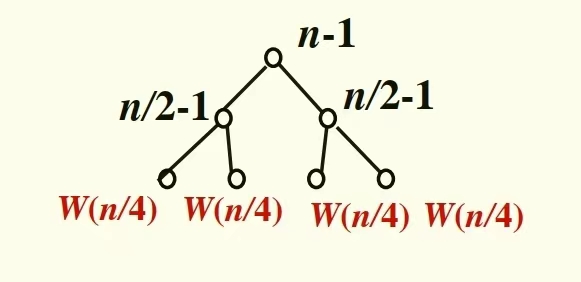
若递归树上的某节点标记为W(m),且 W ( m ) = ∑ i = 1 t W ( m i ) + f ( m ) ⋯ + g ( m ) W(m) = \sum_{i=1}^{t}W(m_i)+f(m)\dots+g(m) W(m)=∑i=1tW(mi)+f(m)⋯+g(m),则其中 W ( m i ) W(m_i) W(mi)称为函数项,W(m)可以表示如下图的形式
e . g e.g e.g
二分归并排序的递推方程为 W ( n ) = 2 W ( n 2 ) + n − 1 W( n) = 2W(\frac n2)+n-1 W(n)=2W(2n)+n−1,试画出这个递推方程所对应的递归树
-
递归树的生成
-
初始,递归树只有根节点,其值为W(n)
-
不断重复下述过程:
将函数项叶节点的迭代式W(n)表示为二层子树
用该子树替换叶节点
-
继续递归树的生成,直到书中没有函数项(只有初值)为止
e . g . e.g. e.g.
生成 W ( n ) = 2 W ( n 2 ) + n − 1 W( n) = 2W(\frac n2)+n-1 W(n)=2W(2n)+n−1的递归树
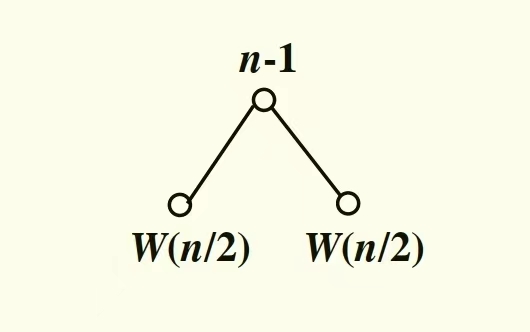
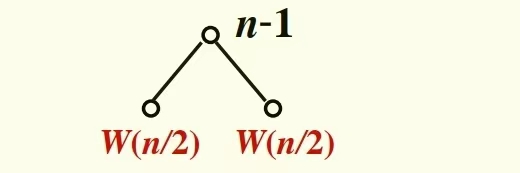
第一步 W(n)->2 W(n/2)+n-1
第二步W(n/2)->2 W(n/4)+n/2-1
…
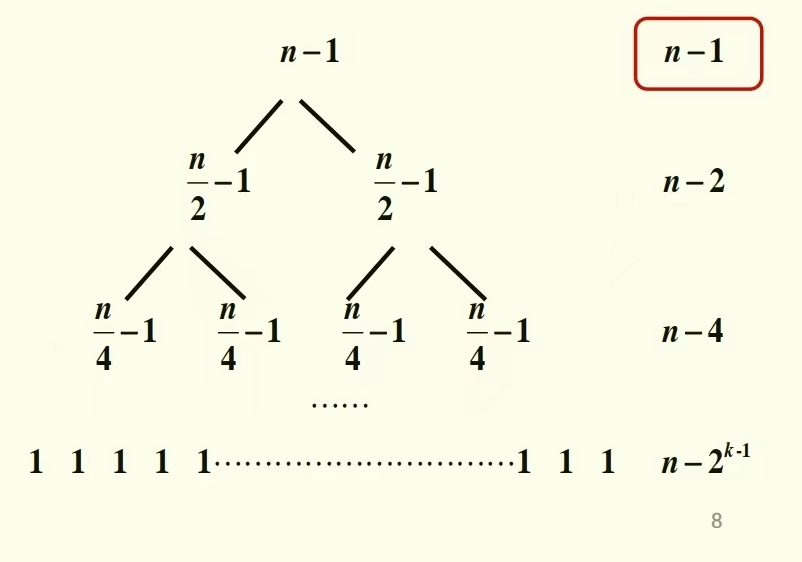
最后结果为
可以看到,递归树的第一层的和为n-1,第二层为n-2,最后一层为 n − 2 k − 1 n-2^{k-1} n−2k−1,因此可以直观的求得递推方程的通式
-
-
e . g . e.g. e.g.
利用递归树的方法求得 T ( n ) = T ( 1 3 ) + T ( 2 n 3 ) + n T(n)=T(\frac13)+T(\frac{2n}3)+n T(n)=T(31)+T(32n)+n的渐进上界
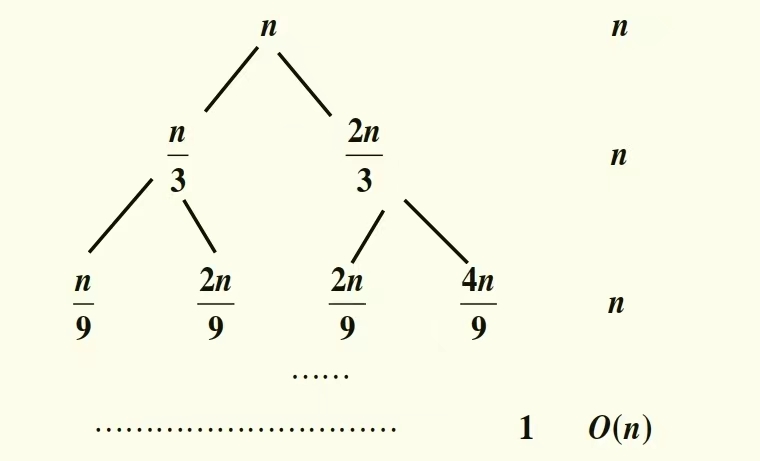
得递归树如下图所示
但是图中的递归树并不对称,左边短于右边。但由于求的是渐进上界,所以只需要按最多层数算即可。
树的层数为 log 3 2 n \log{\frac32}n log23n,因此 T ( n ) = Θ ( n log n ) T(n) = \Theta(n\log n) T(n)=Θ(nlogn)
六.主定理
1.主定理
当递推方程的形式如下时,可以使用主定理
T ( n ) = a T ( n b ) + f ( n ) T(n) = aT(\frac nb)+f(n) T(n)=aT(bn)+f(n),其中a为规约后的子问题个数, n b \frac n b bn为归约后的子问题规模,f(n)为归约过程及子问题的解的工作量
则
若 ∃ ϵ > 0 , s . t . f ( n ) = O ( n log b a − ϵ ) , 那么 T ( n ) = Θ ( n log b a ) 若\exists \epsilon >0,s.t. f(n) = O(n^{\log_ba-\epsilon}),那么T(n) = \Theta(n^{\log_ba}) 若∃ϵ>0,s.t.f(n)=O(nlogba−ϵ),那么T(n)=Θ(nlogba)
若 f ( n ) = Θ ( n log b a ) , 那么 T ( n ) = Θ ( n log b a log n ) 若f(n) = \Theta(n^{\log_ba}),那么T(n) = \Theta(n^{\log_ba}\log n) 若f(n)=Θ(nlogba),那么T(n)=Θ(nlogbalogn)
若 ∃ ϵ > 0 , s . t . f ( n ) = Ω ( n log b a + ϵ ) , 且对于某个常数 c < 1 和充分大的 n ,满足 a f ( n b ) ≤ c f ( n ) , 那么 T ( n ) = Θ ( f ( n ) ) 若\exists \epsilon >0,s.t. f(n) = \Omega(n^{\log_ba+\epsilon}),且对于某个常数c<1和充分大的n,满足af(\frac nb)\le cf(n),那么T(n) = \Theta(f(n)) 若∃ϵ>0,s.t.f(n)=Ω(nlogba+ϵ),且对于某个常数c<1和充分大的n,满足af(bn)≤cf(n),那么T(n)=Θ(f(n))
定理的三条分别代表f(n)的阶小于 n log b a n^{\log _b a} nlogba、等于 n log b a n^{\log _b a} nlogba和大于 n log b a n^{\log _b a} nlogba的情况。其中大于 n log b a n^{\log _b a} nlogba时,需要验证额外的条件
- 证明略
2.使用主定理求解递推方程
-
主定理第一条
求解递推方程 T ( n ) = 9 T ( n 3 ) + n T(n) = 9T(\frac n3) + n T(n)=9T(3n)+n
log b a = log 3 9 = 2 n = O ( n 2 ) T ( n ) = Θ ( n 2 ) \log_ba = \log_39 = 2\\ n=O(n^2)\\ T(n) = \Theta(n^2) logba=log39=2n=O(n2)T(n)=Θ(n2)
-
主定理第二条
求解递推方程 T ( n ) = T ( 2 n 3 ) + 1 T(n) =T(\frac{2n}{3})+1 T(n)=T(32n)+1
log b a = log 3 2 1 = 0 1 = Θ ( 1 ) T ( n ) = Θ ( log n ) \log_ba = \log_\frac 3 2 1 = 0\\ 1 = \Theta(1)\\ T(n) = \Theta(\log n) logba=log231=01=Θ(1)T(n)=Θ(logn)
-
主定理第三条
求解递推方程 T ( n ) = 3 T ( n 4 ) + n log n T(n) = 3T(\frac n4)+n\log n T(n)=3T(4n)+nlogn
log b a = log 4 3 < 1 n log n = Ω ( n ) 验证条件 : 3 f ( n 4 ) = 3 4 n log n 当 c ∈ [ 3 4 , 1 ) 时,有 3 f ( n 4 ) ≤ c f ( n ) T ( n ) = Θ ( n log n ) \log_ba = \log_43 <1 \\ n\log n=\Omega(n)\\ 验证条件:\\ 3f(\frac n 4) = \frac 3 4 n\log n\\ 当c\in[\frac 34 ,1)时,有3f(\frac n 4)\le cf(n)\\ T(n) = \Theta(n\log n) logba=log43<1nlogn=Ω(n)验证条件:3f(4n)=43nlogn当c∈[43,1)时,有3f(4n)≤cf(n)T(n)=Θ(nlogn)
-
不能使用主定理的例子
求解递推方程 T ( n ) = 2 T ( n 2 ) + n log n T(n) = 2T(\frac n 2)+n\log n T(n)=2T(2n)+nlogn
log b a = log 2 2 = 1 n log n = Ω ( n ) 验证条件 : a f ( n b ) = n log n 不存在这样的 c ∈ ( 0 , 1 ) , 满足 a f ( n b ) ≤ c f ( n ) 因此不能使用主定理 \log _b a =\log_22 =1\\ n\log n=\Omega(n)\\ 验证条件:\\ af(\frac n b) = n\log n\\ 不存在这样的c\in(0,1),满足af(\frac n b)\le cf(n)\\ 因此不能使用主定理\\ logba=log22=1nlogn=Ω(n)验证条件:af(bn)=nlogn不存在这样的c∈(0,1),满足af(bn)≤cf(n)因此不能使用主定理
可以使用递归树来求解。递推方程的递推树如下图
然后根据递归树求解方程
T ( n ) = ∑ i = 0 k − 1 n ( log n − i ) , 其中 k = log n 则 T ( n ) = k ( n log n ) − n [ k ( 0 + k − 1 ) 2 ] = n log 2 n − n log 2 n − log n 2 = Θ ( n l o g 2 n ) T(n) = \sum_{i=0}^{k-1}n(\log n-i) ,其中k = \log n\\ 则T(n) = k (n\log n)-n[\frac {k(0+k-1)}2]\\ =n\log ^ 2 n-n\frac{\log ^2 n-\log n}{2} = \Theta(nlog^2n) T(n)=i=0∑k−1n(logn−i),其中k=logn则T(n)=k(nlogn)−n[2k(0+k−1)]=nlog2n−n2log2n−logn=Θ(nlog2n)
七.习题
求解以下递推方程
T
(
n
)
=
T
(
n
−
1
)
+
n
2
;
其中
T
(
1
)
=
1
T(n) = T(n-1)+n^2;其中T(1) = 1
T(n)=T(n−1)+n2;其中T(1)=1
求解以下递推方程
T
(
n
)
=
9
T
(
n
3
)
+
n
;
其中
T
(
1
)
=
1
T(n) = 9T(\frac n 3)+n;其中T(1) = 1
T(n)=9T(3n)+n;其中T(1)=1
求解以下递推方程
T
(
n
)
=
T
(
n
2
)
+
T
(
n
4
)
+
c
n
;
其中
T
(
1
)
=
1
T(n) = T(\frac n2)+T(\frac n4)+cn;其中T(1) = 1
T(n)=T(2n)+T(4n)+cn;其中T(1)=1
参考答案(答案为笔者自己所做,限于水平,其中存在错误在所难免,欢迎大家指正)
思路:使用迭代法
T
(
n
)
=
T
(
n
−
1
)
+
n
2
=
T
(
n
−
2
)
+
(
n
−
1
)
2
+
n
2
=
…
=
T
(
1
)
+
∑
i
=
0
n
−
1
(
n
−
i
)
2
=
∑
i
=
1
n
i
2
\begin{align}\notag &T(n) = T(n-1)+n^2\\&=\notag T(n-2)+(n-1)^2+n^2\\&=\notag \dots\\&=\notag T(1)+\sum_{i=0}^{n-1}(n-i)^2\\&=\notag \sum_{i=1}^ni^2 \end{align}
T(n)=T(n−1)+n2=T(n−2)+(n−1)2+n2=…=T(1)+i=0∑n−1(n−i)2=i=1∑ni2
思路:使用主定理
log
b
a
=
log
3
9
=
2
n
=
O
(
n
2
)
T
(
n
)
=
Θ
(
n
2
)
\log _ba = \log _3 9 = 2\\ n = O(n^2)\\ T(n) = \Theta(n^2)
logba=log39=2n=O(n2)T(n)=Θ(n2)
思路:使用递归树
画出递归树后,第一层的和为cn,第二层的和为
3
4
c
n
\frac 3 4cn
43cn,第k层的和为
(
3
4
)
k
c
n
(\frac34)^kcn
(43)kcn,而递归树最多有
log
n
\log n
logn层,因此有
T
(
n
)
≤
∑
i
=
0
log
n
3
4
c
n
≤
∑
i
=
0
∞
3
4
c
n
=
1
1
−
3
4
c
n
=
Θ
(
n
)
T(n)\le\sum_{i=0}^{\log n}\frac 3 4 cn\le \sum_{i=0}^{\infty}\frac 3 4 cn = \frac{1}{1-\frac34}cn = \Theta(n)
T(n)≤i=0∑logn43cn≤i=0∑∞43cn=1−431cn=Θ(n)








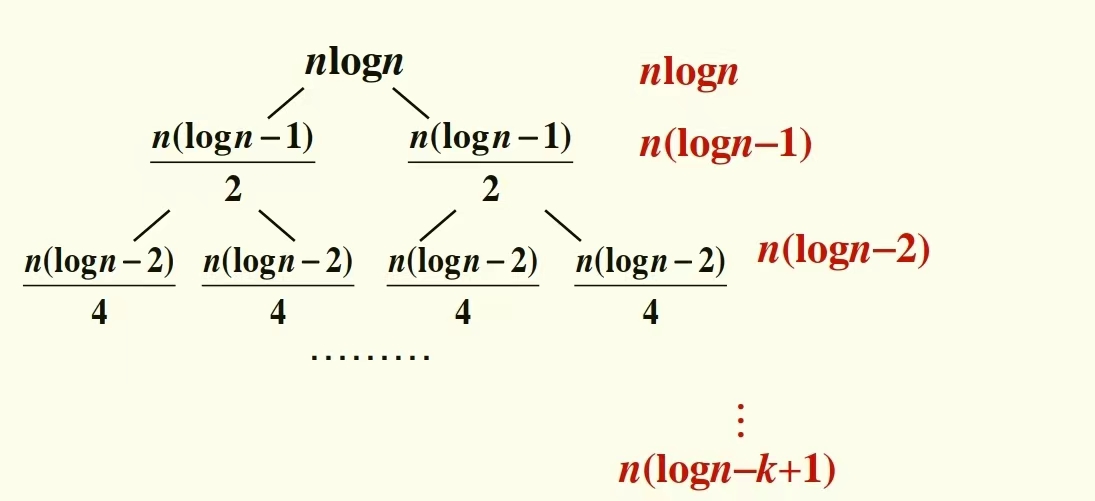

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








