WGS1984快速度确定平面坐标系UTM分带（快速套表、公式计算、软件范围判定）

于 2024-09-22 20:01:42 发布
阅读量2.3k 收藏 28
点赞数 27
分类专栏： ArcGIS实战应用技巧 文章标签： arcgis WGS1984 UTM 坐标系转换 6°带 中央经线
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/kinghxj/article/details/142442471
版权

        之前我们介绍了坐标系3°带6°带快速确定带号及中央经线（快速套表、公式计算、软件范围判定）就，讲的是CGCS2000 高斯克吕格的投影坐标系。

        那还有我们经常用的WGS1984的平面坐标系一般用什么投影呢?

对于全球全国的比如在线地图使用：WGS 1984 Web Mercator (auxiliary sphere)，也会使用Albers投影。

图片

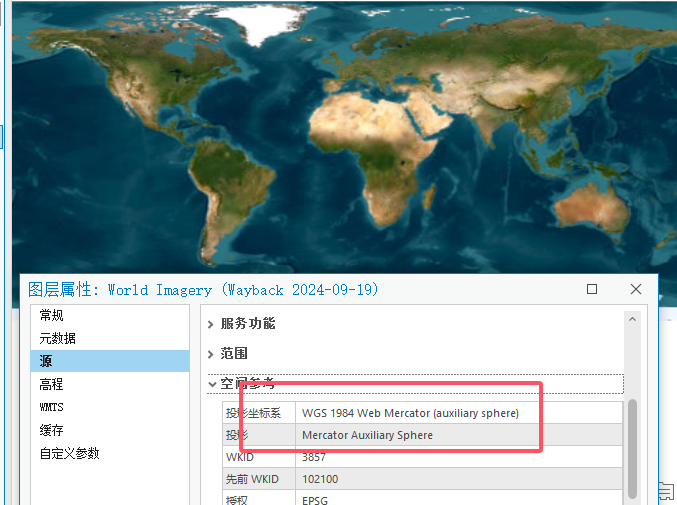
Web Mercator投影：

球面墨卡托，多用与发布的在线地图，将地球椭球体直接视为球体。

     但是我们使用最多的应该是UTM投影，我们经常下载的DEM、影像数据基本都是UTM的分带投影。现在我们对UTM进行介绍，以及如何进行UTM的快速分带选择。

图片

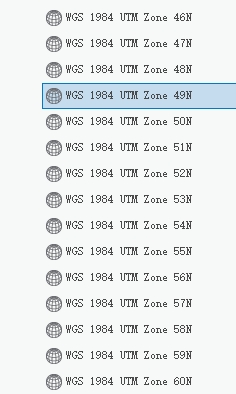
目录：1、快速套图表，2、公式计算，3、软件坐标范围选择判定。

一、 UTM投影介绍

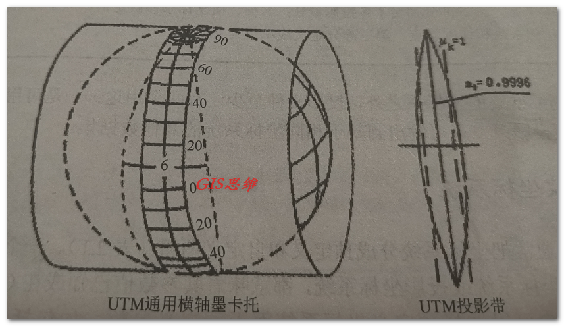
       通用横轴墨卡托投影(UTM，Universal Transverse Mercator)：横轴等角割圆柱投影，椭圆柱割地球南纬80度，北纬84度两条登高圈，投影后两条相割的经线没有变形，而中央经线上的长度比为0.9996。

        我国的卫星影像资料常采用WGS84下的UTM投影。亦是采用分带投影，分带方法与GK相似，但是由西经180°起每隔6°自西向东分带，将地球分为60个投影带，中国跨43-53带。

图片

下图可以直接确定各个经度所在的UTM坐在的带号。

图片

图片

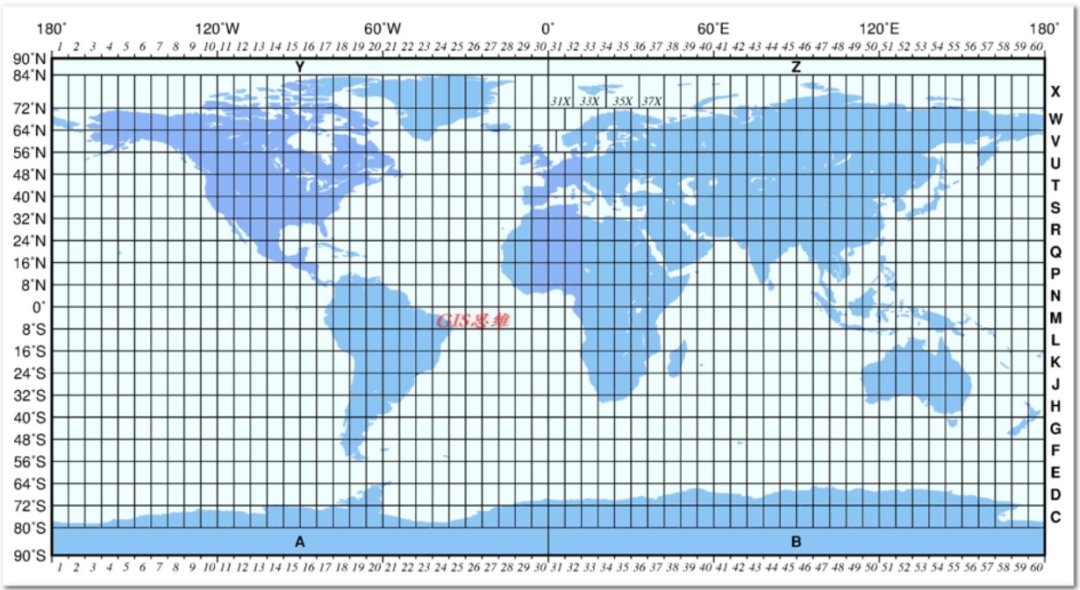
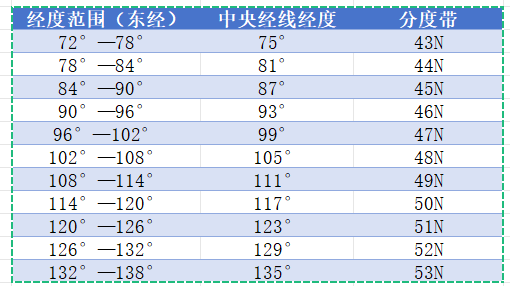
    这样够清楚了吧，不管你的数据是在哪一个区域，我随时可以查阅。

比如福建省福州市：

福州市经纬度 福州市的经纬度坐标为北纬25°15′～26°39′，东经118°08′～120°31′。这个位置使福州成为了中国东南沿海的重要城市，与台湾隔海相望，地理位置优越

百度百科

福州118°08′～120°31′经度范围一套上面图，大概就是Zone50.也有少部分在Zone51

图片

二、 公式计算

  有时候，我们一下子急的很，找不到图表，我们也是可以直接通过公式计算。已知某一地的中心点经度118.3度，可以公式计算：

带号 N =Int（(经度)/6）+31根据已知经度计算高斯克吕格投影的带号：(118.3)/3=19.71666666666667取整数+31=50

图片

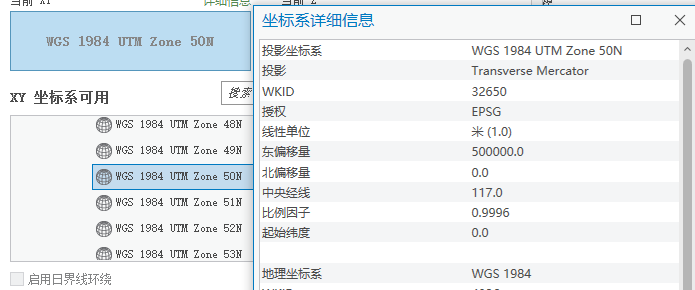
三、 根据软件坐标文件判断

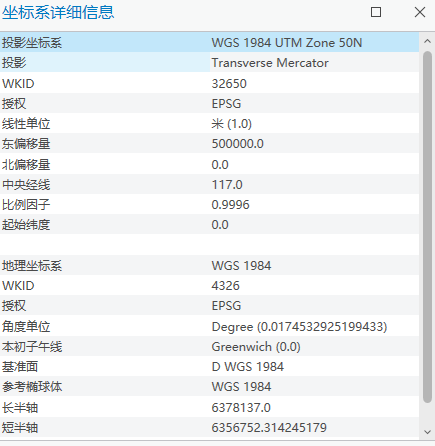
  还有时候，我们没有表也记不得公式，那怎么办? 我们在用ArcGIS的定义做坐标系的时候，会看到对应的选择是有具体信息的。

比如这个：投影坐标系WGS 1984 UTM Zone 50N

图片

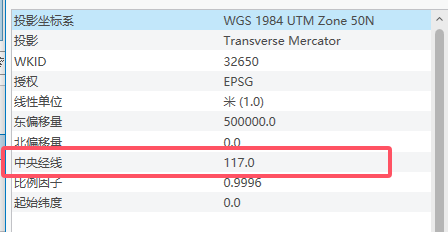
        我们还是上一份数据某一地的中心点经度118.3度，

图片

        我们很容易判断这个UTM带的的范围为117-3到117+3，即114°～120°。118.3在114°～120°在这个范围内，也就选定了WGS 1984 UTM Zone 50N。

一起来参加我们的系统学习吧

图片

▼资源与学习▼

 推荐学习

ArcGIS全系列实战视频教程——9个单一课程组合
4大遥感软件！遥感影像解译！ArcGIS+ENVI+Erdas+eCognition
ArcGIS10.X入门实战视频教程（GIS思维）
ArcGIS之模型构建器（ModelBuilder）视频教程
ArcGIS之遥感影像分类及成果应用视频课程
ArcPy结合数据驱动模块的批量制图
ArcGIS之Data Reviewer空间数据质量检查
WGS1984UTM去投影 转成WGS1984
04-30
将经过utm投影后的坐标重新去投影，即将地理坐标转经纬度，使用时只需修改一下带号即可
自动驾驶 坐标系转换 WGS84转UTM坐标系 墨卡托投影
11-24
由于将WGS84坐标系转化为UTM坐标系大多都是C或者C++代码，对于尝试用matlab的小伙伴来说，可能是对C/C++不熟悉或者不愿意自己动手去转换，所以我上传了使用matlab/simulink写的WGS84坐标系转化为UTM坐标系程序；...
快速查找WGS1984 坐标地理坐标系转UTM投影坐标的多种方法
陆杨0321的博客
07-31 5872
快速查找WGS1984 坐标地理坐标系转UTM投影坐标的多种方法
WGS84、GCJ02、BD09和CGCS2000地理坐标系详解
qq_42837317的博客
07-26 4834
在WGS84、GCJ-02、BD-09和CGCS2000坐标系之间的转换中，6度分带和3度分带的参数并不直接使用，因为这些转换主要是地理坐标系之间的转换，而不是投影坐标系之间的转换。在直接进行WGS84、GCJ-02、BD-09和CGCS2000地理坐标系之间的转换时，不涉及平面坐标系（如高斯-克吕格或UTM）的转换，因此不需要使用6度分带和3度分带的参数。BD-09（百度坐标系）是百度公司推出的一种地理坐标系统，它基于GCJ-02（火星坐标系）进行进一步的加密和偏移处理。（见文章末尾的示例）
WGS84 UTM 坐标系及UTM投影分带标准
qq_38378235的博客
08-15 3万+
1.  UTM (Universal Transverse Mercator)坐标系是由美国军方在1947提出的。虽然我们仍然将其看作与“高斯－克吕格”相似的坐标系统，但实际上UTM采用了网格的分带（或分块）。除在美国本土采用Clarke 1866椭球体以外，UTM在世界其他地方都采用WGS84。UTM是由美国制定，因此起始分带并不在本初子午线，而是在180度，因而所有美国本土都处于0－30带内。...
UTM坐标系
wenningshine的博客
11-14 1841
这个投影简单来说就是从地心发出一条射线，经地表一点，在向外，与地球的外切圆柱体（南北方向交于一点），这个交点就是地表的这个点的墨卡托投影点。UTM的好处之一是，在这个UTM地图上连接两点画一条直线，再投影回地球上，如果有一条船在这两点之间航行，那么它不需要动罗盘就可以直达。纬度分区：编号C-X(不含I,O,共20个区)，每个区的南北跨度为 8°。2、UTM坐标系在经度方向分为60个区，每个区6度，一共360度。1、UTM坐标系是投影坐标系。如何投影：墨卡托投影。
UTM 坐标系
alex1801
09-19 5474
UTM(Universal Transverse Mercator Grid System, 通用横墨卡托网格系统)
UTM坐标系转WGS84坐标系C#代码，详细
01-02
3. **计算转换参数**：这包括UTM坐标系到WGS84坐标系的转换参数，如投影中心的纬度、中央经线的经度、以及比例因子等。这些参数在UTM坐标系定义时就已经确定。 4. **应用墨卡托投影**：使用横轴墨卡托投影公式，将...
UTM坐标转换大地坐标系
04-23
UTM坐标转换大地坐标系转换，详细介绍了UTM到大地坐标系的转换方法，地理信息工作者适用
中国政区图（地理坐标系WGS-84）
12-13
中国政区图，GCS地理坐标系WGS-84 值得下载！！！
在ros中使用geodesy进行wgs坐标系转utm坐标系
12-22
`geodesy`是ROS中的一个包，专门用于处理地理坐标系统之间的转换，如从全球定位系统（WGS84）坐标系转换到统一世界坐标系统（UTM）。 WGS84是一种全球性的大地坐标系统，广泛用于GPS定位，其中经纬度是其主要表示...
GIS点、线、面数据WGS1984转百度坐标系、火星坐标系
02-28
转换过程中需要考虑坐标系的投影方式，WGS1984通常采用经纬度表示，而百度和火星坐标系则常用于平面直角坐标表示。 5. **应用场景**：坐标系转换在地图开发、定位服务、数据分析等领域有广泛应用。例如，如果你有一...
什么是UTM坐标系
12-27 5530
1.概述 UTM（Universal Transverse Mercator Grid System，通用横墨卡托格网系统）坐标是一种平面直角坐标，这种坐标格网系统及其所依据的投影已经广泛用于地形图，作为卫星影像和自然资源数据库的参考格网以及要求精确定位的其他应用。 2.UTM投影背景 UTM投影为美国陆军工程兵测绘局（Army Map Service，US Army Corps of ...
WGS1984 -UTM投影问题
水滴石穿，绳锯木断
03-21 2万+
关于WGS1984投影坐标系的相关知识： 打开WGS1984投影文件，仔细看看，我们可以发现里面中有三种不同的投影文件：如下： WGS1984 BLM Zone 14N(ftvs).prj WGS 1984 Complex UTM Zone 20N.prj (该处由20N——30N) WGS 1984 UTM Zone 9s.prj(该处由9s——60s)此处的S代表南半球，同样北半球有同
WGS84与WGS84 Web Mercator
weixin_34245169的博客
11-25 2187
1. WGS84与WGS84 Web Mercator 1.1 关于WGS1984投影坐标系 UTM (Universal Transverse Mercator)坐标系是由美国军方在1947提出的。虽然我们仍然将其看作与“高斯－克吕格”相似的坐标系统，但实际上UTM采用了网格的分带（或分块）。除在美国本土采用Clarke 1866椭球体以外，UTM在世界其他地方都采用WGS84。 UT...
WGS 1984地理坐标系的墨卡托投影分度带（UTM ZONE）选择方法
热门推荐
aganliang的专栏
10-12 13万+
如果要在ArcMAP中启用shape.area和shape.length计算（几何计算），需要设置投影坐标，WGS-1984地理坐标系一般都设置为UTM投影，涉及不同经纬度不同分带选择，下面详细介绍一下UTM投影。 UTM 投影(Universal Transverse Mercator，通用横轴墨卡托投影)是由美国军方在1947提出的，美国本土采用Clarke ...
UTM坐标系区号选择
yumosihen的博客
10-30 8138
UTM坐标系区号选择与说明
wgs84 坐标系转换utm坐标系计算公式
最新发布
12-27
### WGS84到UTM坐标的转换 WGS84坐标系是一个全球定位系统的标准地理坐标体系，而通用横轴墨卡托投影(UTM)是一种用于表示地球表面位置的地图投影方法。两者之间的转换涉及到一系列复杂的数学运算。 #### 转换过程概述 为了实现从WGS84到UTM的转换，通常会遵循以下公式： 1. **定义常量** 需要先设定一些椭球体参数以及其它必要的数值： - \( a \): 半径 (对于WGS84, 这个值大约为6378137米)[^1] - \( f \): 扁率 (约为1 / 298.257223563) 2. **计算中间变量** 使用给定的经纬度(\( lat \),\( lon \))来求解几个重要的辅助量: ```python e = math.sqrt((2 * f) - pow(f, 2)) N = a / math.sqrt(1 - pow(e * math.sin(math.radians(lat)), 2)) ``` 3. **确定带号和中心子午线** UTM分为多个区域，每个区域内都有特定的中央经线。可以根据输入的经度找到对应的UTM区并获取其中心子午线的位置。 ```python zone_number = int((lon + 180) / 6) + 1 if zone_number == 0: zone_number = 1 central_meridian = (zone_number - 1) * 6 - 180 + 3 ``` 4. **应用具体的变换方程** 接下来利用上述准备好的数据完成最终的空间坐标映射： ```python n = a / math.sqrt(1 - pow(e, 2)) A = e / 2 + ((e**3)/8) + (((e**5)*5)/16) B = ((e**2)/4) + ((e**4)*5/16) C = (3*(e**3))/8 + (5*(e**5)*3)/16 D = (15*(e**4))/256 + (45*(e**6))/1024 E = (35*(e**5))/256 phi_prime = lat * math.pi / 180 lambda_prime = (lon - central_meridian) * math.pi / 180 v = n / math.sqrt(1 - (pow(e*math.sin(phi_prime), 2))) p = v * math.cos(phi_prime) T = pow(tan(phi_prime), 2) C_ = (pow(e, 2)*(pow(cos(phi_prime), 2))) / (1-e*e) A_ = (lambda_prime*p)/(factorial(2)) J2 = (p*(-1-2*T+C_))/(factorial(4))*pow(lambda_prime, 3) J4 = (p*(5+28*T+24*pow(T, 2)+ \ (-6-8*T)*C_+(4*C_*C_)-24*T*C_))\ /(factorial(6))*pow(lambda_prime, 5) J6 = (p*(-61-662*T+1320*pow(T, 2)\ -(720*power(T, 3))+(-479*C_)+(1792*T*C_)\ +(308*C_*C_)-(192*T*C_*C_)))\ /(factorial(8))*pow(lambda_prime, 7) easting = K0 * (A_ + J2 + J4 + J6) + 500000 northing = K0 * (v*tan(phi_prime)*(1+T/3-(T*T)/15-T*C_/9+ \ (4+T)*C_/(360))- \ (tan(phi_prime)/3)*(J2+J4+J6)+ \ tan(phi_prime)/45*(4*pow(J2, 2)+ \ 3*J4- \ pow(J2, 2)*J2-J6)) + NorthingOffset ``` 以上Python代码片段展示了如何基于给定的纬度`lat`和经度`lon`执行由WGS84向UTM坐标的转变操作[^2]。请注意，在实际编程环境中还需要考虑更多细节比如异常处理等。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

GIS思维

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值