前言
在新冠疫情防控过程中,能够及早的检测和排查出病毒感染者将使疫
情能够得到控制从而降低损失。本文通过分析新冠病毒的传播方式及人群
聚居地的动态,建立了相关数学模型,研究了不同区域、不同职业属性的
人群之间的接触规律。
对于问题一
对于问题二
关键词: 综合评价法 熵值法
一、问题重述
当前,新冠病毒的传播特征是传播速度快,轻症、无症状者比例高,且轻
症、无症状者具有传染能力。考虑疫情防控常态化需求,需要长期对一个地区
的人员进行监测。可以采用抽取部分人员进行核酸检测的方法,尽快检测出群
体中是否存在新冠病毒携带者。
问题 1.
对一个群体设计监测方案,以达到在尽量少的检测人次条件下,尽
早地发现病毒携带者这一目的,可考虑不同属性的群体,监测方案不同等。分
别对某一城市(总人数为
600
万)和某一高校(总人数为
5
万)进行建模分析。
问题 2.
若一个群体是由若干小群体构成,小群体可以按照不同特征进行分
类,需要考虑群体内部的影响方式和群体之间的影响方式不同,如何设计监测
方案,以达到上述目的。
二、问题分析
问题一
为了尽早的发现病毒携带者,首先需要对群体中所有人与病毒传播
方式进行分析。
根据目前全球对外公布的新冠资料表明病毒的传播是人传人,即本文只
考虑在同一时间、空间有交集的人群才会有被感染的可能性。
对于群体中的不同个体,每天所接触的人数即所接触的人是否具有代表
性都是需要对其进行量化,只要确保所选的个体既能有效接触整个群体中的大
部分人,又能及时反应人群是否有被感染的情况。
根据目前对外公布的新冠资料,病毒初期不会被发现彼此所确定个体的
核酸次数也是决定快速发现新冠病毒携带者的主要因素。综上分析要解决目标
问题首先要对整个群体中所有人按照职业、平均每天接触人数和平均接触时长
来进行进行统计。其中各指标表示行业中对新冠病毒传染的影响指标,收集相
关数据并建立综合评价模型。
问题二
根据问题一得到对全体人员的检测方案,通过上述检测方案只能得
到新冠病例携带者存在。要检索到第一例病毒携带者则需要根据不同小群体之
间的接触人数及对应的时间确定待检测人员的数量,具体分析如下:
1.
确定目前阳性病例最大的病毒潜伏期,本文为了全面的对可能出现的第
一代病毒携带者所有人员进行检测,潜伏期按照目前我国对外公布的最大值来
处理。
2.
对已发现的阳性人员上一代的人员分两部分来源进行检索。第一部分同
类群体所接触的人员,第二部分则是阴性病例所属群体所接触的人员,以此来
确定所有可能存在第一代病毒携带者人员。
3.
第一代病毒携带者自身的特点,在发现阳性人员时,自身也是阳性,同
时与前阴性病例关联的所有人员接触时间间隔最长。
4.
每次检测人员使用核酸检测的时间相同,综上通过问题一所建立的模型
得到结果,设计第一代病毒携带者检索算法即可。
模型假设
1.
仅考虑同一时间、同一地点中的人之间的接触;
2.
在建立城市监测模型时不考虑学校学生的影响;
3.
在建立学校监测模型时不考虑校外人群与校内人群间接触的影响;
4.
整个过程中城市处于正常经营状态,而学校处于封闭状态,其内人员与
外界无接触;
5.
只考虑人与人之间的接触传播,不考虑病毒依附于其它介质对人的传播;
6.
新冠病毒对所有人的感染能力相同;
四、符号说明

五、模型准备
平均每天接触人数
将每人平均每天接触的人数作为研究对象,探究其对传播的影响。
假设某职业员工平均每天在日常经营中接触到的人数为
n
,
其离开家之前为
0
。其在去往工作地点过程中可能从接触到的人数为
∆
n
总结提示:这里对文章进行总结:
六、模型建立与求解
问题一模型建立与求解
0.2.1
各指标的介绍
平均每天接触人次(按行业分类)
设
ϑ
行业每天接触人数为
x
1
i
平均每天接触人次的复杂程度,即各行业的数量
设
ϑ
行业每天接触人数复杂程度为
x
2
i
平均停留时长,即被感染的风险大小
4
设
ϑ
行业每天接触人群停留时长为
x
3
i
数据标准化
首次判断上述指标哪些是正向指标,哪些是反向指标
选取表转化模型
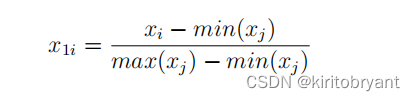
反向
权重的确定
主观权重
[
层次分析法,序关系分析法
]
客观权重
[
熵权法,基于标准差和平均差最大化
]
0.2.3
模型求解
若对总人数
600
万的城市
通过查阅各市的统计年鉴统计各行业的就业人数,明确行业数量
统计上述
3
项指标(部分数据找不到,可根据收入进行估计)
仅用权重确定模型各指标权重

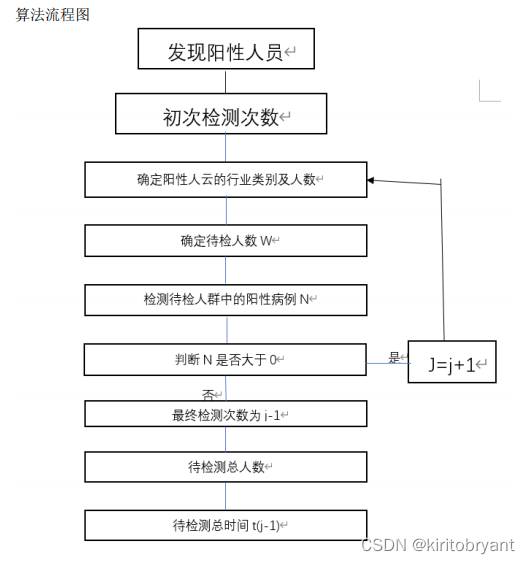
由问题一所得到的数据可知第
i
歌行业平均每天接触人数为
x
j
。最大检测时
间为
T
,对于初始状态,检测次数为
u
= 1
,对应的待检人数
N
uj
=
x
j
[
T
−
t
u
+1]

























 6529
6529

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










