特殊矩阵的主要形式有:
(1)对称矩阵
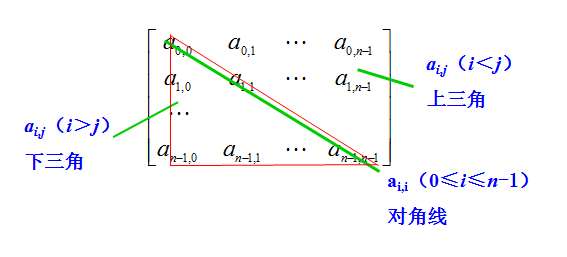
(2)上三角矩阵/下三角矩阵
(3)对角矩阵
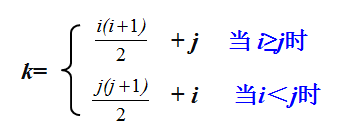
(1)对称矩阵
(2)上三角矩阵/下三角矩阵
(3)对角矩阵
它们都是方阵,即行数和列数相同。
一、对称矩阵的压缩存储
若一个n阶方阵A[n][n]中的元素满足a i,j=a j,i(0≤i,j≤n-1),则称其为n阶对称矩阵。
由于对称矩阵中的元素关于主对角线对称,因此在存储时可只存储对称矩阵中上三角或下三角中的元素,使得对称的元素共享一个存储空间。
这样,就可以将n2个元素压缩存储到n(n+1)/2个元素的空间中。以行序为主序存储其下三角+对角线的元素。
n2个元素←→ n(n+1)/2个元素
A[0..n-1,0..n-1] ←→ B[0..n(n+1)/2-1]
a[i][j] ←→ b[k]
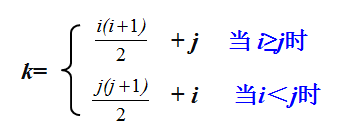
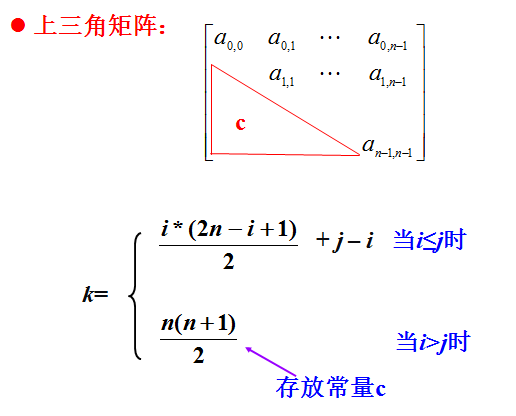
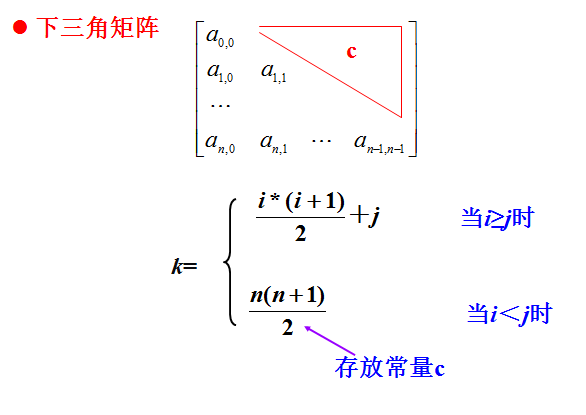
二、三角矩阵的压缩存储


三、 对角矩阵的压缩存储
若一个n阶方阵A满足其
所有非零元素
都集中在以主对角线为中心的
带状区域中
,则称其为
n阶对角矩阵
。
其主对角线上下方各有b条次对角线,称b为矩阵半带宽,(2b+1)为矩阵的带宽。
对于半带宽为b(0≤b≤(n-1)/2)的对角矩阵,其|i-j|≤b的元素ai,j不为零,其余元素为零。
下图所示是半带宽为b的对角矩阵示意图。
A ←→ B
a[i][j] ←→ b[k]
当b=1时称为三对角矩阵。其压缩地址计算公式如下: k=2i+j

























 1009
1009

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








