二维空间下椭圆基本方程为
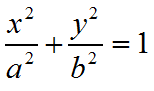 (1)
(1)
这个是我们大家都熟知的,但是,如果背景空间不是二维空间,而是N维欧式空间中的椭圆,其表达式应该是什么样式的?
为了对这个问题论证比较严格,在下述过程中采用了微分几何中的一些思想,而且用了微分几何中的一些标记。但是如果没有微分几何的基础也能够看懂。这个问题的本质在于坐标变换。只要对坐标变换有一些了解,理解以下内容并没有难度。
椭圆方程写为参数方程形式为:
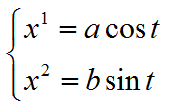 (2)
(2)
其中,x上标1和2,本质意思是表示在第一轴和第二轴上的分量
这个参数方程可以看做是以下参数方程的简写:
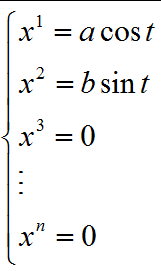 (3)
(3)
对原理不要求理解的可以忽略双线内的这几段,对方法掌握无影响
《======================================================
然后(2)可以写为另一种等价的形式:
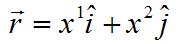 (4)
(4)
(3)按照同样的方法也可以写为同样的形式:
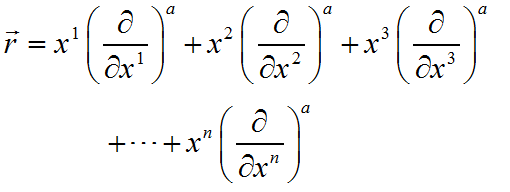 (5)
(5)
其中,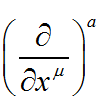 是微分几何中对于坐标基矢的表示,对应于我们在三维直角坐标系中习惯用的
是微分几何中对于坐标基矢的表示,对应于我们在三维直角坐标系中习惯用的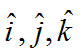 ,由于是N维欧式空间,用
,由于是N维欧式空间,用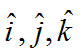 只能表示三维,不方便,所以直接用微分几何的符号,只需记住,这两组符号是等价的即可。
只能表示三维,不方便,所以直接用微分几何的符号,只需记住,这两组符号是等价的即可。
================================================================================》
于是,(4)可以将坐标基矢全部省略,写为
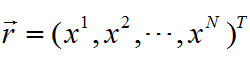 (6)
(6)
其中,
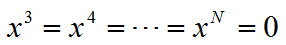 (7)
(7)
在新的坐标系中,椭圆在各个坐标轴方向的分量为
(8)
《============================
也就是
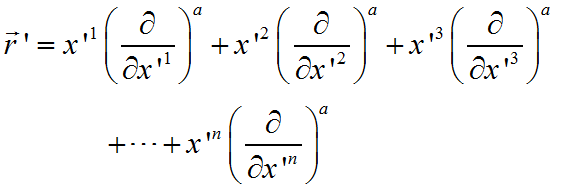 (9)
(9)
===================================》
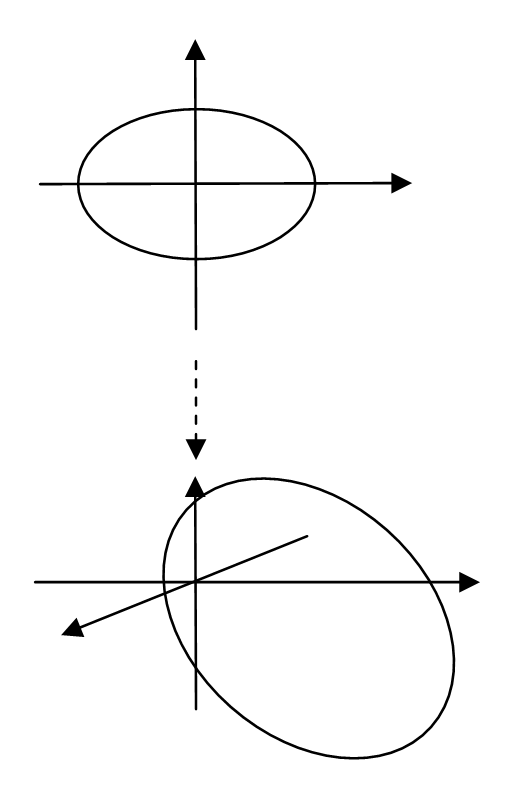
两组坐标矢量之间的关系,对应的一组变换矩阵,外加一个平移矢量。这个变换矩阵可以是奇异的,也可以死非奇异的,都可以。变换示意图如下:
然后,带 ' 的x和不带 ’的x之间的关系可以表示为:
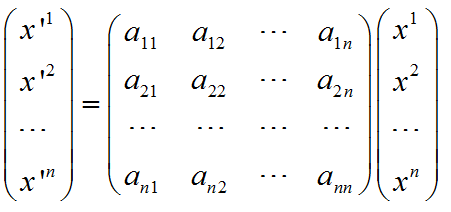 (10)
(10)
于是,根据(7)可以得到,
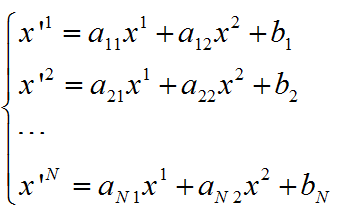 (11)
(11)
将(2)带入得
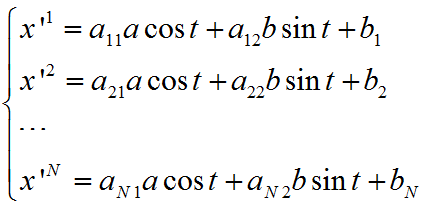
(12)
整理得
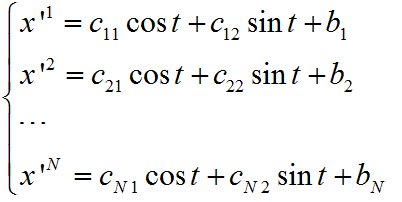 (13)
(13)
或是
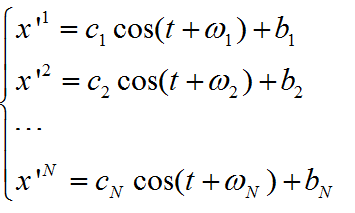 (14)
(14)
所以,得到结论,高维空间中椭圆方程为普通形式为(13)或者(14).
但有点需要注意, (13)或者(14) 得到的结果并不一定一定是椭圆,还可能是椭圆的两种退化形式,椭圆的偏心率e所在的范围是(0,1),不包括边界,所以两种退化形式,一个是偏心率e=0时,即为圆,另一个是偏心率e=1,退化为线段。是否椭圆,还有一些判别公式,相关理论还没整理完成,暂时不论证了。
该套方法可以将低维空间中任意函数曲线扩展到高维空间中,并不只限于椭圆
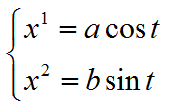
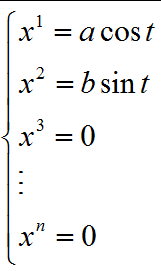
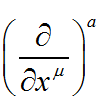
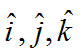
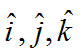
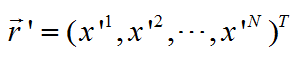








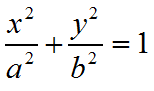
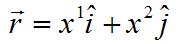
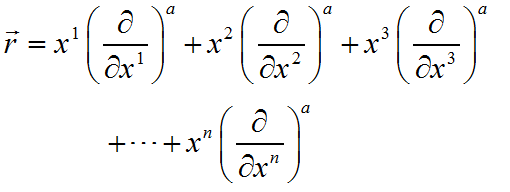
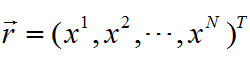
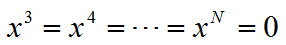
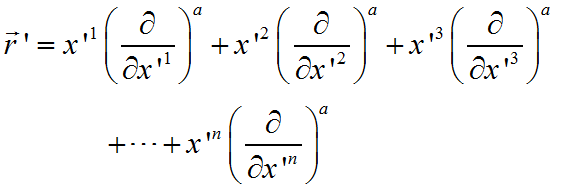
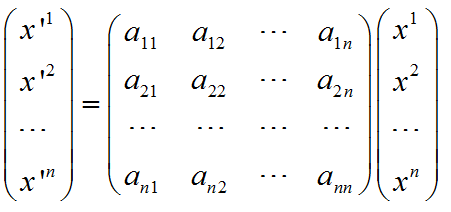
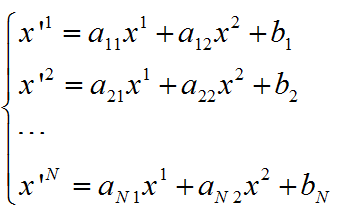
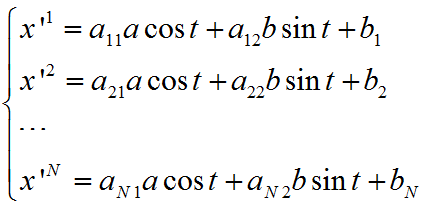
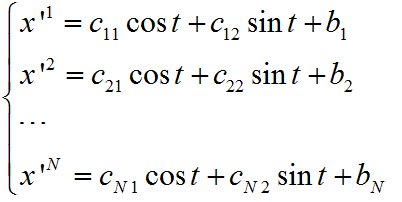
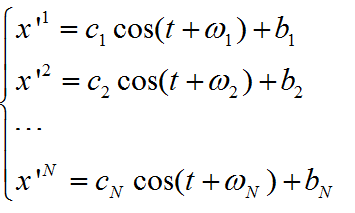

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








