除法运算对应的汇编指令分为有符号idiv和无符号div两种。除法指令的执行周期较长,效率也低,所以编译器想尽办法用其他运算指令代替除法指令。C++中的除法和数学中的除法不同。在C++中,除法运算不保留余数,有专门的的求取余数的运算(运算符为%),也称为取模运算。对于整数除法,C++的规则是仅仅保留整数部分,小数部分完全舍弃。
在C语言中
两个无符号数相除,结果为无符号数;
两个有符号数相除,结果为有符号数 ;
如果有符号数和无符号数混除,其结果是无符号的;
(有符号数的最高位(符号位)被作为数据位对待,然后作为无符号数参与运算)
怎么取整?
1》向下取整:存在问题[-a/b]!=-[a/b]
2》向上取整:存在问题[-a/b]!=-[a/b]
3》向零取整:[-a/b]=[a/-b]=-[a/b]
三种方式中,明显第三中比较好,所以在C和其他高级语言中,对整数除法规定为向零取
整。也称为“截断除法”
为什么
(1)printf("8%%-3=%d\n",8%-3);
(2)printf("-8%%-3=%d\n",-8%-3);
(3)printf("-8%%3=%d",-8%3);
依次输出 2,-2,-2?
记,被除数为a,除数为b,余数为r,商为q
a = b * q + r
又因为整数除法向0取整
q(1)= 8/-3=-2
q(2)=-8/-3=2
q(3)=-8/ 3=-2
故:
r(1)= 8-(-3)*(-2)= 2
r(2)=-8-(-3)* 2 =-2
r(3)=-8- 3 *(-2)=-2
编译器是怎么对除法进行优化的?
如果除数是变量,则只能使用除法指令。
如果除数是常量,就有了优化的余地
<1>除数为2的幂
//C++
nVarOne/2
//反汇编
cdq//如果eax的最高位为1,置edx为0xFFFFFFFF,如果eax的最高位为0,置edx为0x00000000
sub eax,edx//C语言是向0取整,而sar是向右移位(相当于想下取整),这条语句就是在eax为负数时,对eax加1(-0XFFFFFFFF相当于加1),在eax为正数时eax不变,这样就实现了向零取整,避免的分支产生。
sar eax,1//对有符号数右移1位
<2>除数非2的幂
我们来看个例子,IDA显示结果
_main proc near
arg_0 = dword ptr 4
mov ecx,[esp+arg_0]//被除数
mov eax,38E38E39h //38E38E39h称为Magic常量,为(2^n)/o的结果,由编译器算出
imul ecx //x* ((2^n)/o)
sar edx,1 //直接使用edx相当于右移32位,总共右移33位,即x*((2^32)/o)*(1/(2^33))
mov eax,edx //将结果放入eax中
shr eax,1Fh //无符号移位,右移31位(为什么呢,看下面)
push offset Format ;"%d"
call _printf
add esp,8
retn
_main endp
在C语言中
两个无符号数相除,结果为无符号数;
两个有符号数相除,结果为有符号数 ;
如果有符号数和无符号数混除,其结果是无符号的;
(有符号数的最高位(符号位)被作为数据位对待,然后作为无符号数参与运算)
怎么取整?
1》向下取整:存在问题[-a/b]!=-[a/b]
2》向上取整:存在问题[-a/b]!=-[a/b]
3》向零取整:[-a/b]=[a/-b]=-[a/b]
三种方式中,明显第三中比较好,所以在C和其他高级语言中,对整数除法规定为向零取
整。也称为“截断除法”
为什么
(1)printf("8%%-3=%d\n",8%-3);
(2)printf("-8%%-3=%d\n",-8%-3);
(3)printf("-8%%3=%d",-8%3);
依次输出 2,-2,-2?
记,被除数为a,除数为b,余数为r,商为q
a = b * q + r
又因为整数除法向0取整
q(1)= 8/-3=-2
q(2)=-8/-3=2
q(3)=-8/ 3=-2
故:
r(1)= 8-(-3)*(-2)= 2
r(2)=-8-(-3)* 2 =-2
r(3)=-8- 3 *(-2)=-2
编译器是怎么对除法进行优化的?
如果除数是变量,则只能使用除法指令。
如果除数是常量,就有了优化的余地
<1>除数为2的幂
//C++
nVarOne/2
//反汇编
cdq//如果eax的最高位为1,置edx为0xFFFFFFFF,如果eax的最高位为0,置edx为0x00000000
sub eax,edx//C语言是向0取整,而sar是向右移位(相当于想下取整),这条语句就是在eax为负数时,对eax加1(-0XFFFFFFFF相当于加1),在eax为正数时eax不变,这样就实现了向零取整,避免的分支产生。
sar eax,1//对有符号数右移1位
<2>除数非2的幂
这种情况编译器处理比较复杂,我们先来看一个数学推导
我们来看个例子,IDA显示结果
_main proc near
arg_0 = dword ptr 4
mov ecx,[esp+arg_0]//被除数
mov eax,38E38E39h //38E38E39h称为Magic常量,为(2^n)/o的结果,由编译器算出
imul ecx //x* ((2^n)/o)
sar edx,1 //直接使用edx相当于右移32位,总共右移33位,即x*((2^32)/o)*(1/(2^33))
mov eax,edx //将结果放入eax中
shr eax,1Fh //无符号移位,右移31位(为什么呢,看下面)
add edx,eax //其实这个移位是为了得到符号位,如果结果为正,add edx,eax
//相当于edx+0;如果结果为负,相当于edx + 1(目的也是向零取整)
push edx //edx为最终运算结果push offset Format ;"%d"
call _printf
add esp,8
retn
_main endp
<3>除数为负
除数为负编译器优化方案更加复杂,我们先跳过,用到再回过头看。








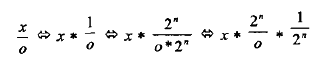
















 6123
6123

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








