线性回归模型

yicheng_01

已于 2023-02-01 22:55:54 修改

阅读量7k

点赞数 5

于 2021-10-13 21:50:51 首次发布

本文链接：https://blog.csdn.net/l1232323/article/details/120748438

版权

线性回归是最简单的机器学习模型，也是最基础最重要的分析工具，易于实现。本文将将简单讲述线性回归、最小二乘法和梯度下降三种算法。

1.线性回归方程(OLS)

对一个给定的训练集数据，线性回归的目标是找到与这些数据最相符的线性函数。该算法可用于预测、分类等问题，回归分析可以分为三个部分：（1）识别重要变量（2）判断相关性的方向（3）估计回归系数

首先，数据可以分为时间序列数据、面板数据和横截面数据三类。

（1）时间序列数据：对同一对象在不同时间连续观察得到的数据；

（2）横截面数据：在某一时刻所收集的不同对象的数据；

（3）面板数据：横截面数据与时间序列数据综合起来的一种数据资源。

对于不同类型的数据需要使用不同的回归模型，具体如下：

数据类型	常见建模方法
时间序列数据	多元线性回归
横截面数据	移动平均、指数平滑、ARIMA、GARCH、VAR、协积
面板数据	固定效应和随机效应、静态面板和动态面板

下面我们介绍一下线性回归模型。

一般地，线性回归模型函数形式为：

$h_w,_b(x)=\sum_{i=1}^{n}w_ix_i+b_i=w^Tx+b$

其中， $w\in R^n$ 与 $b\in R$ 为模型参数，即回归系数。我们做一下变换：

$w=(b,w_1,w_2,...,w_n)^T$ , $x=(1,x_1,x_2,...,x_n)^T$ .

此时，函数形式为：

$h_w(x)= \sum_{i=0}^{n}w_ix_i=w^Tx$

其中， $w\in R^{n+1}$ ,通过训练模型确定参数 $w$ ，再将新的数据输入进行预测。

2.最小二乘法(OLS)

线性回归模型中通常用均方误差(MSE)作为损失函数，假设训练集D中有m个样本，其损失函数为：

$J(w)=\frac{1}{2m}\sum_{i=1}^{m}(h_w(x_i)-y_i)^2=\frac{1}{2m}\sum_{i=1}^{m}(w^Tx-y_i)^2$

模型的训练目标是找到使损失函数最小化的 $w$ ,式中的 $\frac{1}{2}$ 无实际含义，只是为了优化求导时方便。

损失函数 $J(w)$ 的最小值就是其极值点，可先求 $J(w)$ 对 $w$ 的梯度并令其为0，再求解 $w$ .

$J(w)$ 的梯度：

$\bigtriangledown J(w)=\frac{1}{2m}\sum_{i=1}^{m} \frac{\partial }{\partial w}(w^Tx_i-y_i)^2=\frac{1}{m}\sum_{i=1}^{m}(w^Tx_i-y_i)x_i$

可以引入

$X=\begin{bmatrix} 1, &x_1_1, & x_1_2 &\cdots &x_1_n \\ 1, & x_2_1, &x_2_2 & \cdots &x_2_n \\ \vdots &\vdots &\vdots & \ddots &\vdots \\ 1,& x_m_1, &x_m_2 &\cdots &x_m_n \end{bmatrix}=\begin{bmatrix} x_1^T\\x_2^T \\\vdots \\ x_m^T \end{bmatrix}$ ,

$y=\begin{bmatrix} y_1\\ y_2 \\\vdots \\y_m \end{bmatrix}$ ,

$w=\begin{bmatrix} b\\w_1 \\w_2 \\ \vdots \\w_n \end{bmatrix}$

则梯度计算公式可写为:

$\bigtriangledown J(w)=\frac{1}{m}X^T(Xw-y)$

再令梯度为 0 ，得：

$\hat{w}=(X^TX)^{-1}X^Ty$

其中， $\hat{w}$ 为损失函数最小的 $w$ . 式中的 $X^TX$ 是满秩的，但是 $X^TX$ 不总是满秩的，只是会存在多个 $\hat{w}$ ，这时可以引入正则化项。

以上求解最优的 $w$ 的方法就是最小二乘法。

3.梯度下降(GD)

很多机器学习模型的最优化参数不能通过最小二乘法这种“闭式”方程求得，这时就需要用到“迭代优化”的方法，即每次根据当前情况做出一点点微调，反复迭代调整，直到达到最优或接近最优时才停止，其中应用最广泛的迭代优化方法就是梯度下降法。梯度下降就是逐步调整参数，使得损失函数最小。

损失函数最小化的过程示意图如下：

图1

每次下降都是沿着函数值下降最快的方向，梯度下降算法可描述为：

（1）根据当前参数 $w$ 计算损失函数梯度 $\bigtriangledown J(w)$ ；

（2）沿着梯度反方向 $-\bigtriangledown J(w)$ 调整 $w$ ,调整的大小称为步长，由学习率 $\eta$ 控制，其公式为：

$w:=w-\eta\bigtriangledown J(w)$

（3）反复执行上述过程，直到梯度为 0 或损失函数降低小于阈值，此时算法已收敛。

另外，应用梯度下降算法需要考虑几种情况。

3.1超参数 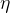$\eta$ 的选择

如果 $\eta$ 过大，则有可能出现接近最小值时又跳跃到函数更大的值上的情况，即越过最小值点，如图2所示；而如果 $\eta$ 过小，则接近最小值的速度会很慢，算法收敛速度过慢，会导致模型训练时间过长，如图3.

图2 图3

3.2局部最小值

梯度下降算法可能会收敛于局部最小值，而非全局最小值。如果起始点位于局部最小值的左侧，算法很有可能收敛于局部最小值，如图4

图4

这是因为，梯度算法的每一步都是基于整个训练集X计算梯度的，并且每次都使用整批训练样本计算梯度，当训练集过大时，算法运行速度会很慢。

设学习率为 $\eta$ ，随机梯度下降算法的参数更新公式为:

$w:=w-\eta\frac{1}{m}X^T(X^w-y)$

3.3随机梯度下降和小批量梯度下降

（1）随机梯度下降

随机梯度下降是与批量随机下降相反的极端情况，每步只用一个样本来计算梯度。

随机梯度下降算法梯度公式为：

$\bigtriangledown J(w)=(w^Tx_i-y)$

设学习率为 $\eta$ ，随机梯度下降算法的参数更新公式为：

$w:=w-\eta(w^Tx_i-y_i)x_i$

通常随机梯度下降收敛时，参数 $w$ 是足够优的，但不是最优的。但当损失函数很不规则时，即存在多个局部最小值时，更有可能会跳过局部最小值，最终接近全局最小值。随机梯度下降的每一轮训练前通常都要随机打乱训练集。

（2）小批量梯度下降

小批量梯度下降是介于批量梯度下降和随机梯度下降之间的方案，每一步使用一小部分训练集来计算梯度。

设一小批样本的数量为N,小批量梯度下降算法的梯度计算公式为：

$\bigtriangledown J(w)=\frac{1}{N}\sum_{i=k}^{k+N}(w^Tx_i-y_i)x_i$

设学习率为 $\eta$ ,小批量梯度算法的参数更新公式为:

$w:=w-\eta\frac{1}{N}\sum_{i=k}^{k+N}(w^Tx_i-y_i)x_i$

小批量梯度下降算法应用时可以根据情况指定 $N$ 值。

以上就是线性回归模型的简单介绍，之后会更新使用python分别实现OLS回归和GD回归，后续还会更新一些算法，小伙伴们可以关注一下哦！

yicheng_01

关注

5
点赞
踩
19

收藏

觉得还不错? 一键收藏
2
评论
线性回归模型

线性回归是最简单的机器学习模型，也是最基础最重要的分析工具，易于实现。本文将将简单讲述线性回归、最小二乘法和梯度下降三种算法。1.线性回归模型对一个给定的训练集数据，线性回归的目标是找到与这些数据最相符的线性函数。可进行预测、分类，回归分析可以分为三个部分：（1）识别重要变量（2）判断相关性的方向（3）估计回归系数首先，数据可以分为时间序列数据、面板数据和横截面数据三类。（1）时间序列数据：对同一对象在不同时间连续观察得到的数据；（2）横截面数据：在某一时刻所收集的不同对象的数据；（
复制链接

扫一扫