COMSOL案例学习（2）：非定常圆柱绕流三维模型

✅作者简介：大家好我是Xlong，一枚正在学习COMSOL、Python的工科研究僧
📃个人主页: Xlong的个人博客主页
🔥系列专栏：COMSOL学习
💖如果觉得博主的文章还不错的话，请👍支持一下博主哦🤞

案例链接：

非定常圆柱绕流三维模型https://cn.comsol.com/model/unsteady-3d-flow-past-a-cylinder-73041

目录

一、案例简介

二、模型定义

2.1 几何模型

2.2 流入速度分布

2.3 流型的特征

2.4 升力系数和曳力系数

 三、模拟结果

3.1 升力系数随时间的变化情况

 3.2 曳力系数随时间的变化情况

 3.3 t=1~8 s时绘制的流线

 四、知识点总结

4.1 流体离散化中的P2+P2形、P2+P1形、P1+P1形函数

4.2 自动时间步进的广义α方法、BDF方法（向后差分公式）

4.3 将流动区域划分为多个子域

---

一、案例简介

        圆柱绕流是计算流体力学（CFD）中常见的算例。所谓“非定常”指流体的流动状态随时间而改变。若流动状态不随时间而改变，则为“定常流动”。现实生活中，流体的流动几乎都是非定常的。

        在本案例中，主要研究了绕圆柱体0到8秒（0~8s）内的不可压缩三维非定常流动，计算了升力系数和曳力系数，并绘制了流线。

二、模型定义

2.1 几何模型

        几何形状是半径为的圆柱体，其轴与轴平行，位于长方体内（xc,yc,0）处，如图1所示，显示的是 = 0.05m、 = 2.5m、 = 0.5m且 = 0.5m、 = 0.2m所对应的几何图形。

图1 几何模型：放置在长方体中的圆柱体

2.2 流入速度分布

        本例中的流体为不可压缩的牛顿流体，其运动粘度为。流入速度分布随时间变化：

2.3 流型的特征

        流型的特征用雷诺数表示，定义为：

        

        其中，是流体密度，表示自由流的平均流速，是圆柱直径，是流体动力粘度。

        

2.4 升力系数和曳力系数

        （1）升力系数：一个无量纲量，指物体所受到的升力与流体动压和参考面积的乘积之比。

        （2）曳力系数：一个无量纲量，一般指流体阻力系数，指一个物体在流体（液体或气体）中和流体有相对运动时，物体会受到流体的阻力。阻力的方向和物体相对于流体的速度方向相反，其大小和相对速度的大小有关。

        在本例中，升力系数和曳力系数是时间的函数：

        其中，和表示曳力和升力，是投影面积 。

 三、模拟结果

3.1 升力系数随时间的变化情况

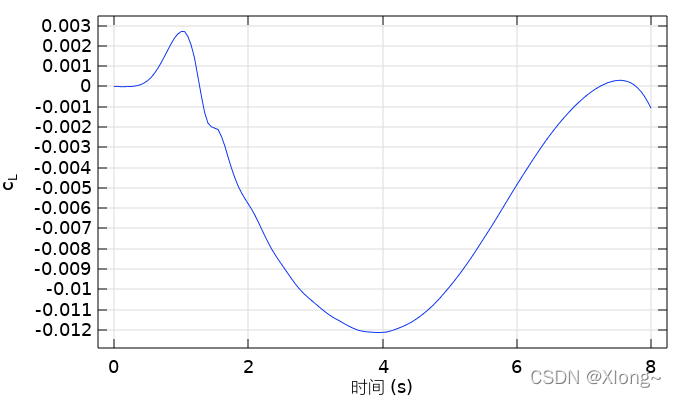
 图2  升力系数随时间的变化曲线

 3.2 曳力系数随时间的变化情况

  图3  曳力系数随时间的变化曲线

 3.3 t=1~8 s时绘制的流线

   图4  t=1s时的流线

    图5  t=2s时的流线

     图6  t=3s时的流线

      图7  t=4s时的流线

       图8  t=5s时的流线

        图9  t=6s时的流线

         图10  t=7s时的流线

       图11  t=7.95s时的流线

 四、知识点总结

4.1 流体离散化中的P2+P2形、P2+P1形、P1+P1形函数

        （1）离散化的含义是什么？

        详细内容见链接         离散化的含义是什么？它对网格和求解结果有什么影响？ - 知乎

        （2）P2+P2与P2+P1、P1+P1相比，前者更稳健且更准确。

4.2 自动时间步进的广义α方法、BDF方法（向后差分公式）

                                           瞬态求解器提供三种不同的时间步进方法：广义\alp方法、隐式向后差分公式以及显示龙格-库塔系列方法。

        （1）隐式向后差分公式：一种使用向后差分公式的隐式求解器，其精度在一阶到五阶之间变化，以稳定性而著称。（详细内容请见链接）      

        （2）广义α方法：与二阶向后差分公式类似，但底层技术不同。（详细内容请见链接）

        （3）显示龙格-库塔系列方法：最适用于“常微分方程组”，但对于涉及“偏微分方程”的问题，往往不是很有效。（详细内容请见链接）

4.3 将流动区域划分为多个子域

        在本例中，通过PDF教程中的步骤进行操作将流动区域划分为多个子域，这样可在远离圆柱体的区域使用较粗化的网格，节省计算资源。

持续更新中.................................................................

原创不易，各位看官请随手点下Follow和Star，感谢！！！