代理模型+多目标优化算法之基于克里金(kriging)模型代理模型和MOEA-D多目标优化算法案例

基于克里金（Kriging）模型代理和多目标优化算法（MOEA-D）的案例研究

一、引言

在复杂的工程和科学问题中，代理模型和多目标优化算法的应用日益广泛。其中，代理模型用于近似实际复杂的行为，而多目标优化算法则用于寻找多个目标之间的最优解。本文将着重讨论基于克里金（Kriging）模型的代理模型和MOEA-D（多目标进化算法）的联合应用，并分析其在一个具体案例中的实践效果。

二、克里金（Kriging）模型代理模型

克里金模型是一种基于统计的代理模型，常用于地统计和插值问题中。其基本思想是利用空间中的已知点数据来预测未知点的值。在多目标优化问题中，克里金模型可以作为决策变量和目标函数之间的桥梁，为复杂提供一个简化的代理表示。

在案例中，克里金模型被用来构建一个关于产品设计参数与产品性能之间关系的代理模型。设计师通过改变产品设计的参数（如材料、尺寸等），观察产品的性能指标（如强度、重量等），并将这些数据输入到克里金模型中。模型通过学习这些数据，能够预测新的设计参数下产品的性能。

三、MOEA-D多目标优化算法

MOEA-D（多目标进化算法）是一种用于解决具有多个目标的优化问题的算法。与传统的单目标优化不同，多目标优化问题需要考虑多个相互冲突的目标，寻找的是能同时满足这些目标的最佳折中解。

在案例中，MOEA-D算法被用于寻找最佳的产品设计参数组合。这些参数不仅要满足产品的性能要求（如强度、耐用性等），还要考虑制造成本、材料利用率等经济因素。MOEA-D算法通过模拟自然进化过程，在多个目标之间进行权衡和折中，最终找到一个最优的解集。

四、案例分析

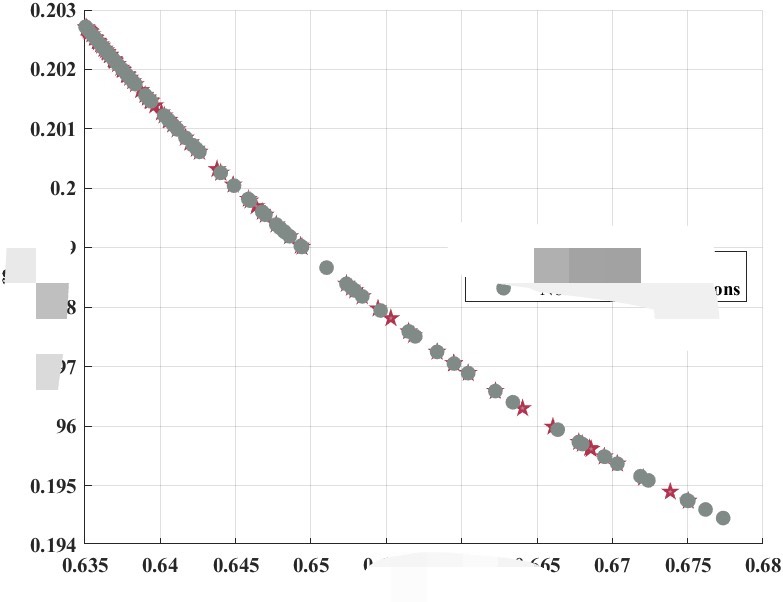
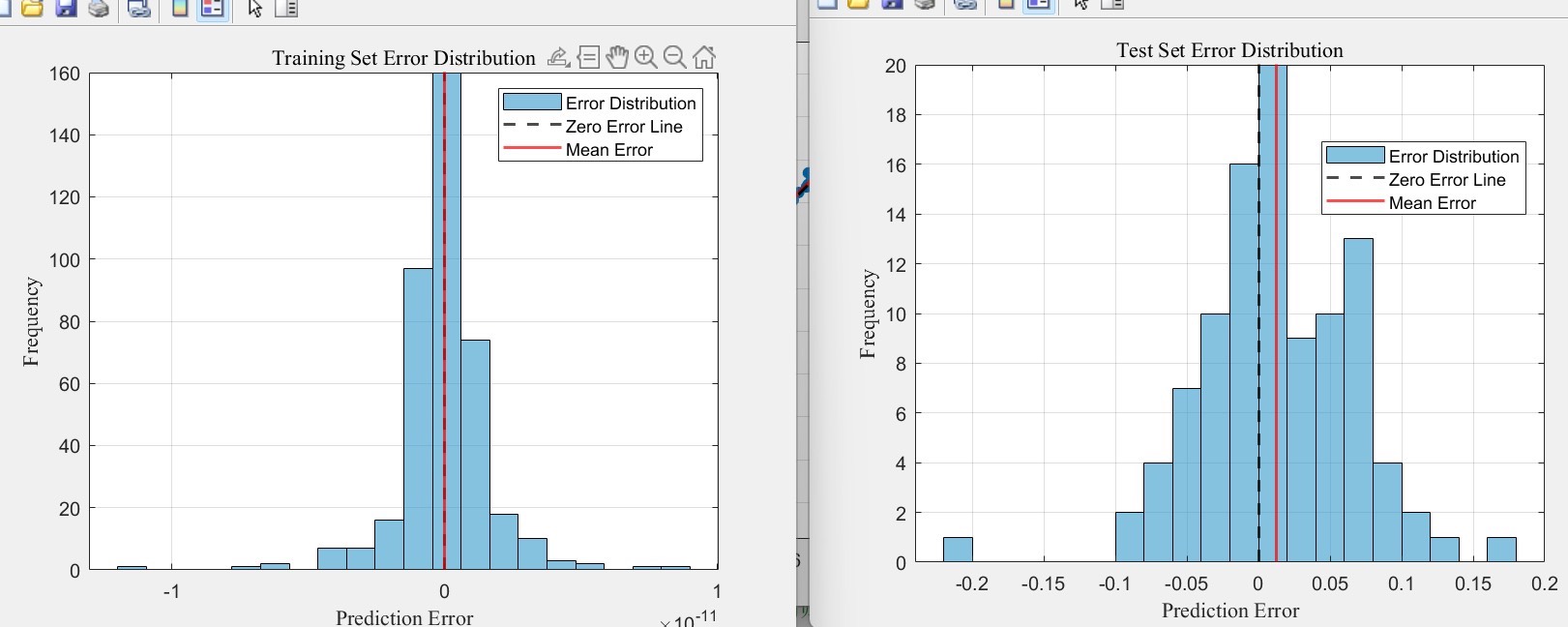
在这个案例中，我们首先使用克里金模型构建了一个关于产品设计参数与产品性能的代理模型。然后，我们利用MOEA-D算法在多个目标（如性能、成本、材料利用率等）之间进行优化。通过反复迭代和优化，我们找到了一个最佳的参数组合，使得产品能够在满足性能要求的同时，实现成本和材料利用率的最大化。

通过将克里金模型和MOEA-D算法结合起来，我们能够在不进行实际试验的情况下，快速地找到最佳的解决方案。这不仅节省了大量的时间和成本，还提高了解决方案的质量。

五、结论

本文介绍了基于克里金（Kriging）模型的代理模型和MOEA-D多目标优化算法在案例中的应用。通过结合这两种技术，我们能够有效地解决具有多个目标的复杂优化问题。这不仅提高了解决方案的质量，还降低了解决方案的成本和时间。随着技术的发展和方法的不断完善，这种结合代理模型和多目标优化算法的方法将在更多的领域得到应用。
代理模型+多目标优化算法之基于克里金(kriging)模型代理模型和MOEA-D多目标优化算法案例