数据结构::浅析平衡二叉树

【为什么我们要引入平衡二叉树？】

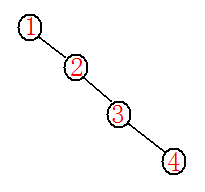
在学习完搜索二叉树后，我们知道搜索二叉树退化了之后，它的样子和单链表很像（如下图），在这种情况下，我们如果进行搜索的话，它的时间复杂度就大大降低了，此时的时间复杂度是O（N）。

因此我们引入了平衡二叉树，它解决了搜索二叉树效率低的缺点

【平衡二叉树（AVL树）】：

1、平衡二叉树的概念：

（首先它是搜索二叉树）要么是空树，要么是具有以下性质的二叉树:

1）左右子树都是平衡二叉树

2）左右子树的高度之差不超过1

3）每个节点都有一个平衡因子，平衡因子的取值范围只能是-1,0,1.

2、平衡因子：

     平衡二叉树中左右子树的高度或者说深度之差，我们可以知道，平衡因子的取值为：-1,0,1.

     说明：我们用平衡因子的大小来判断是不是平衡二叉树

3、节点的定义（结构）：

说明：关于在结构中，多了一个关键值，这个关键值的作用我后面会讲到。

template<class K,class V>
struct AVLTreeNode
{
	K _key;   //关键字
	V _value;  //关键值
	int _bf;   //平衡因子
	AVLTreeNode<K,V>* _left;
	AVLTreeNode<K,V>* _right;
	AVLTreeNode<K,V>* _parent;

	AVLTreeNode(const K& key,V& value)
		:_left(NULL)
		,_right(NULL)
		,_parent(NULL)
		,_key(key)
		,_value(value)
		,_bf(0)
	{}
};

4、平衡二叉树的查找

说明：在查找的时候和搜索二叉树是一样的

Node* Find(const K& key)
	{
		if(_root == NULL)
			return NULL;
		Node* cur = _root;
		while(cur)
		{
			if(cur->_key > key)
			{
				cur = cur->_left;
			}
			else if(cur->_key < key)
			{
				cur = cur->_right;
			}
			else
			{
				return cur;
			}
		}
		return NULL;
	}

5、平衡二叉树的插入（重点）

     我们来看下插入的步骤：

1）首先我们先找到要插入的点

2）找到之后，插入要插入的值

3）此时插入之后，就要进行平衡因子的调节。

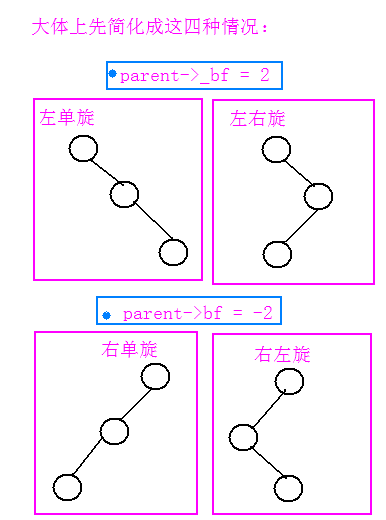
    ** 插入之后，父节点的平衡因子要分的情况：

  

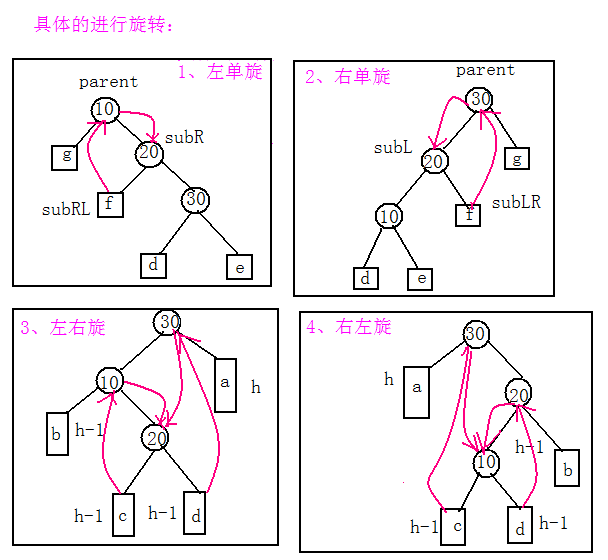
   **旋转的时候又要进行细分，下面我用图解来进行说明：

 

   代码的实现：

    **插入的代码

	bool Insert(const K& key,V& value)
	{
		if(_root == NULL)
		{
			_root = new Node(key,value);
			return true;
		}
		Node* cur = _root;
		Node* parent = NULL;
		//1、先找要插入的点
		while(cur)
		{
			if(cur->_key > key)
			{
				parent = cu