TLDR: 本文介绍超图的基础概念。超图不同于传统图(2-均匀超图),它允许每条边(超边)连接任意数量的顶点,因此能更好地建模复杂的多对多关系。文章内容涵盖了图与超图的定义、超图的对偶性质、边的嵌套性、步行的长度和宽度等核心特性。此外,超图还与拓扑学、二分图、抽象单纯复形等数学结构有深厚的联系。这些概念不仅扩展了传统图论,还在数据分析、复杂系统和拓扑方法中有重要应用。
本文编译自HyperNetx的文档,水平有限,如有任何疏漏错误请参见原文。总觉得需要具体的例子才能理解超图的实际应用,如果看完了和我一样,还是一脸迷惑,一知半解,怀疑人生,那算是正常发挥。

超图(hypergraph)
网络科学(Network Science)基于图(graph)的概念,它是一种描述实体之间连接的系统。一个图包含两个基本部分:一个通常是有限的元素集合,称为顶点(vertices)。给定两个顶点u 和v,边e={u,v} 表示顶点u和v之间存在连接。通常,我们可以使用布尔邻接矩阵(adjacency matrix)来表示图,其中矩阵元素A[i,j]为1表示顶点i和j在图中是连接的;或者使用关联矩阵(incidence matrix)来表示,矩阵I[i,j]为1表示顶点i在边j中。
注:这里的图和超图使用的是简化的概念,即它们是有限的、无环的、简单的、连通的,并且没有空的超边、孤立的顶点、标签、权重或属性。
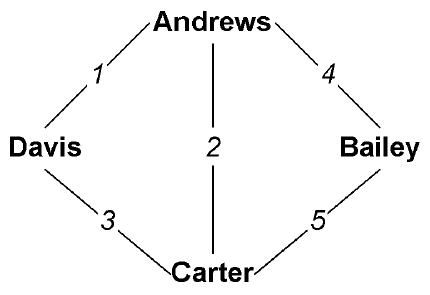
一个图的例子,数字表示边的ID
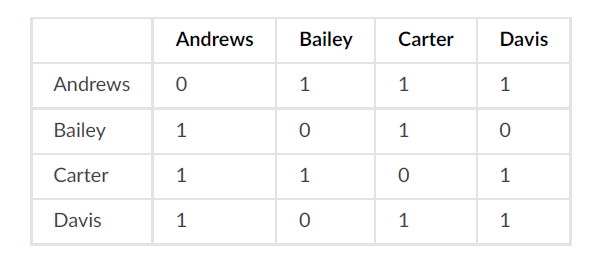
用邻接矩阵表示:
关联矩阵表示:
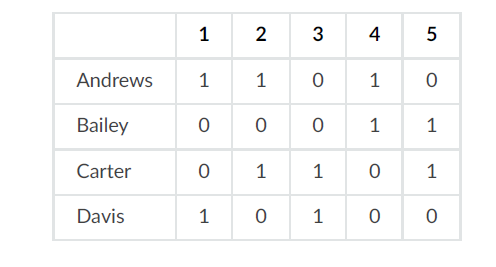
在关联矩阵中,每列必须精确包含两个1,因为这里每条边连接两个顶点。而超图放宽了这一限制,在超图中,超边是任意大小的顶点子集。当超边的大小为 𝑘时,我们称其为 𝑘-边。例如,2-边是普通图中的边,而单一顶点构成的集合、3-边、4-边等都是超图中的边。因此,如果一个超图的每条边都是2-边,那么它就是一个图,我们称这样的超图为2-均匀超图(2-uniform)。图实际上是超图的特殊形式,即2-均匀超图。
一个超图的例子,数字表示边的ID:
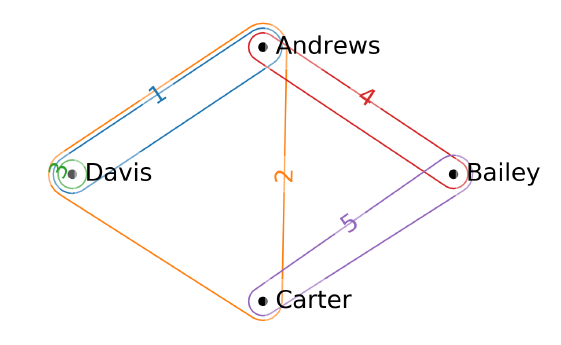
关联矩阵表示:
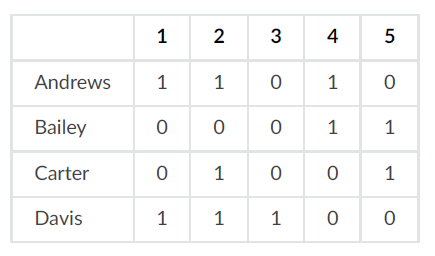
在图示的例子中,图和超图之间有紧密的联系。实际上,这个图是超图的2-截面(2-section)或基础图(underlying graph)。所谓的2-截面是指,当我们只考虑超图中的成对连接(即两两顶点的连接)时得到的图。这意味着我们忽略了超图中涉及多个顶点的复杂连接,只保留那些两两顶点之间的简单连接。
虽然2-截面总是由超图确定的,并且经常作为一种简化表示方式使用,但它几乎从来不能提供足够的信息来完全还原超图的结构。换句话说,2-截面是超图的一部分信息,但远不足以完整描述超图的所有复杂关系。
超图的特性
虽然所有的图 都是 2-均匀的超图,但一般的超图具有一些重要属性,在图中并不存在。这对于熟悉图论的人来说非常重要,以下对于超图是至关重要的问题,在考虑2-均匀超图(即图)时不复存在。
1. 所有超图都有对偶对(Dual Pairs)
每个超图都有一个对应的对偶超图。对偶超图的生成方式是通过将原超图的顶点和边进行交换。具体来说,超图的关联矩阵 I 是一个表示顶点和边之间关系的布尔矩阵,如果你将这个矩阵转置IT,你就会得到另一个超图的关联矩阵,这就是原超图的对偶超图(在图中标记为 H∗)。在对偶超图H∗ 中,原超图的边变成了顶点,原超图的顶点变成了边。
如果一个图 G 是2-均匀超图,那么它的对偶图 G∗ 通常不是2-均匀超图。只有当G是一个简单环或环的组合时,才可能出现对偶也是2-均匀超图的情况。
一个对偶超图的例子:
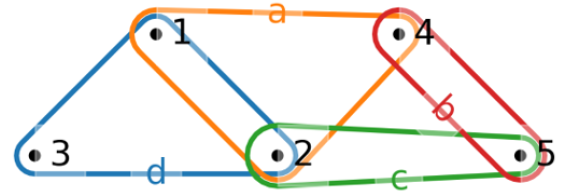
原超图中的顶点a,b,c,d和边1,2,3,4,5交换了位置。
不仅原始超图有2-截面(2-section),即基础图,对偶超图 H∗ 也有。这种结构叫做线图(line graph),它记录了所有超边的关联关系。线图在图论中被广泛使用,可以帮助我们分析图中的连接方式和复杂性。
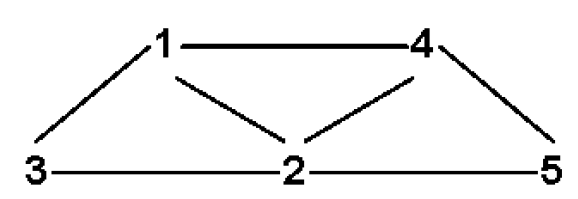
2. 边的交集有大小
在普通图中,所有边的大小都是2,也就是每条边只连接两个顶点。但在超图中,边的大小可以是任意数值,例如1、2或更多。边可能是单个顶点的集合,也可能是两个顶点或多个顶点的集合。
在一个图中,考虑两条边e={u,v}和f={w,z},它们的交集g=e∩f 如果不为空(即g≠∅),则这两条边是相交的(incident)。交集的大小s(e,f)=∣g∣表示交集中的顶点数。在图中,相交的边的交集通常只有一个顶点(s(e,f)=1),但在超图中,交集的大小可以是1到两个边的最小长度之间的任何数值。
3. 边可以嵌套
在图中,两条边要么相交,要么不相交。但在超图中,还有另一种情况:边可以嵌套(nested)或者包含(included)。如果边 e 是边 f 的子集,或 f 是 e 的子集,这就是边的嵌套性。边的交集大小s(e,f) 等于两条边中较小的一条边的大小。
4. 步行的长度和宽度
步行(walk)是指一系列相邻边的序列 W=⟨e0,e1,…,eN⟩,其中每对相邻边是相交的。步行的长度 N 是步行中边的数量。
步行的长度和宽度是图和超图的核心概念。在图中,步行的长度定义了顶点之间的连接方式,并且帮助我们在图中“走”过顶点之间的路径。在图中,步行的每对相邻边的交集大小si=1,也就是说步行总是1-步行。而在超图中,交集的大小si可能变化,因此步行的宽度s(W) 是步行中最小交集大小。如果步行的宽度是s,则称为s-步行。
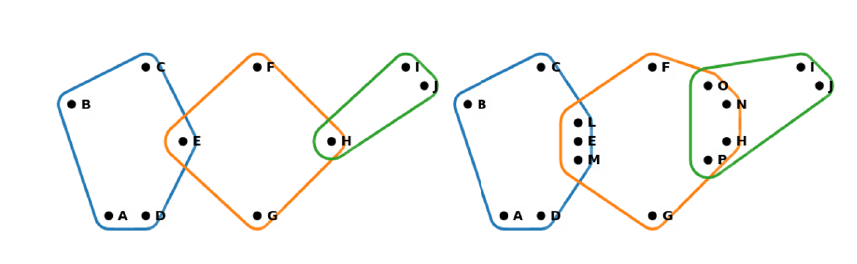
左侧的步行宽度为1,而右侧的步行宽度为3。
😱😱进阶的主题😱😱
1. s-步行(s-walks)与超网络(hypernetwork)科学
网络科学(Network Science)近年来已经成为数据分析中的一股重要力量,它用于衡量距离、连接性、可达性、中心性、模块化等属性的各种方法。这些方法可以通过引入超图中的“s-版本”来进行推广。
什么是 s-步行?
s-步行 是指在超图中两条边之间的最短路径,它的特点是需要更宽的连接。具体来说,两个顶点或超边之间的 s-距离 是它们之间最短 s-步行 的长度。当 s 增加时,这意味着需要更广泛的连接,因此距离也会增加。最终,随着 s 的增加,可能会出现一些顶点之间变得无法通过 s-步行 到达的情况。简而言之,s-步行 是分析超图中节点或边之间连接性的关键工具,它能够揭示网络中更深层次的关系,尤其是在连接要求变宽时的可达性变化。 s-步行 在超图中的广泛应用,表明它可以推广并扩展现有的网络科学概念,用于处理复杂的多维网络结构。
2. 超图与数学紧密联系
超图在数学中的广泛应用及其与其他重要数学结构的深层联系,尤其是在离散科学领域
①超图与二分图的关系
超图与二分图(bipartite graph)有着一对一的对应关系。超图H=(V,E)可以转换为一个二分图B=(V∪E,I),其中二分图的顶点集包含原超图中的顶点和超边。二分图中的每条边{v,e}∈I 表示原超图中顶点 v 位于超边 e 中。因此,我们可以根据任意一个二分图定义一个超图,但并非所有操作都能在二分图与超图之间相互转换。
下图👇展示一个二分图的例子,图中不同颜色的线连接了顶点和超边,表示它们之间的关系。
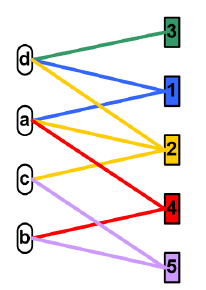
②布尔关联矩阵与超图的关系
超图的布尔关联矩阵I 也可以看作二元关系的特征矩阵。简化概念的超图中(即有限的、无环的、简单的、连通的,并且没有空的超边、孤立的顶点、标签、权重或属性),关联矩阵的使用会受到一些限制,但总体来说,超图、二元关系和二分图之间存在一对一的对应关系。
③超图的层次结构
每个超图都蕴含一个层次结构。具体来说,超边之间要么存在包含关系,要么它们的交集是相互包含的。这种结构创建了一个偏序(partial order),进一步映射到一系列格结构(lattice structures),这些结构描述了顶点和超边之间的包含关系。
下图👇展示了一个超图的概念格(concept lattice),这是超图中最重要的结构之一。概念格通过显示顶点和边的关系,帮助我们理解超图中元素之间的包含和关联。

理解这个图的关键是要明白它反映了不同元素(顶点和超边)之间的包含或嵌套关系。每一层之间的节点通过连接线相连,这些连接线表示顶点和超边之间的包含关系。例如,顶点“a”通过连接线连接到了超边“1”,表示“a”是超边“1”的一部分。
节点的含义:
灰色方框(如“1”、“2”、“3”、“4”、“5”):这些表示的是超边。每一个方框代表超图中的一条超边。
白色圆点:白色圆点代表了集合的不同组合,这些组合表示不同的顶点或超边的结合。
黑色和蓝色的半圆:黑色半圆和蓝色半圆代表的是不同的超边中所包含的顶点。
黑色半圆:黑色半圆代表了集合中顶点的组合,它们通常位于超边的底部。黑色半圆表示这些顶点已经被组合在一起形成了一个集合或超边。
蓝色半圆:蓝色半圆用于标记某些超边中包含的顶点。例如,超边“2”和“4”中都有蓝色的半圆,表示这些超边包含某些特定的顶点。
连接线的含义:
每一条从顶点(a、b、c、d)到超边(1、2、3、4、5)的连线表示包含关系。例如,如果顶点“a”与超边“1”有连接线,这意味着顶点“a”是超边“1”的一部分。
④超图与拓扑学的关系
超图的强大之处在于它能够建模多向交互。同样,拓扑学(topology)也关心多维对象如何相互连接,不仅限于连续空间,还包括离散对象。实际上,有限拓扑空间是超图的一种特殊形式,它在并和交运算下闭合,并与前面提到的格结构有深层次的联系。
⑤抽象单纯复形(ASC)
在这个背景下,抽象单纯复形(abstract simplicial complex, ASC)是一种超图,其中所有可能的包含边都存在。每个超图可以通过“闭合”操作形成这样的单纯复形。ASC 具有自然的拓扑结构,能够通过同调(homology)揭示隐藏的结构,并被广泛应用于拓扑方法,如持久同调(persistent homology)。
什么是抽象单纯复形(ASC)?
抽象单纯复形是超图的一种特殊形式,在该结构中,所有可能的子集都被包含。它是离散数学和拓扑学中常用的概念,用于研究集合之间的包含关系。抽象单纯复形包含的“单纯形”代表了不同维度的集合:
0维单纯形:单个顶点。
1维单纯形:由两顶点构成的边。
2维单纯形:由三个顶点构成的三角形(填充的面)。
更高维度的单纯形:由更多顶点构成的几何对象。
抽象单纯复形是一种更高维度的扩展,它不仅包含所有顶点,还包含顶点之间所有可能的组合边及其高维扩展。
下图👇展示了如何从一个超图生成一个抽象单纯复形。该图显示了原始超图中的超边及其包含的所有子边(包括单点边)。这些子边和超边共同构成了抽象单纯复形的完整结构。
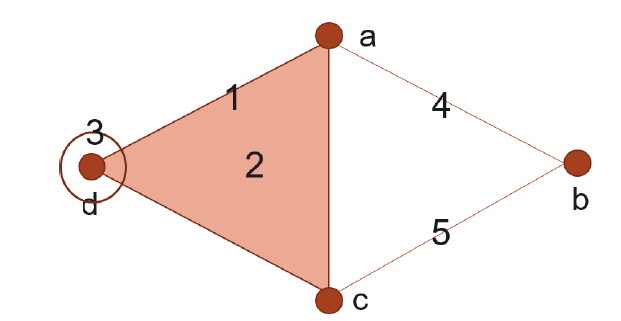
3. 更复杂的图和超图
之前简化图的定义——有限、无环、简单、连通,没有空超边、孤立顶点、标签、权重或属性。而在复杂图中,可以遇到更多种类的图或超图结构。比如以下这些情况的出现会让图和超图变得复杂:
1. 空超边(Empty Hyperedges)
如果关联矩阵III 中的某一列全部为零,这表示该超边是空的,也就是没有任何顶点与它关联。空超边在一些复杂的超图中是允许存在的。
2. 孤立顶点(Isolated Vertices)
如果关联矩阵III 中的某一行全部为零,这表示该顶点是孤立的,也就是该顶点没有连接到任何超边。孤立顶点通常表示在图或超图的某些结构中,某些顶点并不参与任何连接。
3. 多重超图(Multihypergraphs)
允许重复的超边,这意味着在关联矩阵中,可能会有重复的列(表示相同的超边重复出现)。这种结构在某些应用场景中是有意义的,尤其是在考虑复杂系统或网络中,某些连接可能重复发生。
4. 自环(Self-Loops)
自环表示图中的某条边可以连接到自己。在通常的图结构中,边通常是连接两个不同的顶点,而在允许自环的结构中,边可以连接到同一个顶点,这是一种特殊的连接方式。
5. 方向(Direction)
有些图中的边可以被赋予方向性,也就是边的连接有输入和输出的顶点。在这种情况下,某些顶点被视为“输入”,而另一些顶点则是“输出”。这种定向连接在网络模型中经常使用,比如表示信息流、交通流等。
6. 顺序(Order)
在某些超图中,顶点可能具有特定的顺序。这种顺序可能是全序或部分序。对于图而言,这相当于定向边的概念,但在超图中,顺序的复杂性更高,因为超边可以连接多个顶点。
7. 属性(Attributes)
一般来说,我们可以在图或超图的顶点、边或“关联关系”上附加属性。这些属性可以是不同的数据类型,例如权重、标签、标识符、类型、字符串等。具体来说,属性可以应用于:
-
顶点:关联矩阵的行,表示每个顶点的属性。
超边:关联矩阵的列,表示每条边或超边的属性。
关联关系(Incidences):关联矩阵的单元格,表示某个顶点出现在某个超边中的具体方式。这些属性能够让超图更加灵活地表示复杂的关系。
假设我们使用一个超图来表示一个复杂的社交网络:
空超边可能表示某个活动没有任何参与者。
孤立顶点可能表示某个用户没有参与任何活动。
多重超边可能表示多个活动有重复的参与者。
自环可能表示某个用户独自参与了某项活动。
方向性可能用于表示信息流动的方向,比如信息从某个人流向另一个人。
顺序可能用于表示某些活动需要特定顺序的参与者。
属性可以记录每个用户或每项活动的相关信息,如用户的年龄、活动的类型等。
最后
别再纠结什么2-均匀超图了
生活已经够复杂了
祝各位国庆节愉快
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








