数学建模笔记——TOPSIS[优劣解距离]法

TOPSIS(优劣解距离)法

1. 基本概念

C. L.Hwang和 K.Yoon于1981年首次提出 TOPSIS(Technique for Order Preference by Similarity to an Ideal Solution),可翻译为逼近理想解排序法,国内常简称为优劣解距离法。

TOPSIS法是一种常用的综合评价方法,能充分利用原始数据的信息,其结果能精确地反映各评价方案之间的差距。

TOPSIS法引入了两个基本概念:

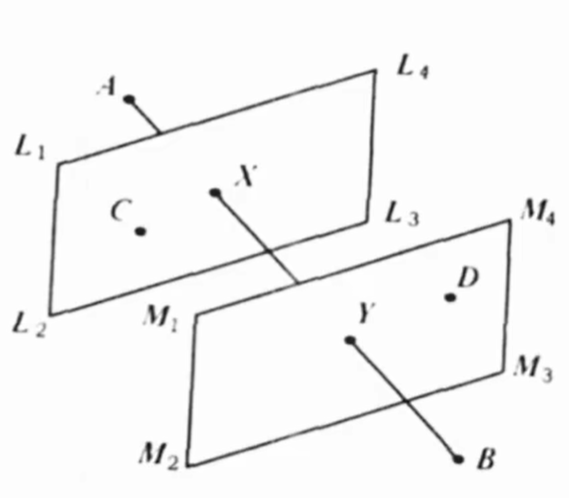
• 理想解:设想的最优的解(方案),它的各个属性值都达到各备选方案中的最好的值;
• 负理想解:设想的最劣的解(方案),它的各个属性值都达到各备选方案中的最坏的值。方案排序的规则是把各备选方案与理想解和负理想解做比较,若其中有一个方案最接近理想解,而同时又远离负理想解,则该方案是备选方案中最好的方案。TOPSIS通过最接近理想解且最远离负理想解来确定最优选择。

2. 模型原理

TOPSIS法是一种理想目标相似性的顺序选优技术,在多目标决策分析中是一种非常有效的方法。它通过归一化后(去量纲化)的数据规范化矩阵,找出多个目标中最优目标和最劣目标(分别用理归想一解化和反理想解表示),分别计算各评价目标与理想解和反理想解的距离,获得各目标与理想解的贴近度,按理想解贴近度的大小排序,以此作为评价目标优劣的依据。贴近度取值在0~1之间,该值愈接近1,表示相应的评价目标越接近最优水平;反之,该值愈接近0,表示评价目标越接近最劣水平。

3. 基本步骤

1. 将原始矩阵正向化

   将原始矩阵正向化，就是要将所有的指标类型统一转化为极大型指标

2. 将正向化矩阵标准化

   标准化的方法有很多种，其主要目的就是去除量纲的影响，保证不同评价指标在同一数量级，且数据大小排序不

3. 计算得分并归一化

   $S_i=\frac{D_i^{-}}{D_i^{+}+D_i^{-}}$,其中$S_i$为得分,$D_i^{+}$为评价对象与最大值的距离，$D_i^{-}$

为评价对象与最小值的距离。

4. 典型例题

明星Kun想找一个对象，但喜欢他的人太多，不知道怎么选，经过层层考察，留下三个候选人。他认为身高165是最好的，体重在90-100斤是最好的。

候选人	颜值	牌气(争吵次数)	身高	体重
A	9	10	175	120
B	8	7	164	80
C	6	3	157	90

4.1 矩阵正向化

常见的指标类型：

指标名称	指标特点	例子
极大型 (效益型) 指标	越大(多)越好	成绩、 GDP增速、 企业利润
极小型 (成本型) 指标	越小(少)越好	费用、 坏品率、污染程度
中间型指标	越接近某个值越好	水质量评估时的PH值
区间型指标	落在某个区间最好	体温、 水中植物性营养物量

在 TOPSIS 方法中，就是要将所有指标进行统一正向化，即统一转化为极大型指标。 那么就需要极小型、中间型以及区间型的指标进行转化为极大型指标。

指标名称	公式
极大型(效益型)指标	/
极小型(成本型)指标	$\tilde{x}=max-x$, $\tilde{x}$为指标值,$max$为指标最大值,$x$为指标值
中间型指标	{ x i } \{x_i\} {xi​} 是一组中间型序列，最优值是 $x_{best}$，$M = max{
区间型指标	$x_i$是一组区间型序列，最佳区间为$[a,b]$，正向化公式如下 M = m a x { a − m i n { x i } , m a x { x i } − b } , x ~ i = { 1 − a − x i M , x i < a 1 , a ≤ x i ≤ b 1 − x i − b M , x i > b M=max\{a-min\{x_i\}, max\{x_i\}-b\}, \widetilde{x}_i=\begin{cases}1-\frac{a-x_i}{M}, x_i<a\\1, a\leq x_i\leq b\\1-\frac{x_i-b}{M}, x_i>b\end{cases} M=max{a−min{xi​},max{xi​}−b},x i​=⎩ ⎨ ⎧​1−Ma−xi​​,xi​<a1,a≤xi​≤b1−Mxi​−b​,xi​>b​

1. 颜值为极大型指标

2. 脾气为极小型指标

   候选人	颜值	$max$	$max-x$
   A	10	10	0
   B	7	10	3
   C	3	10	7

3. 身高为中间型指标

   候选人	身高	$x_{best}$	|$x_i-x_{best}$|	${\hat{x}}_i$
   A	175	165	10	1
   B	164	165	1	1/10
   C	157	165	8	8/10

4. 体重为区间型指标

   候选人	体重	$M$	${\hat{x}}_i$
   A	120	20	0
   B	80	20	1/2
   C	90	20	1

正向化后的矩阵为

候选人	颜值	牌气(争吵次数)	身高	体重
A	9	0	0	0
B	8	3	0.9	0.5
C	6	7	0.2	1

4.2 正向矩阵标准化

标准化的目的是消除不同指标量纲的影响

假设有n个要评价的对象，m个评价指标（已经正向化了）构成的正向化矩阵如下：
$$X=\left[\begin{array}{cccc}{x}_{11}& x_{12}& \cdots & x_{1m}\\ x_{21}& x_{22}& \cdots & x_{2m}\\ ⋮& ⋮& \ddots & ⋮\\ x_{n1}& x_{n2}& \cdots & x_{nm}\end{array}\right]$$
那么对其标准化后的矩阵记为Z，Z的每一个元素：
$$z_{ij}=\frac{x_{ij}}{\sqrt{{\sum }_{i=1}^n{x}_{ij}^2}}$$
即（每一个元素/根号下所在列元素的平方和）得到标准化矩阵Z:
$$Z=\left[\begin{array}{cccc}{z}_{11}& z_{12}& \cdots & z_{1m}\\ z_{21}& z_{22}& \cdots & z_{2m}\\ ⋮& ⋮& \ddots & ⋮\\ z_{n1}& z_{n2}& \cdots & z_{nm}\end{array}\right]$$
标准化后，还需要给不同指标加上权重，采用的权重确定方法有层次分析法、熵权法、Delphi法、对数最小二乘法。这里认为各个指标权重相同。

对上述矩阵进行标准化，得

候选人	颜值	牌气(争吵次数)	身高	体重
A	0.669	0	0	0
B	0.595	0.394	0.976	0.447
C	0.446	0.919	0.217	0.894

4.3 计算得分并归一化

定义最大值：

Z + = ( m a x { z 11 , z 21 , ⋯   , z n 1 } , m a x { z 12 , z 22 , ⋯   , z n 2 } , ⋯   , m a x { z 1 m , z 2 m , ⋯   , z n m } ) Z^+=(max\{z_{11},z_{21},\cdots,z_{n1}\},max\{z_{12},z_{22},\cdots,z_{n2}\},\cdots,max\{z_{1m},z_{2m},\cdots,z_{nm}\}) Z+=(max{z11​,z21​,⋯,zn1​},max{z12​,z22​,⋯,zn2​},⋯,max{z1m​,z2m​,⋯,znm​})
定义最小值：
Z − = ( m i n { z 11 , z 21 , ⋯   , z n 1 } , m i n { z 12 , z 22 , ⋯   , z n 2 } , ⋯   , m i n { z 1 m , z 2 m , ⋯   , z n m } ) Z^-=(min\{z_{11},z_{21},\cdots,z_{n1}\},min\{z_{12},z_{22},\cdots,z_{n2}\},\cdots,min\{z_{1m},z_{2m},\cdots,z_{nm}\}) Z−=(min{z11​,z21​,⋯,zn1​},min{z12​,z22​,⋯,zn2​},⋯,min{z1m​,z2m​,⋯,znm​})
定义第i (i=1,2,…,n) 个评价对象与最大值的距离：
$$D_i^{+}=\sqrt{\sum _{j=1}^m(Z_j^{+}-z_{ij}{)}^2}$$
定义第i (i=1,2,…,n) 个评价对象与最小值的距离：
$$D_i^{-}=\sqrt{\sum _{j=1}^m(Z_j^{-}-z_{ij}{)}^2}$$
那么，我们可以计算得出第 i( i=1,2,…,n) 个评价对象未归一化的得分：
$$S_i=\frac{D_i^{-}}{D_i^{+}+D_i^{-}}$$

很明显 0≤Si≤1,且 Si 越大 Di+ 越小，即越接近最大值。

我们可以将得分归一化并换成百分制：
$$\widetilde{S_{\mathrm{i}}}=\frac{S_{\mathrm{i}}}{{\sum }_{i=1}^n{S}_{\mathrm{i}}}\times 100$$

4.4 python代码实现

import numpy as np

# 从用户输入参评数目和指标数目
print("请输入参评数目：")
n = int(input())
print("请输入指标数目：")
m = int(input())

# 接受用户输入的类型矩阵
print("请输入类型矩阵：1. 极大型 2. 极小型 3. 中间型 4.区间型")
kind = input().split(" ")

# 接受用户输入的矩阵并转化为向量
print("请输入矩阵：")
A = np.zeros(shape=(n, m))
for i in range(n):
    A[i] = input().split(" ")
    A[i] = list(map(float, A[i]))
print("输入矩阵为：\n{}".format(A))

# 极小型指标转化为极大型指标的函数


def minTomax(maxx, x):
    x = list(x)
    ans = [[(maxx-e) for e in x]]
    return np.array(ans)

# 中间型指标转化为极大型指标的函数


def midTomax(bestx, x):
    x = list(x)
    h = [abs(e-bestx) for e in x]
    M = max(h)
    if M == 0:
        M = 1  # 防止最大差值为0的情况
    ans = [[1-(e/M) for e in h]]
    return np.array(ans)

# 区间型指标转化为极大型指标的函数


def regTomax(lowx, highx, x):
    x = list(x)
    M = max(lowx-min(x), max(x)-highx)
    if M == 0:
        M = 1  # 防止最大差值为0的情况
    ans = []
    for i in range(len(x)):
        if x[i] < lowx:
            ans.append(1-(lowx-x[i])/M)
        elif x[i] > highx:
            ans.append(1-(x[i]-highx)/M)
        else:
            ans.append(1)
    return np.array([ans])


# 同一指标类型，将所有指标转化为极大型指标
X = np.zeros(shape=(n, 1))
for i in range(m):
    if kind[i] == "1":
        v = np.array(A[:, i])
    elif kind[i] == "2":
        maxA = max(A[:, i])
        v = minTomax(maxA, A[:, i])
    elif kind[i] == "3":
        print("类型三，请输入最优值：")
        bestA = eval(input())
        v = midTomax(bestA, A[:, i])
    elif kind[i] == "4":
        print("类型四，请输入区间[a,b]值a：")
        lowA = eval(input())
        print("类型四，请输入区间[a,b]值b：")
        highA = eval(input())
        v = regTomax(lowA, highA, A[:, i])
    if i == 0:
        X = v.reshape(-1, 1)  # 如果是第一个指标，直接赋值
    else:
        X = np.hstack((X, v.reshape(-1, 1)))  # 如果不是第一个指标，横向拼接
print("统一指标后矩阵为：\n{}".format(X))

# 对统一指标后的矩阵进行标准化处理
X = X.astype(float)  # 将X转化为浮点型
for i in range(m):
    X[:, i] = X[:, i]/np.sqrt(sum(X[:, i]**2))  # 对每一列进行归一化处理，即除以该列的欧几里得范数
print("标准化后矩阵为：\n{}".format(X))

# 最大值和最小值距离的计算
x_max = np.max(X, axis=0)  # 计算每一列的最大值
x_min = np.min(X, axis=0)  # 计算每一列的最小值
# 计算每一个参评对象与最优情况的距离d+
d_z = np.sqrt(np.sum(np.square(X-np.tile(x_max, (n, 1))), axis=1))
# 计算每一个参评对象与最差情况的距离d-
d_f = np.sqrt(np.sum(np.square(X-np.tile(x_min, (n, 1))), axis=1))
print("每个指标的最大值为：{}".format(x_max))
print("每个指标的最小值为：{}".format(x_min))

# 计算每一个参评对象的综合得分
s = d_f/(d_f+d_z)  # 根据d+和d-计算每一个参评对象的得分，其中s接近1表示越好，接近0表示越差
Score = 100*s/sum(s)  # 将得分转换为百分制
for i in range(n):
    print(f"第{i+1}个参评对象的得分为：{Score[i]}")

输入：

请输入参评数目：
3
请输入指标数目：
4
请输入类型矩阵：1. 极大型 2. 极小型 3. 中间型 4.区间型
1 2 3 4
请输入矩阵：
9 10 175 120
8 7 164 80
6 3 157 90
输入矩阵为：
[[  9.  10. 175. 120.]
 [  8.   7. 164.  80.]
 [  6.   3. 157.  90.]]
类型三，请输入最优值：
165
类型四，请输入区间[a,b]值a：
90
类型四，请输入区间[a,b]值b：
100

输出:

统一指标后矩阵为：
[[9.  0.  0.  0. ]
 [8.  3.  0.9 0.5]
 [6.  7.  0.2 1. ]]
标准化后矩阵为：
[[0.66896473 0.         0.         0.        ]
 [0.59463532 0.3939193  0.97618706 0.4472136 ]
 [0.44597649 0.91914503 0.21693046 0.89442719]]
每个指标的最大值为：[0.66896473 0.91914503 0.97618706 0.89442719]
每个指标的最小值为：[0.44597649 0.         0.         0.        ]
第1个参评对象的得分为：8.886366735657832
第2个参评对象的得分为：45.653341055701134
第3个参评对象的得分为：45.46029220864103