矩阵谱半径

矩阵谱半径指的是矩阵的最大特征值（含绝对值）。

它可以判断收敛性，也可以判断方程解的稳定性。

一般情况下，当存在一个单位矩阵减去另外一个矩阵的形式时， 谱半径小于一就是为了确保它们之间的差值为正这样逆矩阵才会存在，可以用来验证一个方案是否可行。

The radius 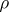 of the smallest closed disc in the plane that contains the spectrum of this element (cf. Spectrum of an element). The spectral radius of an element  is connected with the norms of its powers by the formula

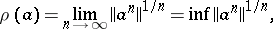which, in particular, implies that 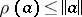 . The spectral radius of a bounded linear operator on a Banach space is the spectral radius of it regarded as an element of the Banach algebra of all operators. In a Hilbert space, the spectral radius of an operator is equal to the greatest lower bound of the norms of the operators similar to it (see [2]):

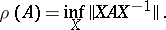If the operator is normal, then 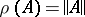 (cf. Normal operator).

 

 

定义：

Let λ₁, ..., λ_n be the (real or