前言
前面的学习中,笔者就二叉树、二叉查找树、平衡二叉树进行了一些总结。此篇文章主要
讨论伸展树。我们知道的是在二叉查找树上的基本操作(查找、插入)的时间复杂读与树的高度
成正比的关系。对于一个含有N个结点的二叉查找树来说,这些操作的最坏运行情况为OlogN)。
但是我们这知道在极端的情况下,会导致树退化为一个单支树,这导致了操作时间为O(N)。
为了克服上面的情况,出现了一些二叉查找树的变形,例如上篇文章的AVL树。以及接下来
要讨论的伸展树。
伸展树定义
伸展树是基于二叉查找树的,它不保证树一直是平衡的,但是各种操作的平均复杂读是
O(logN) 。
伸展树的设计是具体考虑到了局部性原理 (刚被访问的内容下次可能还被访问,查找次数
多的内容可能下次还被访问),为了使整个的查询时间更小,查询频率高的那些结点应当处于
靠近树根的位置。
这样,一个比较好的解决方案就是:每次查找就结点之后对树进行重新构造。把查找的结
点搬移到树根的位置,以这种方式自调整形式的二叉查找树就是伸展树。
旋转操作
搞清楚了伸展树的定义,那么我们来看看是如何实现结点的搬移操作的,和AVL树一样同样
是通过旋转来操作的。具体如何旋转,我们分三种情况。单旋转、一字旋转和之字旋转。
这里我们假定访问的结点为A
单旋转
对于单旋转操作,我们先看一个实例,之后对其略做分析。
此时,访问的结点A的父结点B是根结点,如果A是B的左孩子,我们对A、B直接进行一次
右旋转操作,同理如果结点A是B的右孩子则进行一次左旋转。具体操作就不给实例图了。
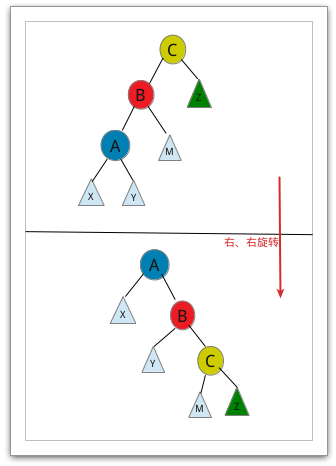
一字型旋转(左左、右右)
同样的我们先看一个实例操作图:
此时访问的是根结点,它是其父结点的左子树、且其父结点同时是也是左子树的情况下
我们需要进行右、右旋转来达到目地。至于A、B都是右子树的情况就不演示了,其操作为
左、左旋转。
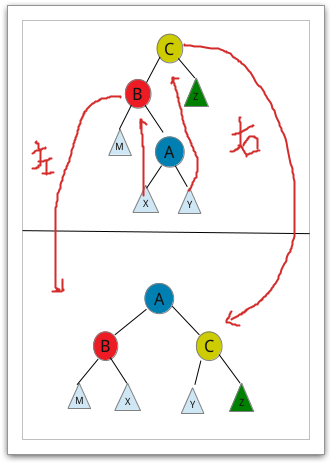
之字旋转
话不多说,我们首先看一个实际操作。
可以看出的是此时的情况与2有些相似,只是A、B所与的左右不一致了,对于其操作也不
详述了,图中的操作情况以给出。
伸展树实现(源码)
package com.kiritor;
/**伸展树
* @author Kiritor*/
public class SplayTree {
static class BinaryNode {
// Constructors
BinaryNode(Comparable theElement) {
this(theElement, null, null);
}
BinaryNode(Comparable theElement, BinaryNode lt, BinaryNode rt) {
element = theElement;
left = lt;
right = rt;
}
Comparable element;
BinaryNode left;
BinaryNode right;
}
private BinaryNode root;
private static BinaryNode nullNode;
static
{
nullNode = new BinaryNode(null);
nullNode.left = nullNode.right = nullNode;
}
private static BinaryNode newNode = null; //用于插入的操作
private static BinaryNode header = new BinaryNode(null);//用于调整操作
public SplayTree() {
root = nullNode;
}
public void insert(Comparable x) {
if (newNode == null)
newNode = new BinaryNode(x);//新建一个结点
//根结点为空则新建的结点作为根结点
if (root == nullNode) {
newNode.left = newNode.right = nullNode;
root = newNode;
} else {
root = splay(x, root);//调整
if (x.compareTo(root.element) < 0) {
newNode.left = root.left;
newNode.right = root;
root.left = nullNode;
root = newNode;
} else if (x.compareTo(root.element) > 0) {
newNode.right = root.right;
newNode.left = root;
root.right = nullNode;
root = newNode;
} else
return;
}
newNode = null;
}
public void remove(Comparable x) {
BinaryNode newTree;
root = splay(x, root);
if (root.element.compareTo(x) != 0)
return; // Item not found; do nothing
if (root.left == nullNode)
newTree = root.right;
else {
newTree = root.left;
newTree = splay(x, newTree);
newTree.right = root.right;
}
root = newTree;
}
public Comparable findMin() {
if (isEmpty())
return null;
BinaryNode ptr = root;
while (ptr.left != nullNode)
ptr = ptr.left;
root = splay(ptr.element, root);
return ptr.element;
}
public Comparable findMax() {
if (isEmpty())
return null;
BinaryNode ptr = root;
while (ptr.right != nullNode)
ptr = ptr.right;
root = splay(ptr.element, root);
return ptr.element;
}
public Comparable find(Comparable x) {
root = splay(x, root);
if (root.element.compareTo(x) != 0)
return null;
return root.element;
}
public void makeEmpty() {
root = nullNode;
}
public boolean isEmpty() {
return root == nullNode;
}
public void printTree() {
if (isEmpty())
System.out.print("Empty tree ");
else
printTree(root);
}
private BinaryNode splay(Comparable x, BinaryNode t) {
BinaryNode leftTreeMax, rightTreeMin;
header.left = header.right = nullNode;
leftTreeMax = rightTreeMin = header;
nullNode.element = x;
for (;;)
if (x.compareTo(t.element) < 0) {
if (x.compareTo(t.left.element) < 0)
t = rotateWithLeftChild(t);
if (t.left == nullNode)
break;
rightTreeMin.left = t;
rightTreeMin = t;
t = t.left;
} else if (x.compareTo(t.element) > 0) {
if (x.compareTo(t.right.element) > 0)
t = rotateWithRightChild(t);
if (t.right == nullNode)
break;
// Link Left
leftTreeMax.right = t;
leftTreeMax = t;
t = t.right;
} else
break;
leftTreeMax.right = t.left;
rightTreeMin.left = t.right;
t.left = header.right;
t.right = header.left;
return t;
}
static BinaryNode rotateWithLeftChild(BinaryNode k2) {
BinaryNode k1 = k2.left;
k2.left = k1.right;
k1.right = k2;
return k1;
}
static BinaryNode rotateWithRightChild(BinaryNode k1) {
BinaryNode k2 = k1.right;
k1.right = k2.left;
k2.left = k1;
return k2;
}
private void printTree(BinaryNode t) {
if (t != t.left) {
printTree(t.left);
System.out.print(t.element.toString()+" ");
printTree(t.right);
}
}
public static void main(String[] args) {
SplayTree tree = new SplayTree();
tree.insert(12);
tree.insert(8);
tree.insert(2);
tree.insert(4);
tree.insert(14);
tree.insert(16);
tree.insert(6);
tree.insert(1);
tree.insert(11);
tree.remove(8);
System.out.println("被查找的节点:" + tree.find(11));
System.out.println("此时的根:" + tree.root.element);
System.out.println("被查找的节点:" + tree.find(12));
System.out.println("此时的根:" + tree.root.element);
System.out.println("被查找的节点:" + tree.find(11));
System.out.println("此时的根:" + tree.root.element);
System.out.println("伸展树值情况:");
tree.printTree();
}
}
运行情况为:


























 1057
1057

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








