小波概念理解

Daubechies小波

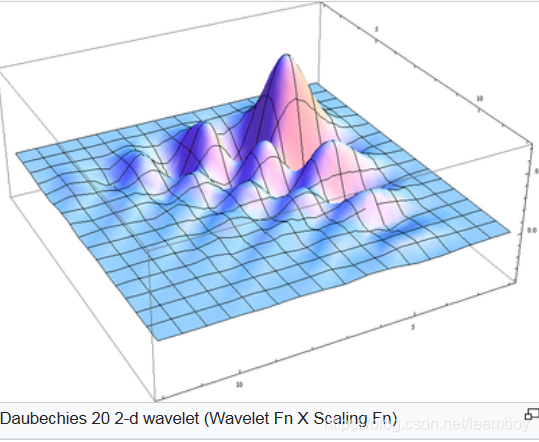
支撑长度
        小波函数Ψ(t)、Ψ(ω)、尺度函数φ(t)和φ(ω)的支撑区间，是当时间或频率趋向于无穷大时，Ψ(t)、Ψ(ω)、φ(t)和φ(ω)从一个有限值收敛到0的长度。支撑长度越长，一般需要耗费更多的计算时间，且产生更多高幅值的小波系数。大部分应用选择支撑长度为5~9之间的小波，因为支撑长度太长会产生边界问题，支撑长度太短消失矩太低，不利于信号能量的集中。
        这里常常见到“紧支撑”的概念，通俗来讲，对于函数f(x)，如果自变量x在0附近的取值范围内，f(x)能取到值；而在此之外，f(x)取值为0，那么这个函数f(x)就是紧支撑函数，而这个0附近的取值范围就叫做紧支撑集。总结为一句话就是“除在一个很小的区域外，函数为零，即函数有速降性”。
 

消失矩（Vanishing Moment）
        在实际中，对基本小波往往不仅要求满足容许条件，对还要施加所谓的消失矩（Vanishing Moments）条件，使尽量多的小波系数为零或者产生尽量少的非零小波系数，这样有利于数据压缩和消除噪声。消失矩越大，就使更多的小波系数为零。但在一般情况下，消失矩越高，支撑长度也越长。所以在支撑长度和消失矩上，我们必须要折衷处理。
        小波的消失矩的定义为，若

其中，Ψ(t)为基本小波，0<=p<N。则称小波函数具有N阶消失矩。从上式还可以得出，同任意n-1阶多项式正交。在频域内表示就是Ψ(ω)在ω=0处有高阶零点（一阶零点就是容许条件）。
正则性
        在量化或者舍入小波系数时，为了减小重构误差对人眼的影响，我们必须尽量增大小波的光滑性或者连续可微性。因为人眼对“不规则”(irregular)误差比“平滑”误差更加敏感。换句话说，我们需要强加“正则性”(regularity)条件。也就是说正则性好的小波，能在信号或图像的重构中获得较好的平滑效果，减小量化或舍入误差的视觉影响。但在一般情况下，正则性好，支撑长度就长，计算时间也就越大。因此正则性和支撑长度上，我们也要有所权衡。
        消失矩和正则性之间有很大关系，对很多重要的小波（比如，样条小波，Daubechies小波等）来说，随着消失矩的增加，小波的正则性变大，但是，并不能说随着小波消失矩的增加，小波的正则性一定增加，有的反而变小。

对于Daubechies小波

       一般来说，对于给定的支持宽度2A-1，Daubechies小波被选择为具有最高数目的消失矩A（这并不意味着最佳平滑度）。在使用中有两种命名方案，DN使用抽头的长度或数量，dbA使用消失矩的数量。因此，D4和DB2是相同的小波变换。

      在矩和正交性条件下的代数方程的2A_1可能解中，选择具有极值相位的尺度滤波器。小波变换也易于应用于快速小波变换。Daubechies小波在解决信号自相似性、分形问题、信号不连续性等问题中得到了广泛的应用。

      Daubechies小波不是根据得到的缩放和小波函数定义的，事实上，它们不可能以封闭形式写下来。下面的图是使用级联算法生成的，这是一种由简单的逆变换[1 0 0 0.…适当的次数。

scaling and wavelet functions 尺度与小波函数
above functions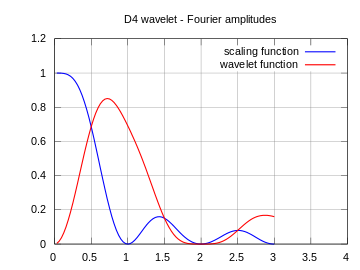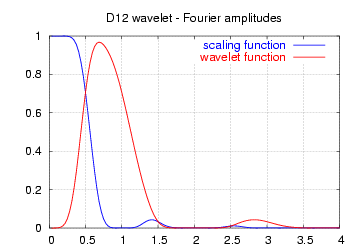

注意，这里所示的频谱不是高通和低通滤波器的频率响应，而是标度(蓝色)函数和小波(红色)函数的连续傅里叶变换的幅度。

 Daubechies正交小波D2-D20通常使用的是D1-DB10。索引数是指系数n的数目。每个小波都具有等于系数的一半的零矩或消失矩的数目。例如，D2（Haar小波）有一个消失矩，D4有两个消失矩，等等。消失矩限制了小波在信号中表示多项式行为或信息的能力。例如，具有一个消失矩的D2容易编码一个系数的多项式，或恒定的信号分量。D4编码具有两个系数的多项式，即常数和线性信号分量；D6编码3个多项式，即常数、线性和二次信号分量。然而，这种编码信号的能力受到在应用变换期间由离散移位操作(下文)引起的尺度泄漏现象和移位不变性的缺乏的影响。表示线性、二次(例如)信号分量的子序列根据点与序列中的偶数或奇数位置对齐的不同，通过变换进行不同处理。由于缺乏平移不变性的重要性质，导致了平移不变性（离散）小波变换的几个不同版本的发展。

构造

缩放序列(低通滤波器)和小波序列(带通滤波器)(参见正交小波以了解这种方式构造的细节)在这里将被归一化为和等于2和平方和等于2。在一些应用中，它们被标准化为和。因此，两个序列和它们的所有移位由偶数的系数彼此正交。利用逼近阶A的正交离散小波变换的尺度序列的一般表示

The scaling sequences of lowest approximation order

Below are the coefficients for the scaling functions for D2-20. The wavelet coefficients are derived by reversing the order of the scaling function coefficients and then reversing the sign of every second one, (i.e., D4 wavelet = {-0.1830127, -0.3169873, 1.1830127, -0.6830127}). Mathematically, this looks like b k = ( − 1 ) k a N − 1 − k {\displaystyle b_{k}=(-1)^{k}a_{N-1-k}} where k is the coefficient index, b is a coefficient of the wavelet sequence and a a coefficient of the scaling sequence. N is the wavelet index, i.e., 2 for D2.

Orthogonal Daubechies coefficients (normalized to have sum 2)

D2 (Haar)	D4	D6	D8	D10	D12	D14	D16	D18	D20
1	0.6830127	0.47046721	0.32580343	0.22641898	0.15774243	0.11009943	0.07695562	0.05385035	0.03771716
1	1.1830127	1.14111692	1.01094572	0.85394354	0.69950381	0.56079128	0.44246725	0.34483430	0.26612218
	0.3169873	0.650365	0.89220014	1.02432694	1.06226376	1.03114849	0.95548615	0.85534906	0.74557507
	-0.1830127	-0.19093442	-0.03957503	0.19576696	0.44583132	0.66437248	0.82781653	0.92954571	0.97362811
		-0.12083221	-0.26450717	-0.34265671	-0.31998660	-0.20351382	-0.02238574	0.18836955	0.39763774
		0.0498175	0.0436163	-0.04560113	-0.18351806	-0.31683501	-0.40165863	-0.41475176	-0.35333620
			0.0465036	0.10970265	0.13788809	0.1008467	6.68194092e-4	-0.13695355	-0.27710988
			-0.01498699	-0.00882680	0.03892321	0.11400345	0.18207636	0.21006834	0.18012745
				-0.01779187	-0.04466375	-0.05378245	-0.02456390	0.043452675	0.13160299
				4.71742793e-3	7.83251152e-4	-0.02343994	-0.06235021	-0.09564726	-0.10096657
					6.75606236e-3	0.01774979	0.01977216	3.54892813e-4	-0.04165925
					-1.52353381e-3	6.07514995e-4	0.01236884	0.03162417	0.04696981
						-2.54790472e-3	-6.88771926e-3	-6.67962023e-3	5.10043697e-3
						5.00226853e-4	-5.54004549e-4	-6.05496058e-3	-0.01517900
							9.55229711e-4	2.61296728e-3	1.97332536e-3
							-1.66137261e-4	3.25814671e-4	2.81768659e-3
								-3.56329759e-4	-9.69947840e-4
								5.5645514e-5	-1.64709006e-4
									1.32354367e-4
									-1.875841e-5

Parts of the construction are also used to derive the biorthogonal Cohen-Daubechies-Feauveau wavelets (CDFs).

Implementation

While software such as Mathematica supports Daubechies wavelets directly[2] a basic implementation is simple in MATLAB (in this case, Daubechies 4). This implementation uses periodization to handle the problem of finite length signals. Other, more sophisticated methods are available, but often it is not necessary to use these as it only affects the very ends of the transformed signal. The periodization is accomplished in the forward transform directly in MATLAB vector notation, and the inverse transform by using the circshift() function:

Transform, D4

It is assumed that S, a column vector with an even number of elements, has been pre-defined as the signal to be analyzed. Note that the D4 coefficients are [1+sqrt(3), 3+sqrt(3), 3-sqrt(3), 1-sqrt(3)]/4.

N = length(S);
s1 = S(1:2:N-1) + sqrt(3)*S(2:2:N);
d1 = S(2:2:N) - sqrt(3)/4*s1 - (sqrt(3)-2)/4*[s1(N/2); s1(1:N/2-1)];
s2 = s1 - [d1(2:N/2); d1(1)];
s = (sqrt(3)-1)/sqrt(2) * s2;
d = -(sqrt(3)+1)/sqrt(2) * d1;

Inverse transform, D4

d1 = d * ((sqrt(3)-1)/sqrt(2));
s2 = s * ((sqrt(3)+1)/sqrt(2));
s1 = s2 + circshift(d1,-1);
S(2:2:N) = d1 + sqrt(3)/4*s1 + (sqrt(3)-2)/4*circshift(s1,1);
S(1:2:N-1) = s1 - sqrt(3)*S(2:2:N);