1、三角形 如果三边是a,b,c
那么 c^2=a^2+b^2-2abcosc
海伦公式 求面积 半周长p=(a+b+c)/2
三角形面积 sqrt(p(p-a)(p-b)(p-c))
点积:x1x2+y1y2 |A||B|cosa
叉积:x1y2-x2y1 = S/2 |A||B|sina
注意用叉积求到的面积是有方向的!!
练习题目 http://cstest.scu.edu.cn/soj/problem.action?id=4249
2 欧拉函数
定义:对于正整数n,φ(n)是小于或等于n的正整数中,与n互质的数的数目。
例如:φ(8) = 4,因为1,3,5,7均和8互质。
性质:1.若p是质数,φ(p) = p-1.
2.若n是质数p的k次幂,φ(n) = (p-1)*p^(k-1)。因为除了p的倍数都与n互质
3.欧拉函数是积性函数,若m,n互质,φ(mn) = φ(m)φ(n).
根据这3条性质我们就可以推出一个整数的欧拉函数的公式。因为一个数总可以写成一些质数的乘积的形式。
E(k) = (p1-1)(p2-1)...(pi-1)*(p1^(a1-1))(p2^(a2-1))...(pi^(ai-1))
= k*(p1-1)(p2-1)...(pi-1)/(p1*p2*...*pi)
= k*(1-1/p1)*(1-1/p2)...(1-1/pk)
在程序中利用欧拉函数如下性质,可以快速求出欧拉函数的值(a为N的质因素)
若 ( N%a == 0 && (N/a)%a == 0 ) 则有:E(N) = E(N/a)*a;
若 ( N%a == 0 && (N/a)%a != 0 ) 则有:E(N) = E(N/a)*(a-1);
练习题目:http://acm.hdu.edu.cn/showproblem.php?pid=2824
欧拉定理:欧拉定理(也称费马-欧拉定理)是一个关于同余的性质。欧拉定理表明,若n,a为正整数,且n,a互质,(a,n) = 1,则a^φ(n) ≡ 1 (mod n)。
3.二次剩余
在数论中,特别在同余理论裏,一个整数  对另一个整数
对另一个整数  的二次剩余(英语:Quadratic residue)指
的二次剩余(英语:Quadratic residue)指  的平方
的平方  除以
除以  得到的余数。
得到的余数。
当对于某个 及某个
及某个 ,式子
,式子  成立时,称“
成立时,称“ 是模
是模 的二次剩余”
的二次剩余”
当对于某个 及某个
及某个 ,
, 不成立时,称“
不成立时,称“ 是模
是模 的二次非剩余”
的二次非剩余”
若 是奇质数且
是奇质数且 不能整除
不能整除 ,则:
,则:
-
 是模
是模
 的二次剩余
当且仅当:
的二次剩余
当且仅当:
-
 是模
是模
 的非二次剩余当且仅当:
的非二次剩余当且仅当:
以勒让德符号表示,即为: 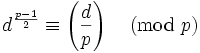
4.组合数

恒等式:若表示在n个物品中选取m个物品,则如存在下述公式: C(n,m)= C(n,n-m)= C(n-1,m-1)+C(n-1,m)








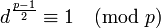
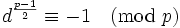














 1357
1357

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








