1. 广度优先算法的原理
1.1. 广度优先遍历基本思想
- 广度优先遍历(Board First Search)类似于分层搜索.
- 广度优先遍历需要使用一个队列以保存访问过的结点的顺序,
以便按照这个顺序来访问这些结点的邻接结点.
1.2. 广度优先遍历算法步骤
-
访问初始节点 V 并标记结点 V 为已访问
-
结点 V 入队列.
-
当队列非空时, 继续执行, 否则算法结束.
-
队列第一个结点出队, 取得队头结点 U.
-
查找结点 U 的第一个邻接结点 W.
-
若结点 U 的邻接结点 W 不存在, 则跳转到步骤 3;
否则执行以下三个步骤:- 若结点 W 未被访问, 则访问结点 W 并标记为已访问, 结点 W 入队列;
若结点 W 已被访问, 直接执行下一步. - 查找结点 U 的继 W 邻接结点后的下一个邻接结点 W;
- 跳转到步骤 6 进行循环执行直到跳出.
- 若结点 W 未被访问, 则访问结点 W 并标记为已访问, 结点 W 入队列;
1.3. 广度优先遍历案例分析
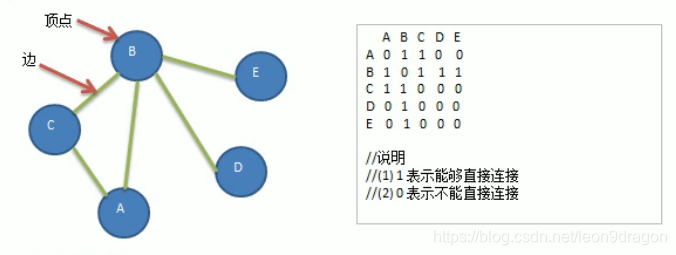
- 首先设置初始结点为 A, 结点 A 进入了队列, 输出: A
- 队列中的第一个结点出队, 即结点 A 出列, 并以结点 A 访问其邻接结点
- 访问 A 的第一个邻接结点 B, 发现能够连通, B 进入队列, 输出: A-B
- 访问 A 的下一个邻接结点 C, 发现能够联通, C 进入队列, 输出 A-B-C
- 访问 A 的下一个邻接结点 D, 发现不能联通, 则返回队列.
- 此时队列中第一个结点是结点 B, 因此结点 B 出列, 并以结点 B 来查找其邻接结点
- 访问 B 的邻接结点, A-C 都已经被访问过则继续查询直到出现或没有邻接结点为止
- 访问 B 的下一个邻接结点 D, 发现能够联通, D 进入队列, 输出 A-B-C-D
- 访问 B 的下一个邻接结点 E, 发现能够联通, E 进入队列, 输出 A-B-C-D-E
- 至此, 所有结点均被遍历输出, 遍历结束.
2. 广度优先算法的代码实现
- 均在图的基础代码上进行修改
2.1. 图的邻接矩阵类
package com.leo9.dc30.graph;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;
public class GraphMatrix {
//定义一个 ArrayList 用来存储图中的顶点的数据集合
private ArrayList<String> graph_vertex_list;
//定义一个二维数组存储图对应的邻接矩阵
private int[][] graph_edge_arr;
//定义变量存储图中的边的数目
private int edge_num;
//定义数组来记录某个结点是否已被访问
private boolean[] isVisited;
//region 构造器, 参数是顶点数量
public GraphMatrix(int vertex_num) {
//初始化邻接矩阵和顶点集合, 边的数目
//如果顶点有n个, 邻接矩阵就是n*n的矩阵
graph_edge_arr = new int[vertex_num][vertex_num];
//定义顶点集合的容量, 和顶点数量一致
graph_vertex_list = new ArrayList<String>(vertex_num);
//因为一开始并不知道有多少条边, 初始化的时候为0即可(这一步不写也可以)
edge_num = 0;
}
//endregion
//region 定义添加结点方法, 参数是结点对应的字符串
public void insertVertex(String vertex_str) {
//直接添加到集合即可
graph_vertex_list.add(vertex_str);
}
//endregion
//region 定义添加边的方法
/**
* @param vertex1 结点1在集合中的编号, 即顶点在集合中的下标[0~n]
* @param vertex2 结点2在集合中的编号, 即顶点在集合中的下标[0~n]
* @param edge_weight 两个结点之间边的权值, 默认为 0 不连通, 大于 0 就连通
*/
public void insertEdge(int vertex1, int vertex2, int edge_weight) {
//因为是无向图. 因此顶点间的两个方向的边都要进行定义
graph_edge_arr[vertex1][vertex2] = edge_weight;
graph_edge_arr[vertex2][vertex1] = edge_weight;
//边产生之后, 边的数目自增
edge_num++;
}
//endregion
//region 图中常用的方法
//region 返回结点的个数
public int getVertexNum() {
//直接返回顶点集合的size即可
return graph_vertex_list.size();
}
//endregion
//region 返回边的数目
public int getEdgeNum() {
//直接返回边的数目即可
return edge_num;
}
//endregion
//region 返回结点下标对应的结点数据, 例如 0 号结点对应结点数据为 "A"
public String getValByIndex(int vertex_index) {
return graph_vertex_list.get(vertex_index);
}
//endregion
//region 返回vertex1和vertex2构成的边的权值
public int getEdgeWeight(int vertex1, int vertex2) {
//直接返回二维数组的对应下标成员即可
return graph_edge_arr[vertex1][vertex2];
}
//endregion
//region 显示图所对应的邻接矩阵
public void showGraphMatrix() {
for (int[] link : graph_edge_arr) {
System.out.println(Arrays.toString(link));
}
}
//endregion
//endregion
//region 遍历中用到的通用方法
//region 获取目标结点的第一个邻接结点的下标
/**
* @param target 目标结点的下标
* @return 遍历邻接矩阵找出与目标结点构成边的第一个结点,
* 有则返回第一个邻接结点下标;
* 没有则返回 -1.
*/
public int getFirstNeighbour(int target) {
for (int i = 0; i < graph_vertex_list.size(); i++) {
if (graph_edge_arr[target][i] > 0) {
return i;
}
}
return -1;
}
//endregion
//region 根据目标结点的前一个邻接结点的下标获取下一个邻接结点的下标
/**
* @param target 目标结点
* @param pre_neighbour 目标结点的上一个邻接结点的下标
* @return 若存在下一个邻接结点, 则返回其下标, 否则返回 -1
*/
public int getNextNeighbour(int target, int pre_neighbour) {
for (int i = pre_neighbour + 1; i < graph_vertex_list.size(); i++) {
if (graph_edge_arr[target][i] > 0) {
return i;
}
}
return -1;
}
//endregion
//endregion
//region 深度优先遍历的相关方法
//region 深度优先遍历, 第一部分
//对一个结点进行深度优先遍历
private void searchByDepthFirst(boolean[] isVisited, int init_vertex) {
//先访问第一个结点, 并输出
System.out.printf("[%s] -> ", getValByIndex(init_vertex));
//将结点设置成已访问状态
isVisited[init_vertex] = true;
//获取初始结点的第一个邻接结点
int the_neighbour = getFirstNeighbour(init_vertex);
//判断这个邻接结点是否存在, 存在则开始循环
while (the_neighbour != -1) {
//如果这个结点没被访问过, 则递归遍历
if (!isVisited[the_neighbour]) {
searchByDepthFirst(isVisited, the_neighbour);
}
//如果这个节点已经访问过, 则寻找下一个邻接结点, 并替换当前邻接结点的下标
else {
the_neighbour = getNextNeighbour(init_vertex, the_neighbour);
}
}
}
//endregion
//region 深度优先遍历, 第二部分
//重载第一部分的方法, 用作当邻接结点不存在时的递归策略
//遍历所有的结点, 进行深度优先遍历, 默认初始结点为 0 号结点
public void searchByDepthFirst() {
//定义记录数组的容量
isVisited = new boolean[graph_vertex_list.size()];
for (int i = 0; i < getVertexNum(); i++) {
if (!isVisited[i]) {
searchByDepthFirst(isVisited, i);
}
}
}
//endregion
//endregion
//region 广度优先遍历相关方法
//region 广度优先遍历, 第一部分
//对一个节点进行广度优先遍历
private void searchByBoardFirst(boolean[] isVisited, int init_vertex) {
//定义变量用以存放队列第一个结点的下标
int first_in_queue;
//定义变量用以存放邻接结点的下标
int neighbour_vertex;
//定义队列用以存储结点访问顺序
LinkedList queue = new LinkedList();
//输出访问结果
System.out.printf("[%s] -> ", getValByIndex(init_vertex));
//将结点标记为已访问
isVisited[init_vertex] = true;
//将结点加入队列尾部
queue.addLast(init_vertex);
//当队列不为空, 则开始循环出队找邻接结点
while (!queue.isEmpty()) {
//取出队列中第一个结点
first_in_queue = (Integer) queue.removeFirst();
//取出队列中第一个结点的第一个邻接结点下标
neighbour_vertex = getFirstNeighbour(first_in_queue);
//当邻接结点存在时
while (neighbour_vertex != -1) {
//如果邻接结点没有被访问过, 已被访问则跳过
if (!isVisited[neighbour_vertex]) {
//输出这个邻接结点, 将其标记已访问并将其放入队列
System.out.printf("[%s] -> ", getValByIndex(neighbour_vertex));
isVisited[neighbour_vertex] = true;
queue.addLast(neighbour_vertex);
}
//继续查找下一个邻接结点, 并替换当前邻接结点的下标
neighbour_vertex = getNextNeighbour(first_in_queue, neighbour_vertex);
}
}
}
//endregion
//region 广度优先遍历, 第二部分
//对所有结点都进行广度优先遍历
public void searchByBoardFirst(){
//定义记录数组的容量
isVisited = new boolean[graph_vertex_list.size()];
for (int i = 0; i < getVertexNum(); i++) {
if (!isVisited[i]) {
searchByBoardFirst(isVisited, i);
}
}
}
//endregion
//endregion
}
2.2. 测试类
package com.leo9.dc30.graph;
public class TestGraphMatrix {
public static void main(String[] args) {
//结点个数
int vertex_num = 5;
//用字符串数组存放结点值
String[] VertexVal = {"A", "B", "C", "D", "E"};
//创建图对象
GraphMatrix graph_matrix = new GraphMatrix(vertex_num);
//循环添加顶点
for(String vertex_val: VertexVal){
graph_matrix.insertVertex(vertex_val);
}
//添加边, 因为是无向图, 添加一次即可
//A-B A-C B-C B-D B-E
graph_matrix.insertEdge(0,1,1);
graph_matrix.insertEdge(0,2,1);
graph_matrix.insertEdge(1,2,1);
graph_matrix.insertEdge(1,3,1);
graph_matrix.insertEdge(1,4,1);
//列印邻接矩阵
System.out.println("===================");
graph_matrix.showGraphMatrix();
//深度优先遍历
//System.out.println("===================");
//graph_matrix.searchByDepthFirst();
//广度优先遍历
System.out.println("===================");
graph_matrix.searchByBoardFirst();
}
}
2.3. 测试结果
- 如下图输出结果所示, 成功将所有的结点都遍历了一次.
6647
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
