容性阻抗不连续对信号完整性影响-CSDN博客

本文链接：https://blog.csdn.net/lhprjj/article/details/136504394

文章详细分析了容性阻抗不连续点对反射系数的影响，以RC电路为例，探讨了电容充电过程中的阻抗变化和反射现象。它指出，容性负载的反射系数随时间变化，对信号传输产生时变影响，特别是在总线系统中可能导致时序问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1. 背景

容性阻抗与电阻阻抗的反射式有区别的，对于电阻性阻抗不连续点，两侧的阻抗值恒定，从而反射系数也是恒定。但是对于容性阻抗不连续点，两侧阻抗不恒定且随时间变化的，因此反射系数也是岁时间变化的。

2. 分析

2.1 RC电路

如下图RC电路，根据大学电路分析知识，我们假设高电平幅度为A=1V，驱动源电阻R=50Ω，负载电容C=10pF，则电容两端电压可以表示为

$V_{c}=A(1-e^{-\frac{t}{\tau}})$

其中 $\tau$ =RC为电路时间常数，当电容充电时间 $t= \tau$ 时，电容两端电压为

$V_{c}=A(1-e^{-1})=63.2\%\cdot A$

以上公式表明，当充电时间经历 $\tau$ 时，电容电压值上升到最终值得63.2%。

根据电容电流公式可以得出电流：

$I_{c}=C\frac{dV_{c}}{dt}=\frac{A}{R}e^{-\frac{t}{\tau}}$

因此，电容阻抗可表示为

$Z_{c}=\frac{V_{c}}{I_{c}}=R(e^{\frac{t}{\tau}}-1)$

将R=50Ω，C=10pF带入上式，激励源为上升边为0的阶跃信号，电容两端电压和电流变化曲线如下图所示。当t= $\tau$ =RC=500ps时，电容电压上升到632mV，是高电平的63.2%。

电容的阻抗曲线如下图所示，电压刚加到电容的瞬间，电容的阻抗为0，随着电容充电，阻抗逐渐增大，随着时间增加，阻抗变为无穷大，最终相当于开路。

从阻抗Zc表达式推算，当t= $\tau \cdot ln2$ =347ps时，电容阻抗等于源阻抗R=50Ω，与上图电容的阻抗曲线mark结果一致。 $\tau =RC$ 越大，电容阻抗变化越缓慢。

2.2 末端容性负载的反射

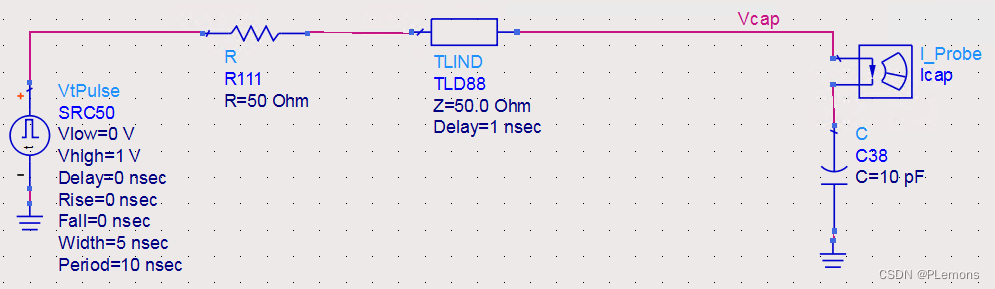
传输线末端的接收器都存在输入电容，焊盘，封装等都有一定的寄生电容。输入寄生电容有几pF到十几pF。此输入电容对信号来说就是一个阻抗不连续点，这个输入电容在末端就是一个容性负载，因此末端就会产生反射。

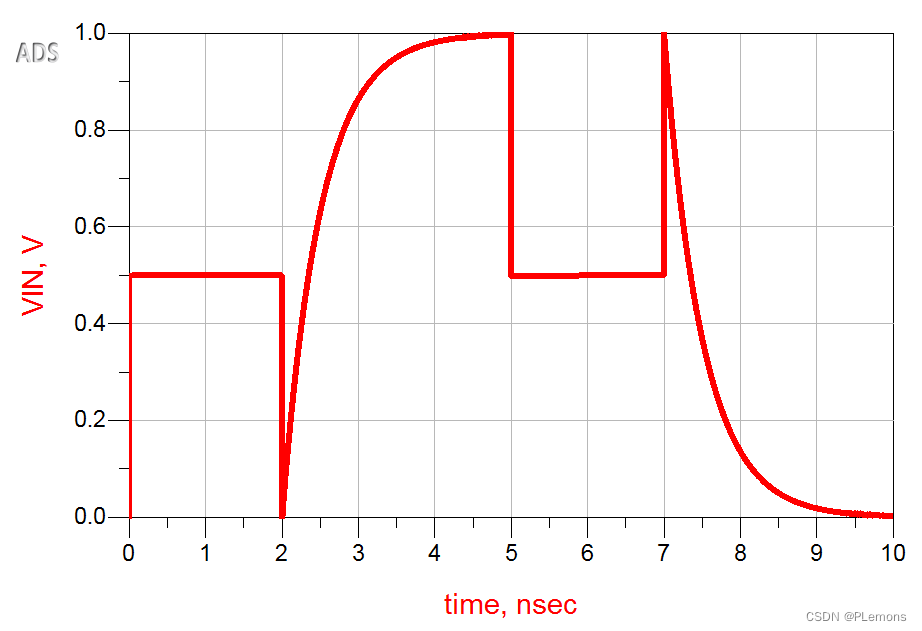
如下图所示，假设激励信号上升时间为0，输出阻抗50Ω，传输线延迟为1ns，末端电容为10pF。理想方波幅度为1V，当方波经过1ns传输延时的传输线后达到末端电容，瞬间电容会有一个很大的电流，随着电容的充电，电压逐渐增大，电流逐渐减小。经过500ps之后电容电压达到632mV，正好是高电平的63.2%。与计算 $\tau =Z_{0}C=50\cdot 10ps=500ps$ 很吻合。

电容的阻抗为

$Z_{c}=\frac{V_{c}}{I_{c}}={Z_{0}}(e^{\frac{t}{\tau}}-1)$

电容阻抗曲线如下图所示，经过t= $\tau\cdot ln2$ =50x100xln2=347ps后的电容阻抗大于传输线阻抗50Ω。

对于容性负载来说，阻抗是时变的，反射系数也是时变的。反射系数可以使用如下公式表示：

$\Gamma =\frac{Z_{c}-Z_{0}}{Z_{c}+Z_{0}}=\frac{Z_{0}(e^{\frac{t}{\tau }}-1)-Z_{0}}{Z_{0}(e^{\frac{t}{\tau }}-1)+Z_{0}}=1-2\cdot e^{-\frac{t}{\tau }}$

1> t=1ns时，电容阻抗为0Ω，相当于短路，反射系数 $\Gamma =-1$ ；

2> t=0.7 $\tau$ 时，电容阻抗为50Ω，电容阻抗等于传输线阻抗，反射系数 $\Gamma =0$

3> t= $\propto$ 时，电容阻抗为无穷大，相当于开路，反射系数 $\Gamma =1$ ；

如下图所示，发射端波形和接收端波形。在发射端，2ns后末端反射回来的信号回到发送端，入射和反射的波形叠加电压降到0，随着时间增加，电压按照指数增加，上升时间由时间常数 $\tau =Z_{0}C$ 决定。若是入射信号是理想方波信号，那么指数规律的上升沿与电容充电时间两端电压变化一致，在下降沿时，会产生一个与信号跳变方向相反的脉冲波形。若在传输线发送端附近有其他的接收器，那么向下的尖峰会非常危险。