线性回归-小白篇（高级篇是详细解释）

1.1问题来源：找出自变量X1 ，X2，X3，Xm与因变量Y之间的函数关系。例如：房子面积X1与房子位置X2，房子房间数目X3与房子价格的关系式子：

高中：Y（房子价格）=aX（房子面积）+b
有两组（X=1，Y=8），（X=2，Y=13）求出a=5,b=3。就知道Y=5X+3

大学：因为X(价格)，S（面积），Q（房子外观）等等一堆变量，就得引入Xn表示X，S，Q。。。等等。用Wn表示a,b等等。

然后简化成向量的形式

wT我们通常习惯用
wT
wTwTW向量表示则是theta与上面式子Wm一样：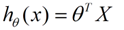

当然了有人用theta表示：线性回归的hypothesis表示为：

最终求得W就能够找出关系函数了，那不是多元函数求解？？？

好啦，这是高中的思维，其实很难求解的，理由是（小文字看看无妨，不看也罢）：

这个就是一个组合问题，已知一些数据，如何求里面的未知参数，给出一个最优解。 一个线性矩阵方程，直接求解，很可能无法直接求解。有唯一解的数据集，微乎其微。

基本上都是解不存在的超定方程组。因此，需要退一步，将参数求解问题，转化为求最小误差问题，求出一个最接近的解，这就是一个松弛求解。

求一个最接近解，直观上，就能想到，误差最小的表达形式。仍然是一个含未知参数的线性模型，一堆观测数据，其模型与数据的误差最小的形式，模型与数据差的平方和最小：

既然难以求解就找一个拟合公式，大概表示一下。
w T1.2 判断拟合效果或者预测效果好不好就有公式（ Least square作为loss function）：

高中：

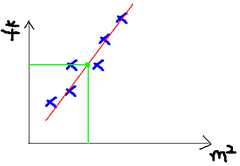
公式的意思是：我找出关系式然后和i组实际数据比较差值最小的即使最好拟合的。高中的最小二乘法y=ax+b

高中：红色是我们求出的函数y(x),蓝色是实际的蓝色点（y实际）,是不是红色与红色差值越小效果越好呢？

可是大学：多了好多变量，好多维。。。

大学：表示的公式复杂了：

i是第i组数据：(机器学习里面的第i组训练数据)

输入编号i	平方英尺X1	价格X2
1	150	6450
2	200	7450
3	250	8450
4	300	9450
5	350	11450
6	400	15450
7	600	18450

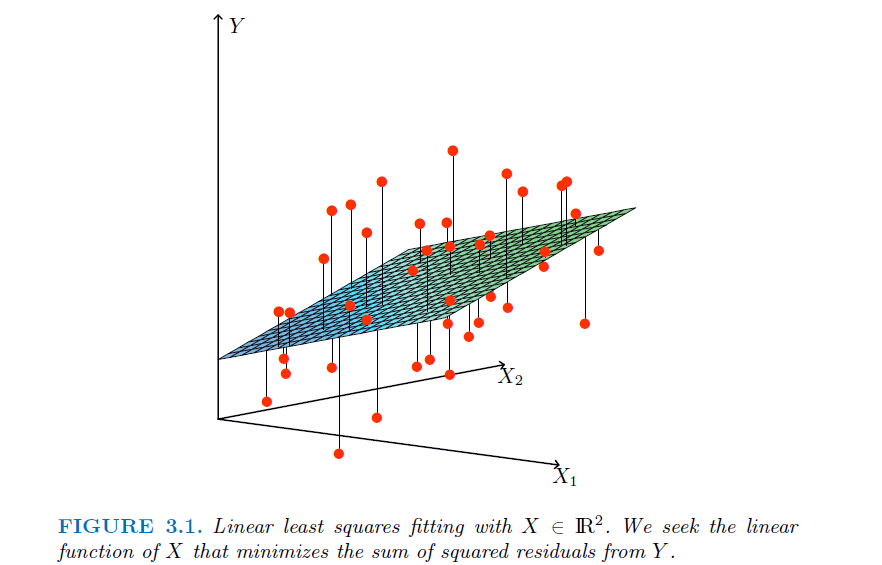
引用来自：http://www.tuicool.com/articles/MRbee2i

其实不管前面多少维，多少不了解，我们就是要找一条拟合最好的函数式子

我们还是想高中一样求最小的差值，而差值与谁关系最大呢？就是theta，式子就是下面（记住背也要背住）：

学习的目标是求loss function最小时的解θ* ，

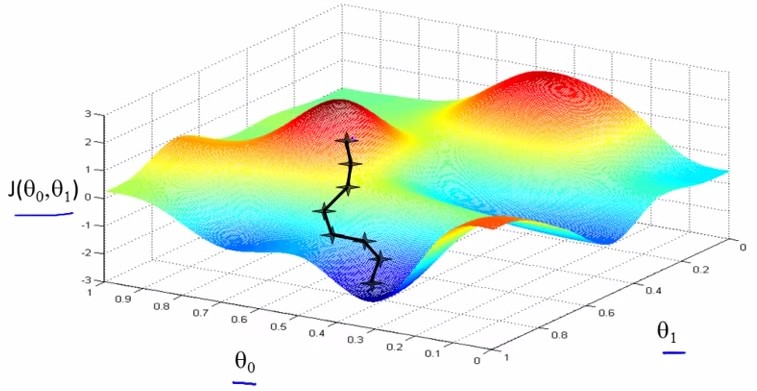
而求出theta文章就结束了，公式已经知道了，图如下：

注意此部分不同前面的已知多组(X，Y)(X,Y)(X,Y)求theta。现在的X是theta ,Y是J（theta），求最小的min(J(tehta))。

求出差值最小的点不就OK？大学与高中求最小值不是求导然后函数等于0,就是最小值。

3 Gradient 梯度求最小值

所谓梯度就是变化最快的方向（求导）：

高中：求导就是求斜率，找出函数的斜率

（下面是引用别人文章http://blog.csdn.net/jzlxiaohei/article/details/8973410）

大学：多维就是一座山，但是斜率有好多个，这时你就得在山上环顾四周找斜率最大的，最大的斜率越大越陡峭，下落越快

二维情况：斜率的方向是由θ₀和θ₁共同确定的。沿θ₀方向走一定长度，沿θ₁方向走一定长度，两个向量相加，就确定了要下降的方向，即确定两个向量的长度比例即可。

实际上，这个方向是梯度的负方向(为什么是负呢，因为求导是增长最快的方向，相差个负)。梯度方向，是函数上升最快的方向，那么负梯度方向当然就是下降最快的方向。关于梯度的推导和性质，可以参考高等数学的相关内容(记得是同济版高数书下册的空间几何相关章节，不确定)。这里直接给出其形式：

 

J对θ₀求偏导，得到沿θ₀方向前进的距离；J对θ₁求偏导，得到沿θ₁方向前进的距离；保持两个向量的比例，即确定了下一步的前进方向。

对于h=a* x + b的情况，假设这一步需要沿a方向走d(a)距离，沿b方向走的d(b)距离，那么在一次迭代中，只要下式同步更新a和b的值，那么这次迭代后，J函数就沿下降最快的方向，走了一步

a := a + α * d(a)

 b: = b +α* d(b)

对于步长α，总的来说就是不能太大，也不要太少。有没有一种自然辨证法的感觉（⊙﹏⊙|汗）。想象一个二次曲线，如果步子太大，会直接把最低点夸过去，而且步子大了，还有可能扯着那啥；步子太小，收敛太慢。步长一般不是常数，是一个函数，就是说随着迭代的进行，它的值会变化。

迭代公式的思想其实很简单，就是：

下一个值 =当前值 +步长 *方向

这个式子可以高度概括最优化这门课一半以上的内容，有这个式子，这门课就可以及格了~ ~。

总的来说就是，找每个维的比例确定最快的方向=theta这一步-下降最好的方向theta的斜率。那么a,b两个方向什么时候结束？

上一次的a与这次的a相差不大就可以了，这就是你在山下了，山下的最低点有个特点越来越平缓，斜率越来越小，就就是说你走前一步与后一步是差不多的。这样你就可以结束了。

上面是一维的图。

对于线性回归问题，多维梯度下降的公式变为（右边复杂的公式就是多维的斜率下降最快的方向也就是求导）：

需要注意的是，参数θ0,θ1...θ2在每一轮的迭代中是同步更新的。也就是说，在某一轮更新中，任意参数的更新值，不会参与其他参数的更新计算中。

最后一次次代入i组数值theta一维=theta一维-a步长（一维的第一组数据：房子面积X theta1+房子位置Xtheta2...减去y的实际值；第二组；第三组）好复杂的公司，编程的计算量蛮大的。但是能够求解，同时，由于线性回归的loss function是一个凸函数，所以用梯度下降法可以得到唯一的全局最优解。

请看第二章：快速梯度计算。。。。。。。。。。。

w T

w T