矩形覆盖问题

问题描述：
我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？
解法一：
设 2*n 的大矩形有F(n)种被覆盖方法。
1）当n = 0时，大矩形为空，显然F(0) = 0；
2）当n = 1时，大矩形与小矩形规格相同，F(1) = 1；
3）当n = 2时，使用2个小矩形可覆盖大矩形，但横竖摆放各有1种方法，故F(2) = 2；
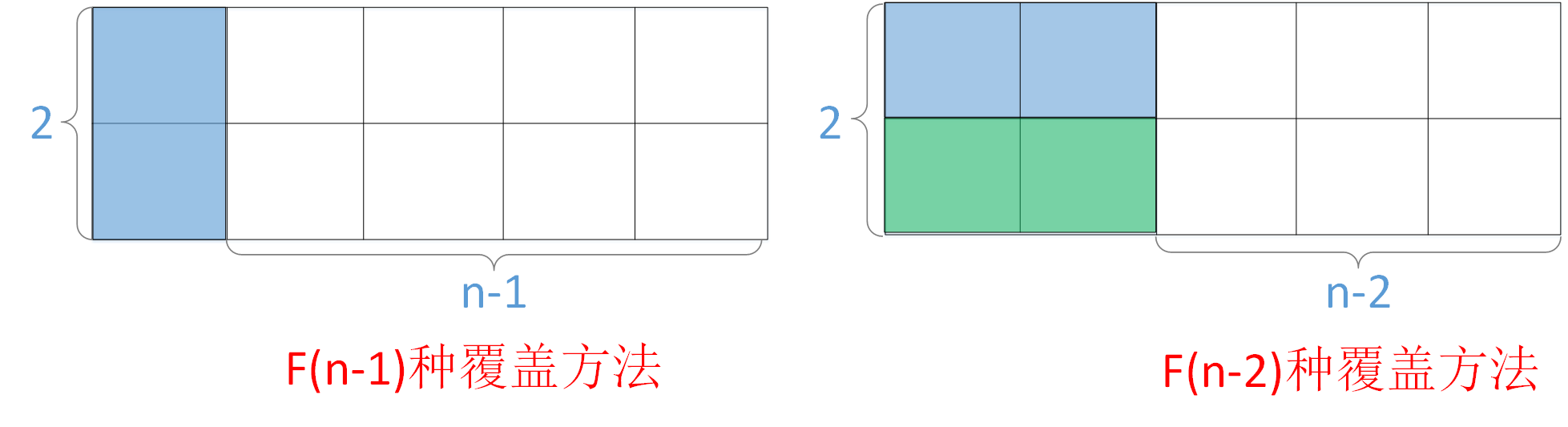
4）当n > 2时，覆盖方法可分为两大类（见下图）：1.先用 2*1 的小矩形覆盖大矩形的第一列，其后 n-1 列则有 F(n - 1)种覆盖方法；2.先用两个 2*1 的小矩形覆盖大矩形的前两列，其后 n-2 列共有F(n - 2)种覆盖方法， 故有递推公式 F(n) = F(n - 1) + F(n - 2)。
由此可见，An = F(n) 跟数学上的斐波拉契数列类似(不同点：严格定义的斐波拉契数列F(2) = F(0) + F(1) = 1)，求F(n)也就是求类斐波拉契数列的第n项的值。

落实到代码上，有2种实现方法：1)迭代实现，2)递归实现。
迭代实现：

  /** 用迭代方法计算斐波拉契数列 */
  public int RectCover(int n) {
    if (n <= 2) 
      return n;

    int index = 3;    // 从第3项开始需要递推计算F(n)
    int value1 = 1;   // F(n - 2)
    int value2 = 2;   // F(n - 1)
    do {
      int tmp = value2;
      value2 = value1 + value2;   // 计算F(n) = F(n - 2) + F(n - 1)
      value1 = tmp;
      index++;
    }
    while (index <= n); 

    return value2; 
  }

递归实现：

  /** 递归实现 */
  public int RectCover(int n) {
    if (n <= 2)  // 递归终止条件
      return n;

    int count = RectCover(n - 1) + RectCover(n - 2);
    return count;
  }

该实现时间复杂度较高，因为存在重复计算问题。举例来说，为了计算F(5)，由于F(5) = F(4) + F(3), 程序需要递归计算F(4)和F(3)。而F(3) = F(2) + F(1), F(4) = F(3) + F(2), 为了计算F(3)和F(4), 程序需要递归计算F(2)各一次，也就是是说F(2)被重复计算了。当n的规模越大，F(m)，m < n 被重复计算的次数会越多。
为了解决重复计算问题，可以将递归中间计算结果F(m)暂存在散列表中，此后递归若再次遇到F(m)，则从散列表中将计算结果直接取出即可，不再进行递归。
代码如下：

import java.util.*;

public class Solution {

  Map<Integer, Integer> map = new HashMap<Integer, Integer>();
  /** 递归实现 */
  public int RectCover(int n) {
    if (n <= 2)  // 递归终止条件
      return n;

    int res = 0;
    // 散列表未存有计算结果，递归计算并存入散列表
    if (!map.containsKey(n)) {    
      res = RectCover(n- 1) + RectCover(n- 2);
      map.put(n, res);        
    // 散列表存有计算结果，从散列表中取出          
    } else {                        
      res = map.get(n);  
    }
    return res;
  }
}

解法二：
转化成排列组合问题。如图所示，当大矩形被小矩形完全覆盖后，大矩形内存在2种类型的区块：1、由1个竖向小矩形组成的小块，称为“A块”；2.由2个横向小矩形组合而成的大块，称为”B块”。

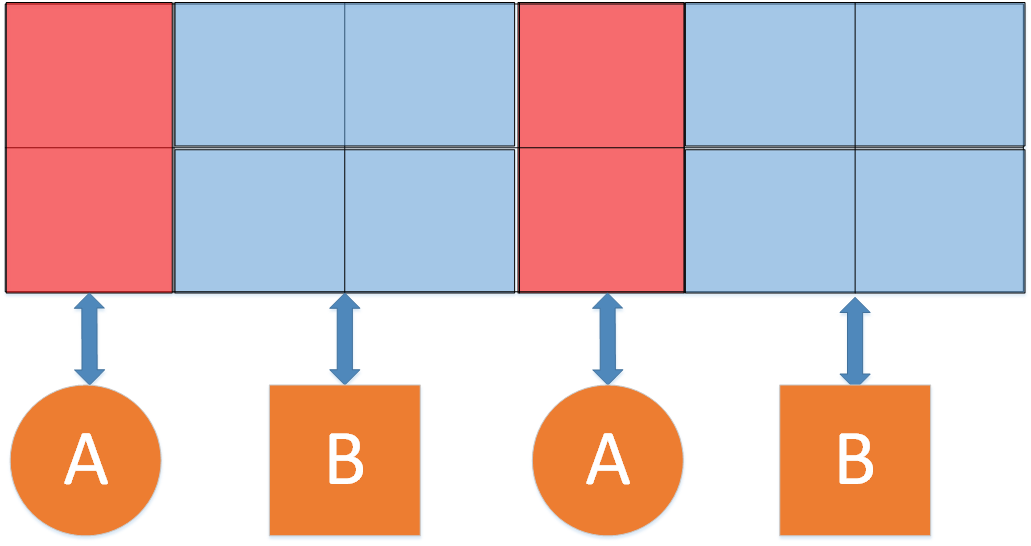
大矩形的“A块”和“B块”可以有不同数量组合(减少1个”B块”会相应地增加2个“A块”)和多种排列方式。大矩形的“A块”和”B块”的不同的数量划分情况下不同的排列方式，均对应不同的矩形覆盖方法。因此，问题可被转换为排列组合问题，矩形覆盖方法数等于“A块”、“B块”所有数量划分情形下的所有排列方式数量之和。
具体实现见代码：

public int RectCover(int n) {
    if (n <= 0)
      return 0; // 特殊情形

    int n1 = n / 2; // “B块”最大个数
    int n2 = n % 2; // “A块”最少个数

    int result = 0;
    /**
    * 每次减少1个“B块”，相应增加2个“A块”，并计算排列种数
    */ 
    for (int i = n1; i >= 0; i--) { 
      int sum = i + n2 + (n1 - i) * 2; // 块总数
      result += comb(sum, i);
    }

    return result;
  }

  // 计算组合数
  private int comb(int m, int n) {
    n = n < (m - n) ? n : (m - n);
    int res = 1;
    for (int i = 1; i <= n; i++)
      // 这个用到了组合数的性质c(8,4)=8/1*7/2*6/3*5/4=c(8,3)*5/4
      res = res * m-- / i; 
    return res;
  }