数学-e的自然之美

目录：

一、前言

二、利息中的e

1、e如何被发现

2、e的流行定义

3、e的通俗解释

4、利息的逆运算

三、对数发明的历史

四、微积分中的e

五、自然界中的对数螺线

六、C代码输出斐波那契数列

---

一、前言

现代我们知道，没有受过基础数学教育的人要想理解这些数，不仅需要了解更复杂的概念模型，还要熟悉加、减、乘、除等运算方法，只有这样才能完全明白。而更复杂的数，例如无理数、代数数和超越数，也需要了解更复杂的运算。形如下面的式子，竟然-1与e^(iπ)存在着如此的关系，是不是很神奇！？

推导过程：数学的精美之4、欧拉公式推导★

今天我们的主角就是这个超越数e，既然理解e的含义需要理解相关的运算，而这些运算最早都和利息有关。

二、利息中的e

1、e如何被发现

常数e是一个数学中非常重要的常数，它与自然对数的底数相同，约为2.71828。它最初由数学家约翰·纳皮尔在研究复利时发现，可以表示连续复利的极限情况。

随后，欧拉在研究无穷级数时又发现了e的重要性，称之为“自然对数的底数”，因为它在求对数时出现得特别频繁，具有一些非常有用的性质。

2、e的流行定义

图片来自：Common Definitions of e (Colorized)

其中，Max compounded growth下面的“3、e的通俗解释”有详细的描述，Infinite Series见微积分基础-微分篇之“8、泰勒Taylor公式及其应用”，Inverse of ln(x)推导如下：

3、e的通俗解释

e和圆周率π都是超越数，π的含义可以通过下图的割圆术来很形象的理解。π(C = πd→π = C/d)是所有圆共享的周长和直径之间的比率，它是所有圆固有的基本比率；e是所有持续增长过程共享的基本增长率。

假设等边形的对角线长为1，只要等边形的边足够多，算出来的周长就可以越来越接近圆周率π。

但是解释e的含义却很难找到这样直观的例子，阮一峰翻译的文章《数学常数e的含义》说的很好。

某种类的一群单细胞生物每24小时全部分裂一次。在不考虑死亡与变异等情况下，那么很显然，这群单细胞生物的总数量每天都会增加一倍。据此我们可以写出它的增量公式：growth = 2x(x表示天数)。

这个式子可以改写成：growth = (1+100%)*x 其中，1表示原有数量，100%表示单位时间内（24小时）的增长率。

根据细胞生物学，每过12个小时，也就是分裂进行到一半的时候，平均会新产生一半原数量的新细胞，新产生的细胞在之后的12小时内已经在分裂了。

因此一天24个小时可以分成两个阶段，每一个阶段的细胞数量都在前一个阶段的基础上增长50%，列出数学表达式：

亦即：

即在一个单位时间内，这些细胞的数量一共可以增至为原数量的2.25倍。

倘若这种细胞每过8小时就可以产生平均1/3的新细胞，新生细胞立即具备独立分裂的能力，那就可以将1天分成3个阶段，在一天内时间细胞的总数会增至：

即最后细胞数扩大为原数量的2.37倍。

实际上，这种分裂现象是不间断、连续的，每分每秒产生的新细胞，都会立即和母体一样继续分裂，一个单位时间（24小时）最多可以得到多少个细胞呢？答案是：

当增长率为100%保持不变时，在单位时间内细胞种群最多只能扩大2.71828倍。数学家把这个数就称为e，它的含义是单位时间内，持续的翻倍增长所能达到的极限值。

所以e的数学表达式如下图，来源于：An Intuitive Guide To Exponential Functions & e。

有了这个值以后，计算银行的复利就非常容易。

假定有一家银行，每年的复利是100%，请问存入100元，一年后可以拿多少钱？

答案是：

但是事实上，存储利息没有这么高，如果复利率只有5%，那么100元存一年可以拿到多少钱呢：

我们知道，在100%利率的情况下，n = 1000时，下式的值非常接近e：

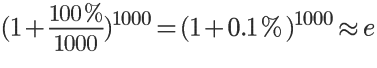
为了便于思考，取n = 50：

当利率是5%时，存款增长率就相当于e的20分之一次方：

1/20正好等于5%，所以我们可以把上式改写成：

rate表示利率。

再考虑时间因素，如果存款年限t年，那么存款最终增长率为：

这说明e可以用于任何连续不断的复合式增长率的计算，而上式也是这个增长率的通用计算公式。

带着这个结论再回到上面的例子。如果银行的利率是5%的复利，求解100元存款翻倍需要多少时间就等价于解下面的方程：

计算结果得13.86年，即：

可以看出：用72除以增长率就是翻倍的大致时间，这正是著名的72定律。

在原文《An Intuitive Guide To Exponential Functions & e》中找到了e的更直观的图，只要理解了这个例子，e的含义也就明白了。

假设你在银行存了1元钱（下图蓝圆），很不幸同时又发生了严重的通货膨胀，银行存款利率达到了逆天的100%！

银行一般1年才付一次利息，根据下图，满1年后银行付给你1元利息（绿圆），存款余额 = 2元

银行发善心，每半年付利息，你可以把利息提前存入，利息生利息(红圆)，1年存款余额 = 2.25元。

假设银行超级实在，每4个月就付利息，利息生利息（下图红圆、紫圆），年底的余额 ≈ 2.37元。

假设银行人品爆发，一年365天，愿意天天付利息，这样利滚利的余额 ≈ 2.71456748202元。

假设银行丧心病狂的每秒付利息，你也丧心病狂的每秒都再存入，1年共31536000秒，利滚利的余额 ≈ 2.7182817813元。

这个数越来越接近于e了！哎呀！费了半天劲也没多挣几个钱啊！

对！1元存1年，在年利率100%下，无论怎么利滚利，其余额总有一个无法突破的天花板，这个天花板就是e，有兴趣可以用这个网上计算器算一下。

类似的规律，在自然界中随处可见，也不止动物生长的细胞分裂、利息计算，植物生长、人口的增长、放射性衰变等也一样，所以就叫自然底数了。

我们和圆周率再做个对比：

• 多边形的边数和利滚利的次数是相似的。
• 对角线为1的n边等边形，n趋于无穷，周长就无限接近于π，即π是周长的最大值。
• 年利率为1（100%）的1元存款，利滚利的次数n趋于无穷，存款就无限接近e，即e是存款的最大值。

换种表述方法：

• 每个完美的圆，其周长都是π的倍数；
• 每个理想的存款，其余额都是e的倍数。

这里停一停，你好好体会一下。

按照自然的观点，如果圆是最美的，那最赚钱也是最理想的。

有人问了：为啥银行不每秒返利息呢？这样就不是100%回报率，而是171.8%了，还我的71.8%！

银行哭到：臣妾做不到啊！！！以上是意淫，银行不会这样发利息，洗洗睡吧。

4、利息的逆运算

还是从一个虚构的故事开始：

• 有一土豪要去银行存入大额存款，比如存1元。
• 银行经理推荐他投资理财产品，因为年利率高达100%，按照指数运算，bla bla bla……
• 但土豪的数学只有小学水平，听不懂有点烦，就问投资多长时间才能到10倍，100倍，1000倍？
• 经理有点懵，土豪不按常理出牌啊！
• 一般人都是根据存款时间问收益，例如收益第1年多少、第2年多少、第3年多少……
• 土豪居然逆向思维，根据收益问时间，多少年2倍，多少年5倍，多少年10倍！
• 不愧是老板，不问过程，只问结果！
• 于是经理就从第1年开始算，把10年内每年的收益都算出来，列成一个收益列表，如下图：

  

• 然后再找出收益最接近10倍，100倍，1000倍的年份指给土豪。
• 土豪一看第4年、第7年、第10年就肯定超过预期收益，非常高兴！

经理用这张表查找收益，再找到最接近收益的大体年份的过程，就是利息的逆运算，是最简单的对数运算，这个表就是对数表的雏形。

其实这和我们根据加法表进行减法运算、根据乘法表进行除法运算是同一个道理。

例如知道了3×7 = 21，就可以很快知道21÷3 = 7的除法逆运算结果了。好了，放松一下大脑，继续回来穿越历史。

三、对数发明的历史

据说4000多年前，古巴比伦时代的人们就发明对数和对数表了，但因为我没找到资料证实，只能从近代开始。

16、17世纪，英、法加入了大航海的行列，开始了美洲殖民地的开拓，远洋贸易变得日益频繁。那时的人们已经知道地球是球形，大海上船只的位置靠经纬度来确定。

纬度测定很容易，几千年前人们就知道，通过测量北极星的仰角，可以估算出船已经在南北方向航行了多远。但是经度的测量不是一般的困难。在茫茫的大洋上，如果无法准确测定船只的经度，代价会极为高昂。

经度的精确测量问题直到18世纪才得到有效解决，这归功于约翰·哈里森发明了高精度机械钟表。这段历史还被拍成了电影和记录片，推荐一本精彩的书《经度：一个孤独的天才解决他所处时代最大难题的真实故事》和罗辑思维的节目《击溃牛顿的钟表匠》。

但是在哈里森之前的数百年里，人们只能求助于天文学家来解决，因为天空就是人们最早、最精确的钟表，太阳、月亮、星星等天体就是上面的表针，读懂这个钟表，就可以知道时间和经度了。

天文学家观测天体，计算出运行的轨道，来预测未来几年每个时间点上天体所在的精确位置，英国天文学家以格林尼治天文台的时间为基准，再把时间和天体位置整理成详细的表格，公开出版发行。这套星表可不便宜，星表加上六分仪售价约20英镑，相当于现在2万人民币，即便这样也经常脱销。海上的人用六分仪测量天体，再去查那本高价天文表格，求得当地时间和格林尼治时间，知道两地的时间差，就知道现在的经度了。

16世纪和17世纪之交，天文学家第谷和开普勒通过大量的观测，绘制了当时最精确的星图，解决了天文学家天文数据精度不足的难题。有了高精度的星图，全欧洲的数学家开始了天体轨道的计算竞赛，很多科学家也因此获得了商业和学术上的丰厚回报。那时的天文学家、数学家可不是像现代这么冷门，更像当今那些IT、金融等热门行业里的精英一样，享受着人人羡慕的不菲高薪。

顺便说一下，日心说之所以能取代地心说，也是因为日心说模型更简洁，不仅计算起来更简单，而且预测非常准确，可以很好的解释行星逆行等现象，这是地心说完全做不到的。

即使这样，要想预测天体的运行，其计算也是极其繁琐和浩瀚的，在解决计算问题时，数学家们发明了大量崭新的数学理论和计算工具，包括对数、解析几何、微积分和牛顿力学等伟大的创新。可以说天文学是当时科学界最闪亮的宝石，是当时的高科技热门产业。其中，对数的发明人就是约翰·纳皮尔

纳皮尔是天文学家、数学家，在计算轨道数据时，也被浩瀚的计算量所折磨。

看起来在数学实践中，最麻烦的莫过于大数字的乘法、除法、开平方和开立方，计算起来特别费事又伤脑筋，于是我开始构思有什么巧妙好用的方法可以解决这些问题。

--约翰·纳皮尔，《奇妙的对数表的描述》（1614）   《e的故事：一个常数的传奇 》

但纳皮尔不是一般人，不想像IT民工一样苦逼的重复劳动，于是用了20年的时间，进行了数百万次的计算，发明了对数和对数表，堪称学霸中的战斗机。

为了理解对数计算的优势，我们通过案例来说明，下面的表格里有两个数列：

第1行是自然数，他们是等差的；

第2行是2的倍数，他们是等比的；

要计算第2行的等比数列中任意两个数的乘积，例如16x64；

先到第1行的等差数列，寻找对应的数，16对应4，64对应6；

然后做加法，4+6 = 10，再查找10所对应等比数列的1024；

得到计算结果就是16x64 = 1024

借助这个表，仅靠心算就可以用4+6 = 10的加法，完成麻烦的16×64乘法。

同样也可以进行除法变减法的运算，把1024/128，变为10-7 = 3，对应结果为8。

把这个表变的更长，就可以计算数值更大的乘法，这个表就是极度简化的对数表。

把直尺掰弯了就成了柱状算尺，像不像风水大师的道具？

四、微分中的e

有人说：我不懂微积分，估计看不懂！没关系！你可以这样理解，积分是升维的过程，微分是降维的过程。

例如

把一张张纸叠起来变成厚厚的词典，这是从2维变成3维的升维，这是积分；

把一大块羊肉，切成一片片羊肉片，就是从3维为变2维的降维，这是微分。

在微积分中，底数为e的指数函数e^x，其导数还是这个函数e^x，也就是不论求多少次导数，其导数就像一个常量一样永远是恒定的。不知道别人的感觉如何，反正我第一次知道时是很惊奇的。

举个例子：

西瓜都切过吧？

无论你怎么切一个实心球，其横截面都是圆面，也就是3维降2维，还是和圆有关。

2维的圆面也是有很多1维的同心圆组成，也就是2维降1维，还是和圆有关。

如上所说，球被降维了2次还是和圆有关，π这个常数你是甩不掉的。

这一点对更高维度的球也适用，参见n维球面。

e^x也是这样，而且比球面更厉害。无论如何降维，e^x总是老样子，一点儿都没变！

就好像你切掉孙悟空的一部分，你以为是一小片肉，睁眼一看，居然是另一个孙悟空，而且一样大！

这种自相似或全息性太匪夷所思、太好玩儿了！大刘！我知道怎么化解《三体》外星人的降维攻击了！

下面就是e^x在直角坐标系中的样子

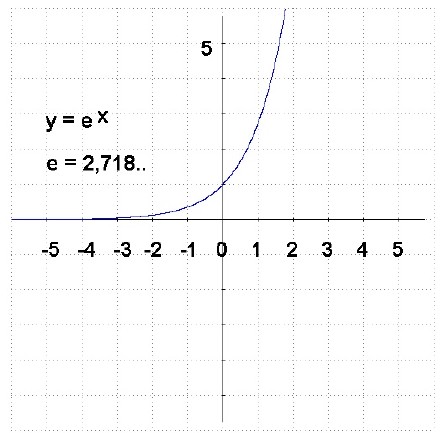
美妙的螺线

在上面的部分中，指数函数e^x的美并没有真正的体现出来。让我们换一个视角看，你一定会大吃一惊。

我们知道二维坐标系除了直角坐标系外，还有一种常用的是极坐标系，如下图所示。

我们把指数函数e^x换成极坐标，就变成了e^θ，θ是点与极轴的夹角。

这时的指数函数就会变成下图的样子，这个螺线叫对数螺线（Logarithmic spiral），又叫等角螺线。

之所以叫等角螺线，是因为在极坐标中，螺线和射线的夹角始终是一个固定夹角，如下图所示，蓝线每次穿过射线时，其夹角是固定的，也就是等角，我们在后面会用到这个等角特性。

斐波那契数列就是1，1，2，3，5，8，13，21，34，55，89……这样的数列。

其特点是前两个数加起来就是下一个数，例如

1+1 = 2

1+2 = 3

2+3 = 5

……

34+55 = 89

……

用这些数画出来的半圆，可以拼接成下面的螺线形状，这就是斐波那契螺线。

有趣的是这个数列还和黄金比例有关，例如55/34 ≈ 1.6176，接近黄金分割比例1.618，数列的数字越到后面，结果就越趋近于黄金分割这个无理数，如下图

不过斐波那契螺线仅仅是对一种叫黄金螺线（Golden spiral）的近似，黄金螺线是一种内涵黄金分割比例的对数螺线e^θ，下图红色的才是黄金曲线，绿色的是“假黄金螺线”（斐波那契螺线），近似却不重合。

很多科学家发现对数螺线e^θ在自然界中广泛存在。从大如星系、台风，到小如花朵、海螺……宇宙中到处都是对数螺线e^θ的身影。

原来e以这种特殊的方式隐藏在自然之中。需要注意的是，这不是e被称为自然底数的原因，这和大自然没太大关系。

五、自然界中的对数螺线

因为对数螺线具有等角性，受环境影响，很多直线运动会转变为等角螺线运动。

我们以飞蛾扑火为例：

亿万年来，夜晚活动的蛾子等昆虫都是靠月光和星光来导航，因为天体距离很远，这些光都是平行光，可以作为参照来做直线飞行。如下图所示，注意蛾子只要按照固定夹角飞行，就可以飞成直线，这样飞才最节省能量。

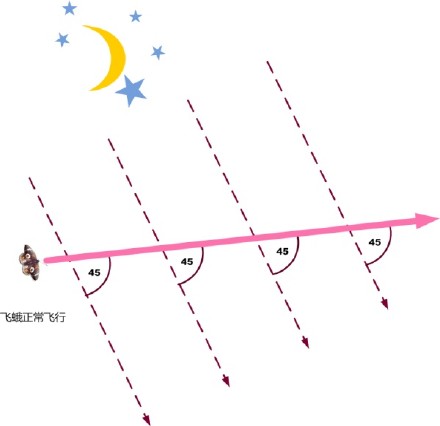
但自从该死的人类学会了使用火，这些人造光源因为很近，光线成中心放射线状，可怜的蛾子就开始倒霉了。

蛾子还以为按照与光线的固定夹角飞行就是直线运动，结果越飞越坑爹，飞成了等角螺线，最后飞到火里去了，这种现象还被人类称为昆虫的正趋光性。

蛾子说：趋你妹的光啊，傻瓜才瞪着光飞，不知道会亮瞎眼啊？！！

我们完全被人类误导了，亿万年才演化出的精妙直线导航方法，被人类的光污染干扰失效了！

不用假慈悲的飞蛾扑火纱罩灯了，赶紧把灯关了吧！

注意下图飞虫都在做螺线飞行，如果昆虫有趋光性。直飞不是更好吗？

不要以为只有蛾子会这样，人在用指南针导航时也有同样的问题，因为篇幅太长就不展开了，有兴趣请移步《既然昆虫有趋光性，为什么昆虫不齐刷刷地奔向太阳？》。

根本原因是原来作为参考的平行场变成了中心发散的场，导致直线运动变成了螺线运动。

我们也知道，绝对平行的场在自然界中是不存在的，只是我们为了计算方便，在小范围内近似认为平行而已。如果把尺度放大了看，更多的场是不平行的、是发散的，所以自然界中大量存在等角螺线现象就很正常了。

例如理想状态下，流体应该是直线运动的，但在发散场和地球自转的作用下，就会像飞蛾一样走出类似等角螺线的形状，天上的台风和水中的漩涡就是这样形成的，不过实际情况远比这要复杂，只能近似这样考虑。

六、C代码输出斐波那契数列

#include "stdio.h"

void fobanacci(int n);
int main(void)
{
  int n;
  printf("输入你所要的斐波那契数项数（输入任何字母退出）：");
  while(scanf("%d",&n)==1)
  {
    if(n<1)
      printf("\n请输入大于0的整数\n");
    else if(n>50)
        printf("\n请输入小于51的整数\n");
    else
    {
        printf("\n你得到的斐波那契数列如下：\n0\n");
        fobanacci(n);
    }
    putchar('\n');
    printf("输入你所要的斐波那契数项数（输入任何字母退出）：");
  }
  printf("拜拜！\n");
  return 0;
}

void fobanacci(int n)
{
  int f1=0,f2=1,f3=0,i;

  for(i=1;i小于n;i++)
  {
    f3=f1+f2;
    f1=f2;
    f2=f3;
    printf("%d\n",f3);
  }
  return;
}

---

人间有味是清欢，诗酒趁年华。觉得不错，动动发财的小手点个赞哦！