开平方的快速算法(C代码)

目录：

一、牛顿迭代法

二、采用移位、加减法实现

三、效率高于牛顿迭代法的开平方

1、原理

2、实现代码

四、卡马克快速开平方算法

1、C-Free模拟验证卡马克开平方

2、实际的项目应用

3、卡马克快速开平方的由来

---

一、牛顿迭代法

牛顿迭代法：多数方程不存在求根公式，牛顿提出了一种用迭代来求方程近似根的方法。思路就是不断取切线，用线性方程的根逼近非线性方程 f(x) = 0 的根 X*。

图1.1 牛顿迭代法求开方

过点 (Xk,f(Xk)) 作函数的切线，切线方程是：。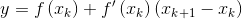

切线与 x 轴的交点是 Xk+1，点 (Xk+1,0) 满足以下方程：。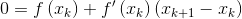

如果 f'(Xk) ≠ 0，则有    这就是牛顿迭代法的迭代公式。

//C语言 abs()是取绝对值
#include "math.h"
int mySqrt(int x)
{
    if( x==0 )
        return 0;
    
    double xk = 1, xk1 = 0; 
    double err = 1e-6; // err为误差，1e-6就是1乘10的-6次幂
    
    while( abs(xk-xk1) > err ) //循环退出的条件是真正解与近似解的误差进入允许的范围
    {
        xk1 = xk;
        xk = ( xk + x/xk )/2; //迭代公式
    }
    return xk;
}

#include "math.h"
int mySqrt(int x)
{
    long xk = x; //避免 xk*xk 溢出，故采用long整型
    double err = 1e-6; // err为误差，1e-6就是1乘10的-6次幂
    
    while( xk*xk > x ) //循环退出的条件是 xk*xk 小于 x ，参考本文代码1中的区间关系
    {
        xk = ( xk + x/xk )/2; //迭代公式
    }
    return xk;
}

#include "math.h"
double sqrt(double x)
{
    if (x == 0)
        return 0;
    
    double last = 0.0;
    double res = 1.0;
    
    while (res != last)
    {
        last = res;
        res = (res + x / res) / 2;
    }
    return res;
}

/*
==================================================================
使用牛顿迭代法求a的平方根，迭代公式：Xn+1 = (Xn+a/Xn)/2.
先输入符合条件的数a，给x0和x1赋值，使得差的绝对值>10^(-10)；
当差 ≥10^(-10) 时使用迭代公式使 x0 和 x1 的差 <10^(-10)方，则平方根就是x1或x0。
==================================================================
*/
#include "stdio.h"
#include "math.h"

int main(void)
{
    float a,x0,x1;

    printf("a=");
    scanf("%f",&a);
    if(a >= 0)
       flag = 0;
    else
       printf("你所输入的数不能求平方根，请重试！\n_________________\n\n");
    
    x0 = 1;
    x1 = x0+1;
    
    while(fabs(x0-x1) >= 1e-10)
    {
        x0 = x1;
        x1 = 0.5*(x0+a/x0);
    }
    printf("%.2f的平方根是：%.2f\n",a,x1);
}

二、采用移位、加减法实现

本算法只采用移位、加减法、判断和循环实现，因为它不需要浮点运算，也不需要乘除运算，因此可以很方便地运用到各种芯片上去。

我们先来看看10进制下是如何手工计算开方的。先看下面两个算式：x = 10*p+q ①

公式①左右平方之后得：x² = 100*p² + 20pq + q² ②

现在假设我们知道 x² 和 p，希望求出 q 来，求出了 q 也就求出了 x² 的开方 x 了。

我们把公式②改写为如下格式：q = (x²-100*p²)/(20*p+q) ③

这个算式左右都有 q，因此无法直接计算出q来，因此手工的开方算法和手工除法算法一样有一步需要猜值。我们来一个手工计算的例子：计算 1234567890 的开方。

首先我们把这个数两位两位一组分开，计算出最高位为 3。也就是③中的 p，最下面一行的 334 为余数，也就是公式③中的(x²​​​​​​​ - 100*p²)近似值。

3     ---------------   |12 34 56 78 90  9   ---------------       | 3 34

下面我们要找到一个0-9的数q使它最接近满足公式③。我们先把p乘以20写在334左边：

3q   ---------------   | 12 34 56 78 90 9   ---------------   6q |3 34

我们看到q为5时(60+q*q)的值最接近334，而且不超过334。于是我们得到：

35   ---------------   | 12 34 56 78 90 9   ---------------   65|3 34  |3 25    ---------------    9 56

接下来就是重复上面的步骤了，这里就不再啰嗦了。

这个手工算法其实和 10 进制关系不大，因此我们可以很容易的把它改为二进制，改为二进制之后，公式③就变成了：q = (x²​​​​​​​ - 4*p²)/(4*p+q) ④

我们来看一个例子，计算100(二进制1100100)的开方：

1010 ---------------  |1 10 01 00 1 --------------- 100| 0 10 | 0 00  ---------------  |10 011001| 10 01 ---------------  0 00

这里每一步不再是把 p 乘以 20 了，而是把 p 乘以 4，也就是把 p 右移两位，而由于 q 的值只能为 0 或 1，所以我们只需要判断余数 (x²​​​​​​​-4*p²) 和 (4*p+1) 的大小关系，如果余数大于等于 (4*p+q) 那么该上一个 1，否则该上一个 0。

下面给出完成的 C 语言程序，其中 root 表示 p，rem 表示每步计算之后的余数，divisor 表示 (4*p+1)，通过 a >> 30 取 a 的最高 2 位，通过 a <<= 2 将计算后的最高 2 位剔除。其中 root 的两次 <<1 相当于 4*p。程序完全是按照手工计算改写的，应该不难理解。

unsigned short sqrt(unsigned long a)
{
   unsigned long rem = 0;
   unsigned long root = 0;
   unsigned long divisor = 0;
   
   for(int i=0; i<16; i++)
   {
     root <<= 1;
     rem = ((rem << 2) + (a >> 30));
     a <<= 2;
     divisor = (root<<1) + 1;
     
     if(divisor <= rem)
     {
       rem -= divisor;
       root++;
     }
   }
   return (unsigned short)(root);
}

三、效率高于牛顿迭代法的开平方

目前开平方的方法大部分使用牛顿迭代法。查了一些资料以后找到了一个比牛顿迭代法更加快速的方法。介绍给大家，希望会有些帮助。

1、原理

因为排版的原因，用 pow(X,Y) 表示 X 的 Y 次幂，用 B[0]，B[1]，...，B[m-1] 表示一个序列，其中 [x] 为下标。

假设：
    B[x],b[x]都是二进制序列，取值 0 或 1。
    M = B[m-1]*pow(2,m-1) + B[m-2]*pow(2,m-2) + ... + B[1]*pow(2,1) + B[0]*pow(2,0)
    N = b[n-1]*pow(2,n-1) + b[n-2]*pow(2,n-2) + ... + b[1]*pow(2,1) + n[0]*pow(2,0)
    pow(N,2) = M

(1) N 的最高位 b[n-1] 可以根据M的最高位 B[m-1] 直接求得。

    设 m 已知,因为 pow(2, m-1) <= M <= pow(2, m)，所以 pow(2, (m-1)/2) <= N <=pow(2, m/2)

    如果 m 是奇数，设m=2*k+1,那么 pow(2,k) <= N < pow(2, 1/2+k) < pow(2, k+1),n-1=k, n=k+1=(m+1)/2

    如果 m 是偶数，设m=2k,那么 pow(2,k) > N >= pow(2, k-1/2) > pow(2, k-1),n-1=k-1,n=k=m/2

    所以b[n-1]完全由B[m-1]决定。

    余数 M[1] = M - b[n-1]*pow(2, 2*n-2)

(2) N 的次高位 b[n-2] 可以采用试探法来确定。

    因为 b[n-1]=1，假设 b[n-2]=1，则 pow(b[n-1]*pow(2,n-1) + b[n-1]*pow(2,n-2),2) = b[n-1]*pow(2,2*n-2) + (b[n-1]*pow(2,2*n-2) + b[n-2]*pow(2,2*n-4)),然后比较余数M[1]是否大于等于 (pow(2,2)*b[n-1] + b[n-2]) * pow(2,2*n-4)。这种比较只须根据B[m-1]、B[m-2]、...、B[2*n-4]便可做出判断，其余低位不做比较。

    若 M[1] >= (pow(2,2)*b[n-1] + b[n-2]) * pow(2,2*n-4), 则假设有效，b[n-2] =1；

    余数 M[2] = M[1] - pow(pow(2,n-1)*b[n-1] + pow(2,n-2)*b[n-2], 2) = M[1] -(pow(2,2)+1)*pow(2,2*n-4)；

    若 M[1] < (pow(2,2)*b[n-1] + b[n-2]) * pow(2,2*n-4), 则假设无效，b[n-2] =0；余数 M[2] = M[1]。

(3) 同理，可以从高位到低位逐位求出 M 的平方根 N 的各位。

使用这种算法计算 32 位数的平方根时最多只须比较 16 次，而且每次比较时不必把 M 的各位逐一比较，尤其是开始时比较的位数很少，所以消耗的时间远低于牛顿迭代法。

2、实现代码

这里给出实现 32 位无符号整数开方得到 16 位无符号整数的 C 语言代码。

unsigned int sqrt_16(unsigned long M)
{
     unsigned int N, i;
     unsigned long tmp, ttp;  // 结果、循环计数

     if (M == 0)  // 被开方数，开方结果也为0
         return 0;

     N = 0;
     tmp = (M >> 30);  // 获取最高位：B[m-1]
     M <<= 2;

     if (tmp > 1)   // 最高位为1
     {
         N ++;      // 结果当前位为1，否则为默认的0
         tmp -= N;
     }

     for (i=15; i>0; i--)   // 求剩余的15位
     {
         N <<= 1;     // 左移一位
         tmp <<= 2;
         tmp += (M >> 30);  // 假设
         ttp = N;
         ttp = (ttp<<1)+1;

         M <<= 2;
         if (tmp >= ttp)   // 假设成立
         {
             tmp -= ttp;
             N ++;
         }
     }
     return N;
}

四、卡马克快速开平方算法

1、C-Free模拟验证卡马克开平方

因为工作的需要，要在单片机上实现开平方的操作。卡马克快速开平方据说能比 float sqrt(x) 快 4 倍，下面有详细描述，见本节“3、卡马克快速开平方的由来”。在 C-Free(MinGW及C-Free的使用)下模拟编译通过，计算结果准确度很高。

本例使用的开平方子函数的源码如下：

float SquareRootFloat(float number)
{
    long i;
    float x, y;
    const float f = 1.5F;

    x = number * 0.5F;
    y  = number;
    i  = * ( long * ) &y;
    i  = 0x5f3759df - ( i >> 1 );  //卡马克
//   i  = 0x5f375a86 - ( i >> 1 );  //Lomont
    y  = * ( float * ) &i;
    y  = y * ( f - ( x * y * y ) );
    y  = y * ( f - ( x * y * y ) );
    return number * y;
}

2、实际的项目应用

本项目较详细的介绍移步：STM32单片机-输入捕获、FFT测频，此“卡马克快速开平方算法”在量产的产品中已经实际使用多年(9年以上)。

3、卡马克快速开平方的由来

同志们！本部分如若不感兴趣，可以直接略过哦。取前面的代码使用即可，而且本代码在批量生产的项目中已经验证过。

1）Quake III中求解平方根

任何一个 3D 引擎都是通过其内部的数学模型和实现工具来展现它的力量与速度的，and trust John Carmack of ID software for using really good hacks. 结果，Quake III 中使用了一个非常有意思的技巧来计算平方根倒数 (inverse square root)。 

------------------------------

2）前言

ID Software 最近发布了它的带有 GPL 许可证的 Quake III 引擎源代码，在这篇文章中我们将会看到 Carmark 是怎样用他的 Black Magic 来极其迅速地计算一个浮点数的平方根。 

------------------------------

3）Carmack's不寻常平方根倒数

对文件 game/code/q_math.c 的快速一瞥就显示出了许多有趣的 Performance Hacks。
第一个跳出来的便是对函数 Q_rsqrt 中对 0x5f3759df 的使用，这个数计算了一个浮点数的 inverse square root，但是为什么这个函数有这样的功能呢？观察 q_math.c 原本的函数：

float Q_rsqrt( float number ) 
{ 
  long i; 
  float x2, y; 
  const float threehalfs = 1.5F; 

  x2 = number * 0.5F; 
  y  = number; 
  i  = * ( long * ) &y; // evil floating point bit level hacking 
  i  = 0x5f3759df - ( i >> 1 ); // what the fuck? 
  y  = * ( float * ) &i; 
  y  = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration 
  // y  = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed 

  #ifndef Q3_VM 
  #ifdef __linux__ 
    assert( !isnan(y) ); // bk010122 - FPE? 
  #endif 
  #endif 
  return y; 
} 

它不仅有效，甚至在某些 CPU 上，Carmack 的 Q_rsqrt 比 (float)(1.0/sqrt(x) 的计算快 4 倍，尽管 sqrt() 通常使用的是 FSQRT 的汇编指令！

在另一个文件 code/common/cm_trace.c 中，我们发现了更简洁的对同样 Hack 的实现。这一次，它被用来计算一个 float - sqrt(x) 的平方根。注意，其中的唯一不同是在返回值上：用返回 *y 取代了返回 y。

float SquareRootFloat(float number) 
{
    long i; 
    float x, y; 
    const float f = 1.5F; 

    x = number * 0.5F; 
    y  = number; 
    i  = * ( long * ) &y; 
    i  = 0x5f3759df - ( i >> 1 ); 
    y  = * ( float * ) &i; 
    y  = y * ( f - ( x * y * y ) ); 
    y  = y * ( f - ( x * y * y ) ); 
    return number * y; 
} 

------------------------------

4）牛顿对根的近似值

上面的代码执行了众所周知的牛顿对根的近似值 [3]，像绝大多数其它迭代求近似值的计算一样，牛顿近似值假定是迭代的；每一次迭代都增强了它的准确度直至达到需要的准确度。 

在牛顿近似值中的一般想法是猜测一个数 x 的平方根值 y，可能通过一个简单的操作，用 x/y 拉平 y 来取得更好的猜测，使其更接近实际的平方根。例如，像下面这样计算 2 的平方根，假定初始的猜测是1： 

2/1 = 2 ;  (2 + 1) / 2 = 1.5 

2/1.5 = 1.3333; ( 1.5 + 1.3333 ) / 2 = 1.4167 

2/1.4167 = 1.4117;  ( 1.4167 + 1.4117 ) / 2 = 1.4142 

And so on... 

如前面所提到的，牛顿的近似值是一个大家所熟知的用以快速计算平方根的方法。但是，Carmack 在初始的猜测中就选取了不寻常的值，彻底加强了准确度并且将 Quake III 中计算所要的值的迭代次数降到了 1 次！

------------------------------

5）魔数

函数中真正有意思的方面是神奇的常量 0x5f3759df，用来计算初始猜测的，在 i  = 0x5f3759df - ( i >> 1 ); 

因此，把输入除以 2 并从神奇常量中减去。这个常数工作起来几乎是完美的——对于一个 low relative error of 10^(-3) 来说只要一次牛顿近似值迭代就够了。如评论中第二次迭代中展示的，这个近似值对 Quake III 引擎来说已经足够了。

结果，这个神奇的常数 0x5f3759df 成了一个迷了，在文章 "Fast Inverse Square Root" [2] ，普度大学的数学家 Chris Lomont 研究了这个常数，用了几种精细的技术，Lomont 想自己用数学方法求出这个常数来，结果令人惊奇——Lomont 用数学方法计算出来的最佳常数 (0x5f37642f) 有一点点不同，并且除了理论上强一些之外，它产生的结果并没有源代码中使用的原始常数好！确实，John Carmack 一定用了天才般的黑盒来找到这个常数。 

只在仅仅从数字上来找的方法中，Lomont 找到了一个更好的常数，这个数比原始的那个强了那么一点点。然而，实践中两个常数产生了大概相同的结果，Lomont 提出这个使用了更好的常数的函数： 

float InvSqrt(float x) 
{
  float xhalf = 0.5f*x; 
  int i = *(int*)&x; // get bits for floating value 

  i = 0x5f375a86- (i>>1); // gives initial guess y0 
  x = *(float*)&i; // convert bits back to float 
  x = x*(1.5f-xhalf*x*x); // Newton step, repeating increases accuracy 
  return x; 
}

---

首先要有一个具体目标，那些所有你认为必须前置的知识，都可以在完成目标的过程中学到。觉得不错，动动发财的小手点个赞哦！