电力-故障分析理论及对称分量法

目录：

一、对称分量法

1、对称分量法介绍

2、对称分量法计算正序、负序、零序

1）CAD作图法   2）Matlab软件计算

二、电力系统故障分析理论

1、电力系统典型故障分析的一般方法

2、单相接地短路K(1)故障分析

3、两相短路K(2)故障分析

4、两相接地短路K(1.1)故障分析

5、三相短路K(3)故障分析

6、总结

三、电网故障定位与隔离(配网自动化)

四、电力-故障录波(向量图)

---

一、对称分量法

1、对称分量法介绍

正常运行的电力系统，三相电压、三相电流均应基本为正相序，根据负荷情况（感性或容性），电压超前或滞后电流1个角度（Φ），如图1。

对称分量法是分析电力系统三相不平衡的有效方法，其基本思想是把三相不平衡的电流、电压分解成三组对称的正序相量、负序相量和零序相量，这样就可把电力系统不平衡的问题转化成平衡问题进行处理。在三相电路中，对于任意一组不对称的三相相量（电压或电流），可以分解为3组三相对称的分量。

---------------

当选择A相作为基准相时，正序时三相相量与其对称分量之间的关系（如电流）为：

IA=Ia1+Ia2+Ia0

IB=Ib1+Ib2+Ib0=α2Ia1+αIa2+Ia0

IC=Ic1+Ic2+Ic0=αIa1+α2Ia2+Ia0

对于正序分量：Ib1=α2Ia1，Ic1=αIa1

对于负序分量：Ib2=αIa2，Ic2=α2Ia2

对于零序分量：Ia0=Ib0=Ic0

式中α为运算子，α=1∠120°，有α2＝1∠240°, α3＝1, α+α2+1=0（此处α^2=α2，即(-1/2+√3/2j)^2=-1/2-√3/2j）

---------------

由各相电流求电流序分量：

I1=Ia1= 1/3(IA +αIB +α2 IC)

I2=Ia2= 1/3(IA +α2 IB +αIC)

I0=Ia0= 1/3(IA +IB +IC)

以上3个等式可以通过代数方法或物理意义（方法）求解。 以求解正序电流为例，对物理意义简单说明，以便于记忆：求解正序电流，应过滤负序分量和零序分量。参考图2，将IB逆时针旋转120°、IC逆时针旋转240°后，3相电流相加后得到3倍正序电流，同时负序电流、零序电流被过滤，均为0。故Ia1= 1/3(IA +αIB+α2 IC)。

---------------

实例说明：

例1、对PMC-6510仅施加A相电压60V∠0°，则装置应显示的电压序分量为：U1=U2=U0=1/3UA=20V∠0°

例2、对PMC-6510施加正常电压，UA＝60V∠0°，UB＝60V∠240°，UC＝60V∠120°，当C相断线时，U1=？U2=？U0=？
解：

U1=Ua1= 1/3(UA +αUB +α2UC)=1/3(60V∠0°+ 1∠120°*60V∠240°)

                                                    =40∠0°（当C相断线时，接入装置的UC=0）

U2=Ua2= 1/3(UA +α2 UB +αUC)=1/3(60V∠0°+ 1∠240°*60V∠240°)

                                                     =20∠60°

U0=Ua0= 1/3(UA + UB +UC)=1/3(60V∠0°+ 60V∠240°)

                                               =20∠300°

-----------------------------

电力系统中的发电机、变压器、电抗器、电动机等都是三相对称元件，经过充分换位的输电线基本上也是三相对称的。对于这种三相对称系统的分析计算可以方便地用单相电路的方法求解。

任何不对称的三相相量 A，B，C 可以分解为三组相序不同的对称分量：正序分量A1，B1，C1，负序分量A2，B2，C2，零序分量A0，B0，C0。即存在如下关系： 在计算电力系统不平衡情况下引用了对称分量法，即任何三相不平衡的电流、电压或阻抗都可以分解成为三个平衡的相量成分即正相序（UA1、UB1、UC1）、负相序（UA2、UB2、UC2）和零相序（UA0、UB0、UC0），即有：UA=UA1+UA2+UA0，UB=UB1+UB2+UB0，UC=UC1+UC2+UC0，

其正相序的相序（顺时方向）依次为UA1、UB1、UC1，大小相等，互隔120度；负相序的相序（逆时方向）依次为UA2、UB2、UC2，大小相等，互隔120度；零相序大小相等且同相，各相序都是按逆时针方向旋转。在对称分量法中引用算子a，其定义是单位相量依逆时针方向旋转120度，则有：UA0=1/3（UA+UB+UC），

UA1=1/3（UA+αUB+α2UC），UA2=1/3（UA+α2UB+αUC）注意以上都是以A相为基准，都是矢量计算。

知道了UA0实际也知道了UBO和VCO，同样知道了UA1也就知道了UB1和UC1，知道了UA2也就知道了UB2和UC2。

2、对称分量法计算正序、负序、零序

1）CAD作图法

(1)正序求解：A相向量不动，B相逆时针转120度，C相顺时针转120度，转动后的A、B、C三向量矢量和的三分之一，为正序。

---------------

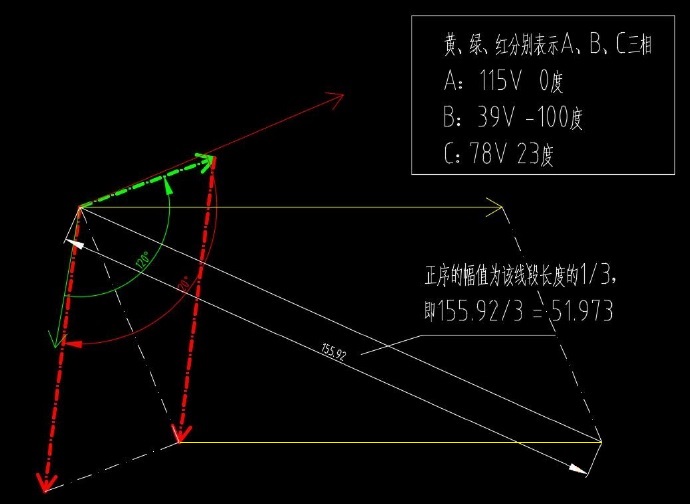
(2)负序求解：A相向量不动，B相顺时针转120度，C相逆时针转120度，转动后的A、B、C三向量矢量和的三分之一，为负序。

---------------

(3)零序求解：A、B、C三向量矢量和，为零序。

-----------------------------

2）Matlab软件计算

clear; clc; %清空变量缓存区；清屏；
syms x; %自定义变量，用于后面计算算子之用
%模式： xxx = [幅值，角度角]
Phase_A = [123,0];
Phase_B = [39,-100];
Phase_C = [78,23];
a = Phase_A(1)*exp( deg2rad(Phase_A(2)) *1i); %将A向量转换为欧拉公式的形式
b = Phase_B(1)*exp( deg2rad(Phase_B(2)) *1i); %将B向量转换为欧拉公式的形式
c = Phase_C(1)*exp( deg2rad(Phase_C(2)) *1i); %将C向量转换为欧拉公式的形式
%deg2rad 角度->弧度
%exp 数组中的每个元素返回指数ex，此处ex=exp( deg2rad(Phase_A(2)) *1i(1i虚数单位i)

temp = solve(x^3-1,x); %对方程求解
k = temp(3); %取第2象限的值为算子
U1 = (a + k*b + k^2*c)/3; %计算正序分量
U2 = (a + k^2*b + k*c)/3; %计算负序分量
U0 = (a + b + c); %计算零序分量
U1 = round(double(norm(U1)),3); %对正序值 四舍五入后重新赋值
U2 = round(double(norm(U2)),3); %对负序值 四舍五入后重新赋值
U0 = round(doub