内容包括行列式求解(含行列式C代码)，电子信息工程虚数直观图解，三角函数应用实例，Matlab求定积分与不定积分，多个公式推导等。紫色文字是超链接，点击自动跳转至相关博文。持续更新，原创不易！
目录：
一、行列式与克莱姆法则
1、前言
2、定义行列式的目的
3、定义行列式的思路
4、低阶行列式
1）二阶行列式 2）三阶行列式
5、行列式的定义
1）全排列 2）逆序数 3）定义三阶行列式 4）n阶行列式的定义
6、克莱姆法则★
1）二元与三元方程组的规律 2）克莱姆法则的定义
7、行列式C代码
二、虚数的直观图解
1、前言
2、什么是虚数★
3、虚数的定义
4、虚数的作用：加法
5、虚数的作用：乘法
1）例1、船的航向 2）例2、计算复功率
6、虚数乘法的数学证明
三、三角函数
1、求圆的半径
1）破碎的圆片 2）确定PCB的圆弧★
2、辅助角
3、求解单摆高度差
四、Matlab求定积分与不定积分
1、Matlab求不定积分
2、Matlab求定积分
五、公式推导
1、三角形、梯形面积推导
2、球形面积推导
1）圆的面积 2）球形面积 3）平方反比定律★
3、一元二次方程根推导
4、欧拉公式推导★
1）欧拉公式的由来 2）欧拉公式的变换 3）欧拉公式的图形
5、算数平均值≥几何平均值
一、行列式与克莱姆法则
1、前言
行列式是线性变换的伸缩因子，数学-线性代数。
本文想谈的是行列式在历史中是怎么演变出来的，主要以下几个问题：
- 定义行列式的目的是什么？
- 行列式出现的思路是什么？
- 为什么用“全排列”、“逆序数”这么晦涩的名词来定义行列式？
2、定义行列式的目的
历史上，定义行列式的目的就是为了解线性方程组。
下面这个方程组：
从几何上来讲，两个方程都是直线，解就是它们的交点：
通过高斯消元法可以得到唯一解：
一般的，对于二元一次线性方程组：
如果它有唯一解，那么通过高斯消元法容易得到：
对于三元一次线性方程组：
如果它有唯一解，同样可以通过高斯消元法得到：
n 元一次线性方程组的解可想而知，会更加复杂。
简化n元一次线性方程组的解，找出其中的规律，在这个过程中产生了行列式。
3、定义行列式的思路
有点像经常说的，大胆假设、小心求证。下面我们来看看这一过程。
4、低阶行列式
1）二阶行列式
（1）定义
二阶行列式是这么定义的，交叉相乘，之后相减：
（2）验证
再看看刚才的二元一次方程组的解：
它的解的分母都是：
套用刚才定义的二阶行列式的符合和规则可以得到：
分子可以分别表示为：
则线性方程的解表示为：
经过验证，这样定义二阶行列式是合理的，可以达到我们预设的解线性方程组的目的。
-------------------------------
2）三阶行列式
（1）定义
比较复杂，可以靠对角线法则进行记忆：
（2）验证
有了三阶行列式的定义，则三元方程组的解：
可以通过三阶行列式来表示：
求解类似于第一个图：
经过验证，这样定义三阶行列式也是合理的。
5、行列式的定义
n 阶行列式应该怎么定义？
具体的过程肯定是，数学家们(应该是凯莱、范德蒙这些先驱)废了无数草稿纸，反复验算各阶线性方程组，从中总结出来的。
为了介绍行列式的定义，先引入两个概念。
-----------------------------------------
1）全排列
有如下三个数字：1，2，3
总共有以下6种不重复的排列方式：
1，2，3 1，3，2 2，1，3
2，3，1 3，1，2 3，2，1
这就是全排列。
把 n 个不同的元素排成一列，叫做这 n 个元素的全排列(简称排列)。
再举个例子，如下四个数字：1，2，3，4
总共有以下 24 种不重复的排列方式，可以自行验算。
-------------------------------
2）逆序数
比如有这么一个数列：3，2，5，4，1
规定：从小到大为正序，否则为逆序
比如：
上图中可以看出，没有一个逆序的，因为 5 是第三个数字，所以用下列的负号来表示没有逆序：t3 = 0
再比如：
数列内所有的逆序数为：
逆序数定义为：
在一个排列中，如果一对数的前后位置与大小顺序相反，即前面的数大于后面的数，那么它们就称为一个逆序。 一个排列中逆序的总数就称为这个排列的逆序数。
再比如数列：3，1，4，5，2
数列的逆序数为 4，可以自行验证。
-------------------------------
3）定义三阶行列式
通过全排列和逆序数，就可以定义行列式了。
以三阶行列式为例：
来观察每一项的脚标，脚标第一项都是按照 “1，2，3” 排列的：
而脚标的第二项是 “1，2，3” 的全排列：
正负号怎么来的呢？是由逆序数决定的：
整个过程为：
三阶行列式可以定义为：
这种定义方式和之前的对角线定义方式得到的结果是一样的，但是可以推广到 n 阶。
-------------------------------
4）n阶行列式的定义
6、克莱姆法则★
那么上面的 n 阶行列式的定义是否合适？我们用克莱姆(又译作克拉默)法则来验收。加百列·克莱姆，瑞士数学家，他发现了可以通过行列式解线性方程组的克拉姆法则(Cramer's Rule)，让行列式成为数学界的共识，是行列式的历史源头。其应用移步：热敏电阻温度检测-分段曲线拟合之2、分段曲线拟合。
下面从具体的二元、三元一次方程组说起。
-------------------------------
1）二元与三元方程组的规律
观察二元方程组的解：
再观察三元方程组的解：
可以看到如下规律：
- 分母都是系数组成的行列式
- 分子也是系数组成的行列式，只是对应于不同的 xi，第i列被替换为了常数项
推广到 n 元线性方程组的话，就是克莱姆法则。
-------------------------------
2）克莱姆法则的定义
从 n 阶行列式的定义出发可以证明：
这就说明行列式的定义是成功的(从行列式的定义出发，需要先证明几个行列式的性质，然后证明克拉默法则，这里就不引用了)。
为什么要用“全排列”、“逆序数”这么晦涩的名词来定义行列式？完全是因为只有这样定义，克拉默法则才能成立。
7、行列式C代码
#include "stdio.h"
#include "stdlib.h"
#define MAX 9 //定义最大为9阶行列式
int Fun(int n, int a[MAX][MAX]); //函数声明
int main(void)
{
int n = 0; //初始化阶数n
int i = 0, j = 0; //i,j分别表示行与列
int a[MAX][MAX] = {{0}}; //定义行列式
printf("Please input order of determinant,end with a return!");
printf("\n");
scanf("%d",&n); //读入阶数
while(n != 0) //输入为0时退出程序
{
for(i = 0; i < n; i++) //此处2次循环将行列式存入数组中
{
for(j = 0; j < n; j++)
scanf("%d", &a[i][j]);
}
printf("Value=%d\n", Fun(n, a));
scanf("%d", &n);
}
return 0;
}
//以下为计算行列式值的递归函数
int Fun(int n, int a[MAX][MAX])
{
int b[MAX][MAX] = {{0}}; //定义数组b并初始化
int i = 0, j = 0, sum = 0; //i，j为行与列，sum为行列式的值
int x = 0,c = 0,p=0; //用x判断加与减，c,p为中间变量
if(n == 1)
return a[0][0];
for(i = 0;i < n; i++) //此处大循环实现将余子式存入数组b中
{
for(c = 0;c < n-1; c++)
{
for(j = 0;j < n-1;j++)
{
if (c < i)
{//借助c判断每行的移动方法
p = 0; //当p=0时，行列式只向左移，即消去对应的第一列的数
}
else
{//否则行列式左移后再上移
p = 1;
}
b[c][j] = a[c+p][j+1];
}
}
if(i % 2 == 0)
{//i+j(此时j=0，故只考虑i)为偶数，加法预算
x = 1;
}
else
{//i+j为奇数，减法运算
x = (-1);
}
sum += a[i][0] * Fun(n-1,b ) * x; //计算行列式的值
}
return sum; //将值返回
}二、虚数的直观图解
1、前言
我一直觉得虚数 (Imaginary Number) 很难懂。中学老师说，虚数就是 -1 的平方根。
图2.1.1 虚数
可是，什么数的平方等于 -1 呢？计算器直接显示出错！一直都没有真正的理解和认识虚数。
在电子信息工程中充斥着虚数，谁能解释，虚数到底是什么？它有什么用？举个高频电子线路中的例子，如下图电感、电容搭建的阻抗匹配电路，有关内容也可参考电阻/电抗/阻抗/电导/电纳/导纳描述。
图2.1.2 阻抗匹配(Microsoft Visio绘制)
Ic 电流超前电压一个角度，IL 电压超前电流一个 90°，Ic 和 IL 上面有一个点，表示矢量。
bb' 输入阻抗 Zbb' = 600Ω，中心频率 f0 = 83MHz，cc' 输出阻抗 Zcc' = R4 = 50Ω(天线)，Vbb' = V，求取这里的电感和电容值，使得电路的阻抗匹配。(注：在电子行业中，i 通常用来表示电流，故虚数单位用 j 来表示)
解：
Ic = V/(R4+1/jXc3)，若存在一个数，它的倒数等于它的相反数(或者它的倒数的相反数为其自身)，这个数是什么形式？根据这一要求，可以给出方程 -j = (1/j) 。由此得 Ic = V/(R4-jXc3)。
将上式的上下各乘以 R4+jXc3，得 Ic = V(R4+jXc3)/[(R4)²-j²(Xc3)²]。
因为 j² = -1，整理上式最终得 Ic = V(R4+jXc3)/[(R4)²+(Xc3)²]。后面的推算略，更多的计算举例见：三相交流电及其计算之4、复数表示★。
A Visual, Intuitive Guide to Imaginary Numbers – BetterExplained有一篇非常棒的文章《虚数的图解》，这是下文的最终出处。读后恍然大悟，使我终生受益，由是感慨教学方式的不同产生迥异的结果。原来虚数这么简单，一点也不奇怪和难懂！
2、什么是虚数★
首先，假设有一根数轴，上面有两个反向的点：+1和-1。
这根数轴的正向部分，可以绕原点旋转。显然，逆时针旋转 180°，+1 就会变成 -1。
这相当于两次逆时针旋转 90°。
因此，我们可以得到下面的关系式：
(+1) * (逆时针旋转90°) * (逆时针旋转90°) = -1
如果把+1消去，这个式子就变为：
(逆时针旋转90°)² = -1
将"逆时针旋转90°"记为 i ：
i² = -1
这个式子很眼熟，它就是虚数的定义公式。所以，我们可以知道：虚数 i 就是逆时针旋转90°，i 不是一个数，而是一个旋转量；下图中虚数的模值 = A点到O点的距离，根据勾股定理可得。
3、虚数的定义
既然 i 表示旋转量，我们就可以用 i 表示任何实数的旋转状态。
将实数轴看作横轴，虚数轴看作纵轴，就构成了一个二维平面。旋转到某一个角度的任何正实数，必然唯一对应这个平面中的某个点。
只要确定横坐标和纵坐标，比如 (1,1i)，就可以确定某个实数的旋转量 (45°)。
数学家用一种特殊的表示方法，表示这个二维坐标：用 + 号把横坐标和纵坐标连接起来。比如，把 (1,1i) 表示成 1+1i 。这种表示方法就叫做虚数 (complex number)，其中 1 称为实数部，1i 称为虚数部。
为什么要把二维坐标表示成这样呢，下一节告诉你原因。
4、虚数的作用：加法
虚数的引入，大大方便了涉及到旋转的计算。
比如，物理学需要计算"力的合成"。假定一个力是 3 + i ，另一个力是 1 + 3i ，请问它们的合成力是多少？
根据"平行四边形法则"，你马上得到，合成力就是 (3 + i) + (1 + 3i) = (4 + 4i)。这就是虚数加法的物理意义。
5、虚数的作用：乘法
如果涉及到旋转角度的改变，处理起来更方便。
1）例1、船的航向
一条船的航向是 3 + 4i 。如果该船的航向，逆时针增加 45°，请问新航向是多少？
45° 的航向就是 1 + i 。计算新航向，只要把这两个航向 3 + 4i 与 1 + i 相乘就可以了（原因在下一节解释）：
(3 + 4i) * (1 + i) = (-1 + 7i)
所以，该船的新航向是 -1 + 7i 。
如果航向逆时针增加 90°，就更简单了。因为 90° 的航向就是 i ，所以新航向等于：
(3 + 4i) * i = (-4 + 3i)
这就是虚数乘法的物理意义：改变旋转角度。
-------------------------------
2）例2、计算复功率
选取电压电流同方向为关联参考方向时，复功率的相位应当和阻抗的相位一致，因此计算得到的复功率相角为电压减电流。
计算复功率时，电压电流相乘，电流取共轭表示的电压的幅角作为被减数、电流的幅角作为减数，这样才可以得到电压减电流的相角差。
6、虚数乘法的数学证明
为什么一个复数改变旋转角度，只要做乘法就可以了？下面就是它的数学证明，实际上很简单。
任何复数 a + bi，都可以改写成旋转半径 r 与横轴夹角 θ 的形式。假定现有两个复数 a + bi 和 c + di，可以将它们改写如下：
这两个复数相乘，(a + bi)(c + di) 就相当于 r1 * r2 * (cosθ1 + isinθ1) * (cosθ2 + isinθ2)
展开后面的乘式，得到 cosθ1 * cosθ2 - sinθ1 * sinθ2 + i(cosθ1*sinθ2 + sinθ1*cosθ2)
根据三角函数两角和公式，上面的式子就等于 cos(θ1+θ2) + isin(θ1+θ2)
所以 (a + bi)(c + di) ＝ r1 * r2 * [cos(θ1+θ2) + isin(θ1+θ2)]。
这就证明了，两个复数相乘，就等于旋转半径相乘、旋转角度相加。
三、三角函数
1、求圆的半径
1）破碎的圆片
2）确定PCB的圆弧★
有关 PCB 绘制的详细内容移步专栏：线路板、钢网、PCBA。
2、辅助角
在和差化积问题中，有些和差形式的表达式不能直接应用和差化积公式，但引进适当的辅助角后就可容易地将它们化为乘积形式。有关三角函数的知识移步：数学-三角函数。
在一般形式的引人辅助角的变换可以说明如下：将已知数或已知式考虑成某个自变量的三角函数值，这个自变量叫做辅助角(辅助自变量)。
从辅助角的所有可能值的集合中取出一个完全确定的值(例如，绝对值最小的值)。这样选好后，辅助角它的三角函数的给定值，可以完全确定，并且在以后的变换式中就看成是已知的。
3、求解单摆高度差
四、Matlab求定积分与不定积分
直观数学：图解数学，关于Matlab 的部分知识移步：数学工具-Matlab Simulink仿真。
积分相当于求面积
1、Matlab求不定积分
1）首先举一个比较简单的例子，来验证 matlab 求不定积分的功能。
求函数 “xe^x” 的不定积分。
我们要用到 "int" 命令，具体操作见下图。
-------------------------------
2）函数 “xe^x” 的不定积分的结果见下图
实际上，我们要求 f(x) 的不定积分，只需在 matlab 中输入如下命令：
*****命令开始*****
syms x C
int( f(x) ) +C
*****命令结束******
当然上面命令中的 f(x) 为你自己指定
我们还知道一些函数的被积函数是无法用初等函数表示的，比如函数 “sin(x)/x"。
下面我们用 matlab 来求一下函数 “sin(x)/x" 的不定积分。看下图的结果：
2、Matlab求定积分
1）首先举一个比较简单的例子
求函数 "x^2*e^x" 在(0到1)上的积分
输入命令：
*****命令开始*****
syms x
int( x^2*exp(x), 0, 1 )
*****命令结束******
命令见下图：
-------------------------------
2）函数 “x^2*e^x” 在(0到1)的定积分的结果见下图
实际上，我们要求 f(x) 的在 (a到b) 的定积分，只需在 matlab 中输入如下命令：
*****命令开始*****
syms x
int( f(x) , a, b )
*****命令结束******
当然上面命令中的 f(x) 为你自己指定
a 为积分下限，b 为积分上限。
也可以采用 Excel 求取定积分，请移步：Excel画折线图做定积分。
五、公式推导
1、三角形、梯形面积推导
长方形的面积是长方形物体表面的大小或围成长方形平面的大小，计算方法是长乘以宽。将长方形倾斜即可得到平形四边形。
2、球形面积推导
1）圆的面积推导
本内容引自于：X-Ray and Time-Lapse Vision。先让我们看一下周长、面积、表面积和体积的计算公式：
圆盘真的只是一堆戒指放在一起，以下是圆圈区域的“分步”视图：
让我们展开那些卷曲的戒指变成直线，因为它们更容易测量：
我们有一堆拉直的环，形成一个三角形， 这样更容易衡量。因为三角形比圆更容易计算，所以找到面积公式不是太麻烦。即“环形三角形”的面积 = 1/2*底边*高 = 1/2*𝑟*(2𝜋𝑟) = 𝜋𝑟²，即可得到圆的面积公式S圆 = 𝜋𝑟²。
2）球形面积推导
3）平方反比定律★
本内容引自：最美的公式：你也能懂的麦克斯韦方程组(积分篇)。
假设现在有一个点源开始向四面八方传播，因为它携带的能量是一定的，那么在任意时刻能量达到的地方就会形成一个球面。而球面的面积公式 S = 4πr²(r为半径)，它跟半径的平方r²成正比，这也就是说：我们同一份能量在不同的时刻要均匀的分给4πr²个部分，那么每个点得到的能量就自然得跟 4πr² 成反比，这就是平方反比定律的更深层次的来源。在EMC、抗干扰专栏中的辐射发射(RE)具有同样的规律。
因此，如果我们生活在四维空间里，我们就会看到很多立方反比的定律，而这也是科学家们寻找高维度的一个方法。许多理论(比如超弦理论)里都有预言高维度，科学家们就去很小的尺度里测量引力，如果引力在一个很小的尺度里不再遵循平方反比定律，那就很有可能是发现了额外的维度。
3、一元二次方程根推导
4、欧拉公式推导★
圆心为原点 (0，0) 的圆圈数学方程式：
此式转换为通俗易懂的语句：所有点与中心的距离相等。
1）欧拉公式的由来
麦克劳林公式来自微积分基础1-微分篇之8、泰勒Taylor公式及其应用
2）欧拉公式的变换
3）欧拉公式的图形
时域与频域的对应关系(信号与系统)
5、算数平均值≥几何平均值
tanθ = h/a，tanθ = b/h，那么h = √ab，(a+b)/2 ≥ √ab，三角函数。
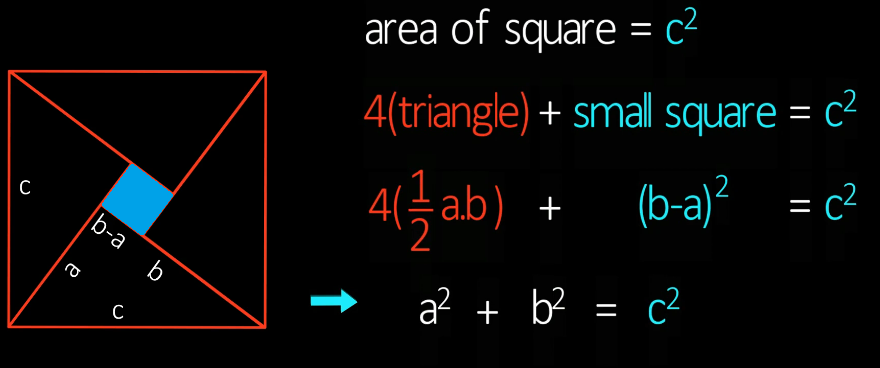
星光不问赶路人，岁月不负有心人。觉得不错，动动发财的小手点个赞哦！
扫一扫
1万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
