【NOIP2013模拟联考2】三角阵(tri) 题解

原题

Description

把3个相同的小三角形按如下方式连接起来就形成了一个一级三角阵。

我们把位于顶端的小三角形标记为T，位于左端的小三角形标记为L，位于右端的小三角形标记为R。

把3个一级三角阵按同样的方式连接起来就形成了一个二级三角阵。

我们为顶端的三角阵的标记添加前缀T，为左端的三角阵的标记添加前缀L，为右端的三角阵的标记添加前缀R。

把3个二级三角阵按同样的方式连接起来就形成了一个三级三角阵。

同样地为顶端的三角阵的标记添加前缀T，为左端的三角阵的标记添加前缀L，为右端的三角阵的标记添加前缀R。

依次类推，可以构建一个N级三角阵。

如果两个小三角形有公共点，则认为这两个小三角形相邻，可以一步到达。

你的任务是求从一个小三角形走到另一个小三角形至少需要多少步。

Input

第一行是三角阵的等级Ｎ（Ｎ≤30）。

第二行和第三行都是一个长度为N的字符串，由大写字母“L”、“R”、“T”组成，表示两个小三角形的标号。

Output

输出一个数，表示从一个小三角形走到另一个小三角形所需的最少步数。

Sample Input

3

TRL

RLR

Sample Output

5

【样例解释】

从“TRL”出发，途经“TRR”、“RTT”、“RTL”、“RLT”，最后到达“RLR”，一共需要5步。

Data Constraint

40% n<=5

100% n<=30

分析

我们先将一个N级三角阵分成三个N-1级三角阵。
若两个点在同一个三角形里面，就继续分。

这时要分类讨论：
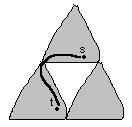
1、通过这两个的连接点。
如下图：

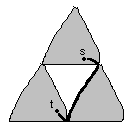
2、通过第三个三角形。
如下图：

• 那现在只需要知道这个点到三边的距离就可以啦。

那怎么求呢？

以这个为例，L到三定点的距离分别是：0，1，1

若现在拓展为二级三角阵，如下图

此时，点TL到三个定点的距离就分别是：2，1，3

那接着拓展，变为三级三角阵

那点TTL到三个定点的距离就分别是：6，1，7

现在应该发现规律了吧。

下面是代码：

#include <cstdio>
#include <algorithm>
#include <cstring>
#include <string.h>
#include <cmath>
#include <math.h>
#define ll long long
using namespace std;

ll z[33],sum1,sum2;
int n;
char s1[33],s2[33];

int main()
{
    freopen("tri.in","r",stdin);
    freopen("tri.out","w",stdout); 

    scanf("%d\n",&n);
    for(int i=1;i<=n;i++)
        scanf("%c",&s1[i]);
    scanf("\n");
    for(int i=1;i<=n;i++)
        scanf("%c",&s2[i]);

    if(s1==s2)
    {
        printf("0\n");
        return 0; 
    } 
    int x=1; 
    while(s1[x]==s2[x])x++;
    if(x==n-1)
    {
        printf("1\n");
        return 0;
    }
    char ch;
    if((s1[x]!='T')&&(s2[x]!='T'))ch='T';else
        if((s1[x]!='L')&&(s2[x]!='L'))ch='L';else
            ch='R';
    z[n]=1;
    for(int i=n-1;i;i--)
        z[i]=z[i+1]*2;
    for(int i=x+1;i<=n;i++)
    {
        if(s1[i]!=s2[x])sum1+=z[i];
        if(s2[i]!=s1[x])sum1+=z[i];
    }
    sum1++;

    for(int i=x+1;i<=n;i++)
    {
        if(s1[i]!=ch)sum2+=z[i];
        if(s2[i]!=ch)sum2+=z[i];
    }
    sum2+=z[x]+1;

    ll ans=min(sum1,sum2);
    printf("%lld",ans);
}