SIFT论文整理

Distinctive Image Featuresfrom Scale-Invariant Keypoints

本文主要是对Lowe SIFT论文的提炼，标注自己阅读论文时需要重点理解的知识点，以备日后回顾时，无需从头看论文。（仅供他人参考）

1. Introduction

• Scale-space extrema detection:
• Keypoint localization
• Orientation assignment
• Keypoint descriptor

2. Related research

…..

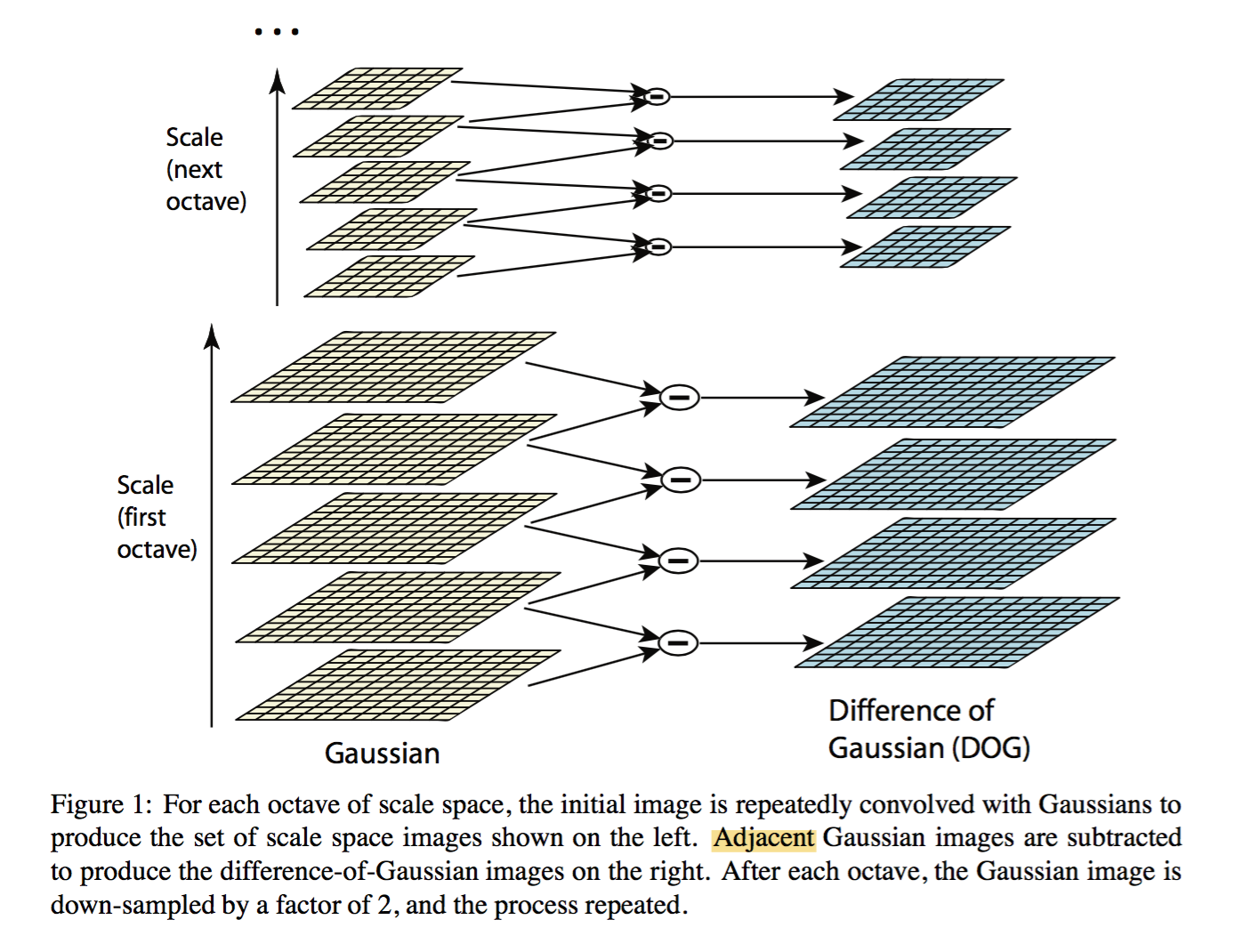
3. Detection of scale-space extrema

Detecting locations that areinvariant to scale change of the image can be accomplished by searching for stable featuresacross all possible scales, using a continuous function of scale known as scale space (Witkin,1983).

• 构建尺度空间
  
• LoG近似DoG找到关键点<检测DOG尺度空间极值点>

3.1 Local extrema detection

In order to detect the local maxima and minima of D(x, y, σ), each sample point is comparedto its eight neighbors in the current image and nine neighbors in the scale above and below(see Figure 2). It is selected only if it is larger than all of these neighbors or smaller than allof them. The cost of this check is reasonably low due to the fact that most sample points willbe eliminated following the first few checks.

3.2 Frequency of sampling in scale

​ To summarize, these ex