严格次小生成树

次小生成树的概念

最小生成树大家应该都不陌生， 次小生成树就是边权和大于等于最小生成树的另一颗树，也就是边权之和第二小的生成树， 有严格次小生成树和非严格次小生成树。
边权之和严格大于最小生成树的且权值最小的树，就是严格次小生成树。
若求得的另一颗树与最小生成树权值相等， 则为非严格的次小生成树。
在本文仅介绍对于严格次小生成树的求法， 其实大同小异

简单求法

前置知识
树边：就是在生成树当中的边
非树边：未连接到该生成树上的边
定理： 对于一张无向图,如果存在最小生成树和次小生成树,那么对于任何一颗最小生成树都存在一颗次小生成树，使得这两棵树只有一条边不同。

假设我们求得了一颗如图的最小生成树， 那我们要如何求次小生成树呢？

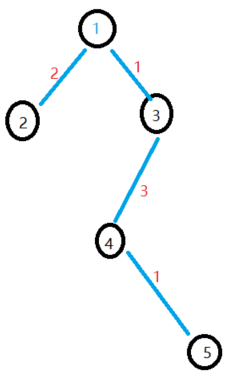
如果我们得到一颗生成树，此时我们无论加入哪一条非树边， 都会构成一个环，如图， 我们加入了连接顶点5<—>3的一条边， 构成了黄色线条指示的环， 那这有什么用呢？

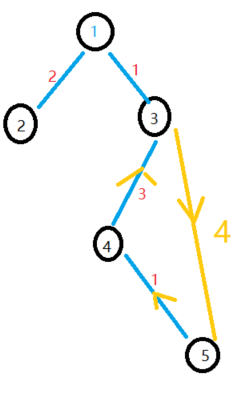
此时， 我们如果在这个环中去掉一条原树边， 便可以构成一颗不同的生成树，我们要求次小生成树， 最优的方案肯定是去掉环中最大的一条边， 但是如果最大树边和我们加入的非树边权值相等， 得到的答案和最小生成树相同怎么办？所以我们还需要加入一条次大边， 如果相等的话， 我们就判断一下删去次大边是不是最优解。

1. 先求出最小生成树， 在求最小生成树的过程中， 将树边建图并标记，记录最小生成树的权值 res
2. 在最小生成树构成的图中依次遍历每个顶点，求出最小生成树中任意两个顶点所通过的路径的最大值dis1[u][v] 和 dis2[u][v]
3. 依次枚举非树边， 若该非树边权值 w[ i ] 大于环中最大边（防止求出非严格的次小生成树）就更新答案 ans = min(ans, res + w - dis1[u][v]) 如果与最大边相等的话， 就采用次大边更新答案 ans = min(ans, res + w - dis2[u][v])

例题

秘密的牛奶运输

参考代码

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 505;
const int M = 1e4 + 10;
typedef long long ll;
int n, m, f[N], dis1[N][N], dis2[N][N];
ll ans = 1e18, res;
int h[N], e[N * 2], wi[N * 2], ne[N * 2], idx;
bool st[M];

struct node {
    int u, v, w;
    bool operator < (const node &b) const {
        return w < b.w;
    }
} edge[M];



int findx(int x) {
    if (f[x] == x)
        return x;

    return f[x] = findx(f[x]);
}

void add(int u, int v, int w) {
    e[++idx] = v;
    wi[idx] = w;
    ne[idx] = h[u];
    h[u] = idx;
}

void dfs(int u, int flag, int max1, int max2, int d1[], int d2[]) {
    d1[u] = max1;
    d2[u] = max2;
    for (int i = h[u]; i; i = ne[i]) {
        int v = e[i], w = wi[i];

        if (v != flag) {
            int x=max1, y=max2;
            if(w > max1)
                y=max1, x=w;  //更改次大值和最大值
            else if(w != x && w > max2)
                y=w;
            dfs(v, u, x, y, d1, d2);
        }
    }
}

int main() {
    scanf("%d%d", &n, &m);

    for (int i = 1; i <= n; i++)
        f[i] = i;

    for (int i = 1; i <= m; i++)
        scanf("%d%d%d", &edge[i].u, &edge[i].v, &edge[i].w);

    sort(edge + 1, edge + 1 + m);

    for (int i = 1; i <= m; i++) {
        int u = edge[i].u, v = edge[i].v, w = edge[i].w;
        u = findx(u), v = findx(v);

        if (u != v) {
            f[u] = v;
            st[i] = true;
            add(u, v, w), add(v, u, w);
            res += w;
        }
    }

    for (int i = 1; i <= n; i++)
        dfs(i, -1, 0, 0, dis1[i], dis2[i]);

    for (int i = 1; i <= m; i++) {
        if (st[i])
            continue;

        int u = edge[i].u, v = edge[i].v, w = edge[i].w;

        if (w > dis1[u][v])
            ans = min(ans, res + w - dis1[u][v]);
            //防止非树边权值和环中最大边相等
            //相等则减去次大边计算
        else if(w > dis2[u][v])
            ans = min(ans, res + w - dis2[u][v]);
    }

    cout << ans << "\n";
    return 0;
}

倍增求法

由于上述做法的搜索路径最大值复杂度过高， 我们还可以通过倍增算法优化求解。引入了倍增算法， 可以去别的博客学习学习， 我就先溜了！~~~

例题

次小生成树

参考代码

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 100050, M=3*N, inf=0x3f3f3f3f;
int n,m,h[N],e[M],ne[M],w[M],idx;
int p[N], d[N], f[N][17], d1[N][17], d2[N][17], q[N];

void add(int u, int v, int x){
    e[++idx]=v;
    w[idx]=x;
    ne[idx]=h[u];
    h[u]=idx;
}

int findx(int x){
    if(p[x]==x) return x;
    return p[x]=findx(p[x]);
}

struct node{
    int a,b,c;
    bool st;
    bool operator <(const node &t) const{
        return c<t.c;
    }
}no[M];

ll Kruskal(){
    for(int i=1; i<=n; i++) 
        p[i]=i;
    sort(no+1, no+1+m);
    ll res=0;
    for(int i=1; i<=m; i++){
        int u=findx(no[i].a), v=findx(no[i].b);
        if(u!=v){
            p[u]=v;
            res+=no[i].c;
            no[i].st=true;
            add(no[i].a, no[i].b, no[i].c);
            add(no[i].b, no[i].a, no[i].c);
        }
        else no[i].st=false;
    }
    return res;
}

void bfs(){
    memset(d, 0x3f, sizeof d);
    d[0]=0, d[1]=1;
    q[0]=1;
    int hh=0, tt=0;
    while(hh <= tt){
        int t=q[hh++];
        for(int i=h[t]; i; i=ne[i]){
            int j=e[i];
            if(d[j] > d[t]+1){
                d[j]=d[t]+1;
                q[++tt]=j;
                f[j][0]=t;
                d1[j][0]=w[i], d2[j][0]=-inf;
                for(int k=1; k<=16; k++){
                    int anc=f[j][k-1];
                    f[j][k]=f[anc][k-1];
                    int dis[4]={d1[j][k-1], d2[j][k-1], d1[anc][k-1], d2[anc][k-1]};
                    d1[j][k]=d2[j][k]=-inf;
                    for(int u=0; u<4; u++){
                        int dd = dis[u];
                        if(dd > d1[j][k])
                            d2[j][k] = d1[j][k], d1[j][k] = dd;
                        else if(dd != d1[j][k] && dd > d2[j][k])
                            d2[j][k]=dd;
                    }
                }
            }
        }
    }
}

int lca(int a, int b, int c){
    static int dis[N*2];
    int cnt=0;
    if(d[a]<d[b]) swap(a,b);
    for(int k=16; k>=0; k--){
        if(d[f[a][k]] >= d[b]){
            dis[cnt++]=d1[a][k];
            dis[cnt++]=d2[a][k];
            a=f[a][k];
        }
    }
    if(a!=b){
        for(int k=16; k>=0; k--){
            if(f[a][k]!=f[b][k]){
                dis[cnt++]=d1[a][k];
                dis[cnt++]=d2[a][k];
                dis[cnt++]=d1[b][k];
                dis[cnt++]=d2[b][k];
                a=f[a][k];
                b=f[b][k];
            }
        }
    }
    dis[cnt++]=d1[a][0];
    dis[cnt++]=d1[b][0];
    int dis1=-inf, dis2=-inf;
    for(int i=0; i<cnt; i++){
        int dd=dis[i];
        if(dd>dis1) dis2=dis1, dis1=dd;
        else if(dd!=dis1 && dd>dis2) dis2=dd;
    }
    if(c>dis1) return c-dis1;
    if(c>dis2) return c-dis2;
    else return inf;
}
int main(){
    scanf("%d%d", &n, &m);
    for(int i=1; i<=m; i++)
        scanf("%d%d%d", &no[i].a, &no[i].b, &no[i].c);
    ll sum=Kruskal();
    bfs();
    ll res = 1e18;
    for(int i=1; i<=m; i++){
        if(!no[i].st){
            int u=no[i].a, v=no[i].b;
            res=min(res, sum + lca(u, v, no[i].c));
        }
    }
    cout << res << "\n";
    return 0;
}