ICP介绍

转：如何用PCL做点云之间的匹配  

2013-08-19 07:16:35|  分类： 默认分类 |  标签： |字号大中小 订阅

http://blog.csdn.net/u010696366/article/details/8941938

PCL Registration API

Registration：不断调整，把不同角度的3D点数据整合到一个完整的模型中。
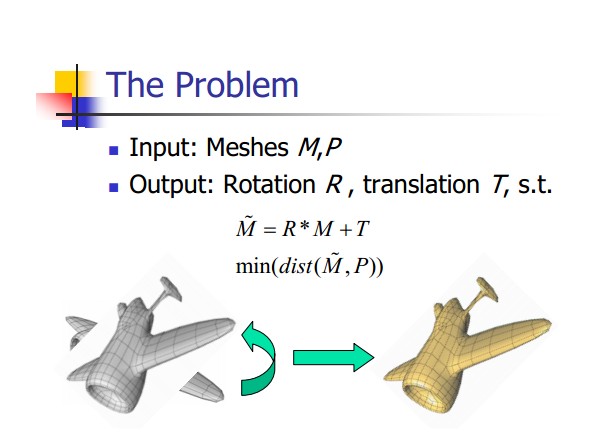
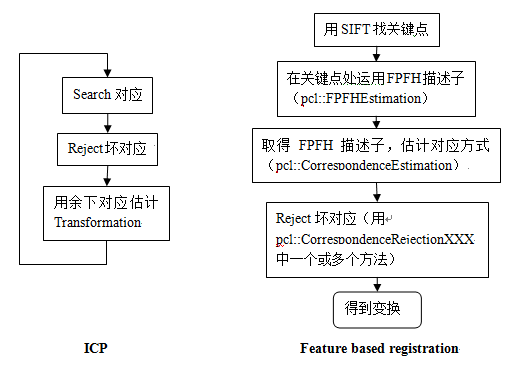
它的目的在于在一个全局坐标系下找到不同视角的定位与定向（两个视角交叉部分重叠完好为最优）。这就是KinectFusion论文中所提到的ICP（ Iterative Closest Point ）算法。给定输入数据集，首先做一个估计，然后通过旋转和平移变换一个数据集，找到一个正确的点集对应方式完美匹配。下面几页PPT是ICP很好的解释。

PCL提供了很多算法，多组点集对应估计，剔除坏对应，稳健的变换估计等。下面详细解释。

Pairwise registration

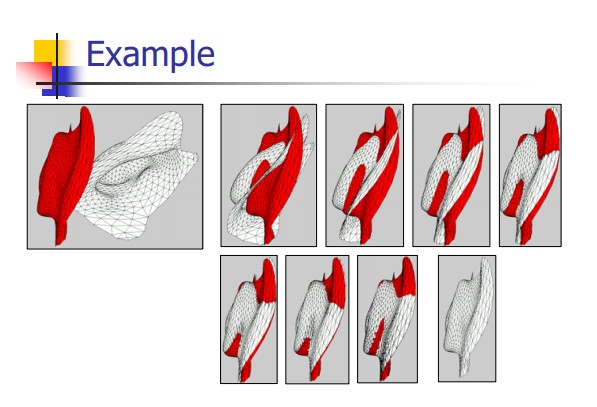
两个点集的对应，输出通常是一个4×4刚性变换矩阵：代表旋转和平移，它应用于源数据集，结果是完全与目标数据集匹配。下图是“双对应”算法中一次迭代的步骤：

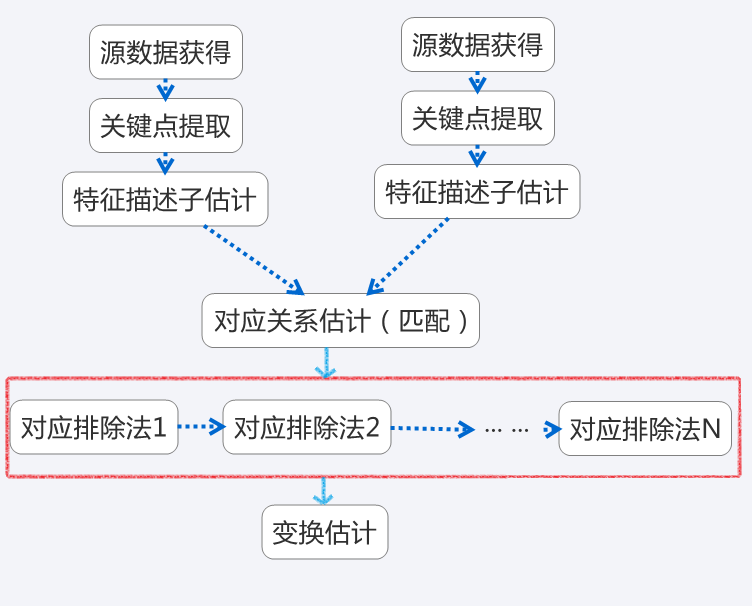
对两个数据源a，b匹配运算步骤如下：

• 从其中一个数据源a出发，分析其最能代表两个数据源场景共同点的关键点k
• 在每个关键点ki处，算出一个特征描述子fi
• 从这组特征描述子{fi}和他们在a和b中的XYZ坐标位置，基于fi和xyz的相似度，找出一组对应
• 由于实际数据源是有噪的，所以不是所有的对应都有效，这就需要一步一步排除对匹配起负作用的对应
• 从剩下的较好对应中，估计出一个变换

匹配过程中模块

Keypoints（关键点）

关键点是场景中有特殊性质的部分，一本书的边角，书上印的字母P都可以称作关键点。PCL中提供的关键点算法如NARF，SIFT，FAST。你可以选用所有点或者它的子集作为关键点，但需要考虑的是按毎帧有300k点来算，就有300k^2种对应组合。

Feature descriptors（特征描述子）

根据选取的关键点生成特征描述。把有用信息集合在向量里，进行比较。方法有：NARF, FPFH, BRIEF 或SIFT.

Correspondences estimation（对应关系估计）

已知从两个不同的扫描图中抽取的特征向量，找出相关特征，进而找出数据中重叠的部分。根据特征的类型，可以选用不同的方法。

点匹配（point matching， 用xyz坐标作为特征），无论数据有无重组，都有如下方法：

• brute force matching（强制匹配）,
• kd-tree nearest neighbor search (FLANN)（kd树最近邻搜索）,
• searching in the image space of organized data（在图像空间搜索有组织的数据）, 
• searching in the index space of organized data（按索引搜索有组织的数据）.

特征匹配（feature matching， 用特征做为特征），只有下面两种方法：

• brute force matching （强制匹配）
• kd-tree nearest neighbor search (FLANN)（kd树最近邻搜索）.

除了搜索法，还有两种著名对应估计：

• 直接估计对应关系（默认），对点云A中的每一点，搜索在B中的对应关系
• “Reciprocal” 相互对应关系估计，只用A，B重叠部分，先从A到B找对应，再从B到A找对应。

Correspondences rejection（剔除错误估计）

剔除错误估计，可用 RANSAC 算法，或减少数量，只用一部分对应关系。有一种特殊的一到多对应，即模型中一个点对应源中的一堆点。这种情况可以用最短路径对应或检查附近的其他匹配过滤掉。

Transformation estimation（最后一步，计算变换）

• 基于上述匹配评估错误测量值；
• 评估相机不同pose之间所作的刚性变换（运动估计），使错误测量值最小化；
• 优化点云结构；
• E.g, - SVD 运动估计; - Levenberg-Marquardt用不同内核作运动估计；
• 用刚性变换旋转/平移源数据到目标位置，可能需要对所有点/部分点/关键点内部运行ICP迭代循环；
• 迭代，直到满足某些收敛标准。

匹配流程总结