预测数值型数据：回归源码分析（1）

最新推荐文章于 2022-10-21 17:07:35 发布

lilong117194

最新推荐文章于 2022-10-21 17:07:35 发布

阅读量1.5k

点赞数 2

分类专栏：机器学习实战文章标签：线性回归局部加权线性回归预测鲍鱼例子拟合

本文链接：https://blog.csdn.net/lilong117194/article/details/78392261

版权

机器学习实战专栏收录该内容

22 篇文章 2 订阅

订阅专栏

回归模型比较简单，这里先简单介绍下，后面遇到难点再具体分析。

回归的一般方法：
(1)收集数据：采用任意方法收集数据。
(2)准备数据：回归需要数值型数据，标称型数据将被转成二值型数据。
(3)分析数据：绘出数据的可视化二维图将有助于对数据做出理解和分析，在采用缩减法
求得新回归系数之后,可以将新拟合线绘在图上作为对比。
(4)训练算法：找到回归系数。
(5)测试算法：使用幻或者预测值和数据的拟合度，来分析模型的效果。
(6)使用算法：使用回归，可以在给定输入的时候预测出一个数值，这是对分类方法的提
升，因为这样可以预测连续型数据而不仅仅是离散的类别标签。

1. 用简单线性回归找到最佳拟合直线

# -*- coding: utf-8 -*-
"""
Created on Wed Oct 25 16:49:50 2017
"""
from numpy import *
import matplotlib.pyplot as plt


# 数据导入函数
def loadDataSet(fileName):      
    numFeat = len(open(fileName).readline().split('\t')) - 1 # 得到特征数   
    dataMat = []; labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr =[]
        curLine = line.strip().split('\t')
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))
        dataMat.append(lineArr)
        labelMat.append(float(curLine[-1])) # 得到最后一列目标值
    return dataMat,labelMat

# 标准回归函数
def standRegres(xArr,yArr):
    xMat = mat(xArr); yMat = mat(yArr).T
    xTx = xMat.T*xMat # 计算X'X
    if linalg.det(xTx) == 0.0: # 判断xTX行列式是否为0
        print "This matrix is singular, cannot do inverse"
        return
    ws = xTx.I * (xMat.T*yMat)  # 求得当前w的最优估计值
    return ws

# 局部加权线性回归函数
def lwlr(testPoint,xArr,yArr,k=1.0):
    xMat = mat(xArr); yMat = mat(yArr).T
    m = shape(xMat)[0]
    weights = mat(eye((m))) # 产生对角单位权重矩阵
    for j in range(m):                      # 遍历每一个样本点
        diffMat = testPoint - xMat[j,:]     # 所有的数据离测试点的距离
        weights[j,j] = exp(diffMat*diffMat.T/(-2.0*k**2)) # 高斯核得到的权重，并且是对角阵
    xTx = xMat.T * (weights * xMat)
    if linalg.det(xTx) == 0.0:
        print "This matrix is singular, cannot do inverse"
        return
    ws = xTx.I * (xMat.T * (weights * yMat))
    return testPoint * ws

# 为数据集每个点调用lwlr()
def lwlrTest(testArr,xArr,yArr,k=1.0):  # testArr,xArr是同一数据列
    m = shape(testArr)[0] # 得到数据样本的个数
    yHat = zeros(m)       # 0矩阵用于存储预测值
    for i in range(m):    # 
        yHat[i] = lwlr(testArr[i],xArr,yArr,k)
    return yHat


# 主函数

xArr,yArr=loadDataSet('ex0.txt')
ws=standRegres(xArr,yArr) # ws是回归系数
xMat=mat(xArr) # 是前两维的数据
yMat=mat(yArr) # 第三维的数据，就是真实值
yHat=xMat*ws    # 得到预测输出的值yHat
fig=plt.figure()
ax=fig.add_subplot(111)
# xMat[:,1].flatten().A[0]得到xMat第二维的数据，yMat.T[:,0].flatten().A[0]是真实值
ax.scatter(xMat[:,1].flatten().A[0],yMat.T[:,0].flatten().A[0]) # 创建出原始的数据图像
xCopy=xMat.copy() # 拷贝
xCopy.sort(0)  # 升排序
yHat=xCopy*ws  # 得到预测值
ax.plot(xCopy[:,1],yHat,'r')  # 画出拟合直线
plt.show()
# 计算相关系数
yHat=xMat*ws
print 'Correlation coefficient:',corrcoef(yHat.T,yMat) #numpy库提供了相关系数的计算方法

注意：

这里的回归系数是用最小化平方误差得到的，即
$\hat{w}=(X^TX)^{-1}X^Ty$
和代码中的ws = xTx.I * (xMat.T*yMat)相对应。
通过计算两个序列的相关系数，可以计算预测值和真实值之间的匹配程度。Numpy库提供了相关系数的计算方法：通过命令corrcoef（yEstimate,yActual）来计算预测和真实值的相关性。
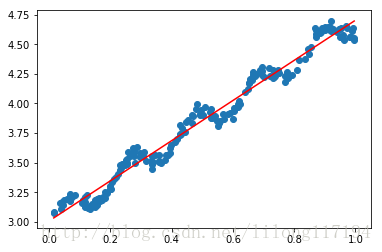
线性回归是得到最佳的回归系数后，再对原始输入样本进行预测，此处的回归系数对于所有的样本都是一样的（yHat=xMat*ws），这点不同于局部线性回归，然后画出原始数据的散点图和回归线。

运行结果：
这里写图片描述

相关系数：

Correlation coefficient: [[ 1.     0.98647356]
                          [ 0.98647356   1.  ]]

2. 局部加权线性回归

线性回归的一个问题是有可能出现欠拟合现象，因为它求的是具有最小均方误差的无偏估计。显而易见，如果模型欠拟合将不能取得最好的预测效果。所以有些方法允许在估计中引人一些偏差，从而降低预测的均方误差。
其中的一个方法是局部加权线性回归（LWLR)。在该算法中，我们给待预测点附近的每个点赋予一定的权重；然后在这个子集上基于最小均方差来进行普通的回归。与KNN一样，这种算法每次预测均需要事先选取出对应的数据子集。该算法解出回归系数 $w$ 的形式如下：
$\hat{w}=(X^TWX)^{-1}X^TWy$
其中 $W$ 是一个矩阵，用来给每个数据点赋予权重。

LWLR使用“核”（与支持向量机中的核类似）来对附近的点赋予更高的权重。最常用的核就是高斯核，高斯核对应的权重如下：
$w(i,j)=exp\left (\frac{|x^i-x|}{-2k^2} \right )$
这样就可以得到要预测的点 $x^{(i)}$ 附近的点的权重值。

把上述的代码中的主函数改为如下：

# 主函数
xArr,yArr=loadDataSet('ex0.txt')
#print 'Weighted prediction:',lwlr(xArr[0],xArr,yArr,1.0)
yHat_1=lwlrTest(xArr,xArr,yArr,1.0)
yHat_2=lwlrTest(xArr,xArr,yArr,0.01)
yHat_3=lwlrTest(xArr,xArr,yArr,0.003)
# 对xArr排序
xMat=mat(xArr) # 转化为矩阵
srtInd=xMat[:,1].argsort(0) # 按升序排列，并返回对应的索引值
xSort=xMat[srtInd][:,0,:]  # 得到二维的矩阵,重新升序后得到的矩阵
#xx=xMat[srtInd]  # 三维的矩阵
fig=plt.figure()
ax=fig.add_subplot(111)
ax.plot(xSort[:,1],yHat_1[srtInd])  # 预测值也按相应的坐标
ax.scatter(xMat[:,1].flatten().A[0], mat(yArr).T.flatten().A[0],s=2,c='r')
plt.show()

fig=plt.figure()
ax=fig.add_subplot(111)
ax.plot(xSort[:,1],yHat_2[srtInd])  # 预测值也按相应的坐标
ax.scatter(xMat[:,1].flatten().A[0], mat(yArr).T.flatten().A[0],s=2,c='r')
plt.show()

fig=plt.figure()
ax=fig.add_subplot(111)
ax.plot(xSort[:,1],yHat_3[srtInd])  # 预测值也按相应的坐标
ax.scatter(xMat[:,1].flatten().A[0], mat(yArr).T.flatten().A[0],s=2,c='r')
plt.show()

运行结果：
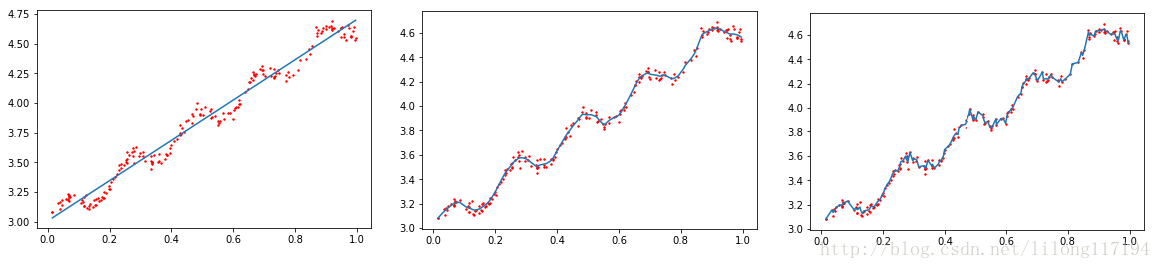
这里写图片描述
可以看到从左到右的系数k分别为：1.0，0.01，0.003 的拟合效果。
参数k决定了对待测点附近的点赋予多大的权重，控制着权重衰减的速度。

分析：
其中待预测点附近点的权重的代码：

for j in range(m):                      # 遍历每一个样本点
        diffMat = testPoint - xMat[j,:]     # 所有的数据离测试点的距离
        weights[j,j] = exp(diffMat*diffMat.T/(-2.0*k**2)) # 高斯核得到的权重，并且是对角阵

diffMat*diffMat.T：是每个待测点与样本的每个点的距离。
weights：是基于每个待测点与全部样本点进行计算得到的权重对角阵。
return testPoint * ws ：返回待测点的预测值，而每个待测点的权重都要基于全部样本进行计算。
ax.plot(xSort[:,1],yHat_1[srtInd]) ：画出回归线
ax.scatter(xMat[:,1].flatten().A[0], mat(yArr).T.flatten().A[0],s=2,c='r')：画出原始数据的散点图。

要注意的语法：

srtInd=xMat[:,1].argsort(0) # 按升序排列，并返回对应的索引值
xx=xMat[srtInd]  # 三维的矩阵
xSort=xMat[srtInd][:,0,:]  # 得到二维的矩阵,重新升序后得到的矩阵

xMat[索引值][:,0,；]其得到的是：二维的矩阵，而xMat[索引值]得到的是三维的形式，效果如下：

In [21]: xSort
Out[21]: 
matrix([[ 1.      ,  0.014855],
        [ 1.      ,  0.015371],
        [ 1.      ,  0.033859],
        ..., 
        [ 1.      ,  0.990947],
        [ 1.      ,  0.993888],
        [ 1.      ,  0.995731]])

In [22]: xx
Out[22]: 
matrix([[[ 1.      ,  0.014855]],

        [[ 1.      ,  0.015371]],

        [[ 1.      ,  0.033859]],

        ..., 
        [[ 1.      ,  0.990947]],

        [[ 1.      ,  0.993888]],

        [[ 1.      ,  0.995731]]])

In [23]: shape(xx)
Out[23]: (200L, 1L, 2L)

In [24]: shape(xSort)
Out[24]: (200L, 2L)

In [25]:

3. 预测鲍鱼的年龄

添加计算误差大小的函数，并改变主函数如下：

# 计算预测误差的大小
def rssError(yArr,yHatArr): # yArr和yHatArr都需要是数组
    return ((yArr-yHatArr)**2).sum()

# 主函数

abX,abY=loadDataSet('abalone.txt')
yHat01=lwlrTest(abX[0:99],abX[0:99],abY[0:99],0.1) 
yHat1=lwlrTest(abX[0:99],abX[0:99],abY[0:99],1)
yHat10=lwlrTest(abX[0:99],abX[0:99],abY[0:99],10)
print 'k=0.1 :',rssError(abY[0:99],yHat01.T)  # 不同的核的预测预测误差结果
print 'k=1 :',rssError(abY[0:99],yHat1.T)
print 'k=10 :',rssError(abY[0:99],yHat10.T)
# 测试新数据的表现
print 'Forecast new data....'
yHat01=lwlrTest(abX[100:199],abX[0:99],abY[0:99],0.1) # 此处的权重计算是基于前100个样本的，但预测的是另100个
yHat1=lwlrTest(abX[100:199],abX[0:99],abY[0:99],1)
yHat10=lwlrTest(abX[100:199],abX[0:99],abY[0:99],10)
print 'k=0.1 :',rssError(abY[100:199],yHat01.T)
print 'k=1 :',rssError(abY[100:199],yHat1.T)
print 'k=10 :',rssError(abY[100:199],yHat10.T)
# 和简单的线性回归对比
print 'compare to Simple regression:....'
ws=standRegres(abX[0:99],abY[0:99])
yHat=mat(abX[100:199])*ws
print 'Simple regression:',rssError(abY[100:199],yHat.T.A)

运行结果：

k=0.1 : 56.7836322443
k=1 : 429.89056187
k=10 : 549.118170883
Forecast new data....
k=0.1 : 14651.309989
k=1 : 573.52614419
k=10 : 517.571190538
compare to Simple regression....
Simple regression: 518.636315325

分析：

使用较小的核将得到较低的误差。那么,为什么不在所有数据集上都使用最小的核呢？这是因为使用最小的核将造成过拟合，对新数据不一定能达到最好的预测效果
简单线性回归达到了与局部加权线性回归类似的效果。这也表明一点，必须在未知数据上比较效果才能选取到最佳模型。那么最佳的核大小是10吗？或许是，但如果想得到更好的效果，应该用10个不同的样本集做10次测试来比较结果。
预测鲍鱼的年龄的例子展示了如何使用局部加权线性回归来构建模型，可以得到比普通线性回归更好的效果。局部加权线性回归的问题在于，每次必须在整个数据集上运行。也就是说为了做出预测，必须保存所有的训练数据。这是其劣势所在。

lilong117194

关注

2
点赞
踩
3

收藏

觉得还不错? 一键收藏
0
评论
预测数值型数据：回归源码分析（1）

回归模型比较简单，这里先简单介绍下，后面遇到难点再具体分析。回归的一般方法： (1)收集数据：采用任意方法收集数据。 (2)准备数据：回归需要数值型数据，标称型数据将被转成二值型数据。 (3)分析数据：绘出数据的可视化二维图将有助于对数据做出理解和分析，在采用缩减法求得新回归系数之后,可以将新拟合线绘在图上作为对比。 (4)训练算法：找到回归系数。 (5)测试算法：使用幻或者预测值和数
复制链接

扫一扫