本文为斯坦福大学吴恩达教授的《机器学习》视频课程第三章主要知识点。
分类问题举例
邮件:垃圾邮件/非垃圾邮件?
在线交易:是否欺诈(是/否)?
肿瘤:恶性/良性?
以上问题可以称之为二分类问题,可以用如下形式定义:
其中0称之为负例,1称之为正例。
当y值只有1或0两个值时,如果还使用线性回归,会因为x的样例增加而改变线性回归方程,所以线性回归不适用。
分类问题的假设函数
因为假设函数 0≤hθ(x)≤1,所以我们使用逻辑回归方程来实现
函数g(z)的图形示意如下:
函数值处于0-1之间
hθ(x)能告诉我们输入为x时,函数值为1的概率,比如hθ(x)=0.7 表示,函数值为1的概率为70%。
同样,根据以下公式:
可以知道函数值为0的概率为:
P(y=0|x; θ) = 1-P(y=1|x; θ) = 1-0.7 = 0.3
决策边界
为了实现假设函数输出0或1这两种分类,需要将假设函数的值转化为0或1,即:
那对于逻辑回归方程,想要输出值大于0.5,则输入值z需要大于0.
当输入值z为θTX时,则意味着θTX≥0,即
区分y值为0或者1的边界就是决策边界,可以根据相应的参数θ,算出各个特征变量x之间的关系。
例如:
注:决策边界由假设函数的θ 决定
代价函数
在逻辑回归中,若想获取代价函数的最优解,我们不能使用线性回归中的代价函数方程作为逻辑回归的代价函数,因为这样画出来的代价函数图像是波浪状的,会有很多的局部最优解,从而不能判断哪一个是最终最优解。
所以,我们根据y的值(0或1),将逻辑回归的代价函数某一部分写成以下形式:
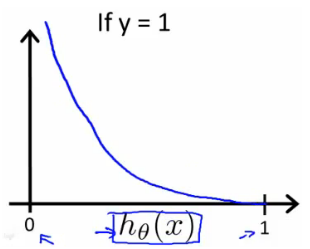
当y为1时,得到J(θ) 与 hθ(x)之间的关系图为:
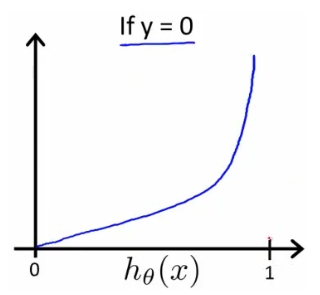
当y为0时,得到J(θ) 与 hθ(x)之间的关系图为:
写成函数表达式就是:
在逻辑回归中,将代价函数写成上述形式,能够保证代价函数与逻辑回归函数的图像是凸形的。
因为y的值要么是0,要么是1,所以我们可以将代价函数的某一部分改写成:
完整的代价函数写成:
一般梯度降低方法的公式为:
具体带入,则为:
同时更新所有的θ,直到代价函数与调试次数的函数收敛到一定程度。
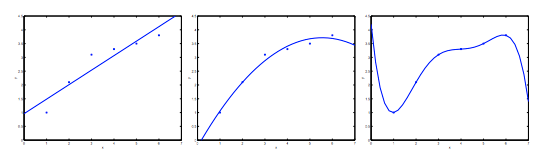
关于过拟合
从图中的三幅图可以看出,左边的拟合函数过于简单,没有完全捕捉信息,有高偏差,属于欠拟合;
中间的图较好的拟合了样本数据;
而右边图中的曲线很好的穿过了所有的样本,但函数变量过多,曲线过于扭曲,不能很好的泛化到新的样本数据中,属于过拟合。
过拟合现象在线性回归和逻辑回归中都可能出现,主要有两种方法避免过拟合问题:
1、减少特征向量的数量
- 手动挑选保留的特征向量
- 使用挑选模型算法
2、正则化
保留所有的特征向量,但是减小参数的θ的大小
当所有的参数θ减小时,假设函数就会变得相对平滑一些,就比较容易避免过拟合现象。
正则化线性回归
正则化线性回归帮助线性回归方程避免过拟合(即使训练样本小&特征向量多),还可以帮助解决XTX不可逆的问题。
在梯度下降方法中,对参数θ的调试过程中,从θ1开始(而不是θ0),给每一个参数加上一个正则项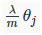
经过变换,我们的梯度下降方法可以写成:
其中肯定是小于1的,所以经过每一次调试,θj都会变小
除了梯度下降法,在正规方程中,也能使用正则化线性回归:
矩阵L是对角线上第一个数为0,其他都为1 ,剩下的部分都为0的矩阵,维度是(n+1)×(n+1)。若XTX不可逆,λ⋅L的加入也可以帮助解决XTX不可逆的问题。
逻辑回归函数的正则化:
对逻辑回归函数进行正则化,也是在代价函数的后面加上一个正则项,解决复杂的非线性分类问题:









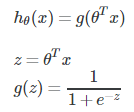

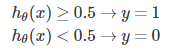
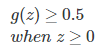
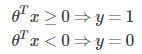
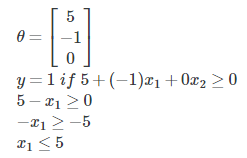
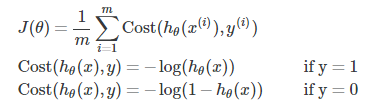
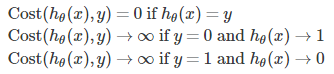
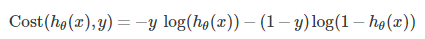
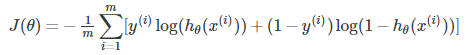
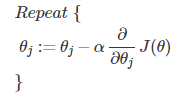
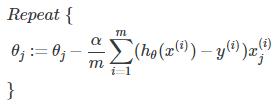
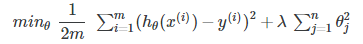
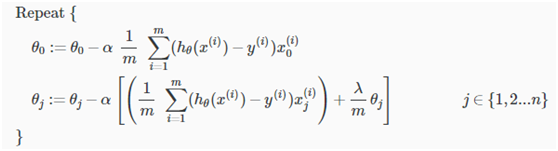
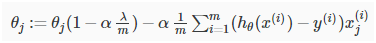
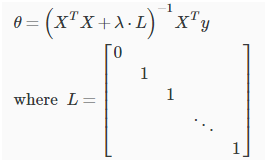
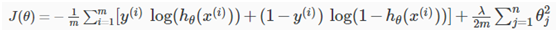














 762
762

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








