基数、尾数、阶码、精度、范围、规格化、单精度浮点数（（32bit）、双精度浮点数（（64bit）、IEEE754 讲解

        在本个内容中我们会进行基数、尾数、阶码、精度、范围、规格化、单精度浮点数（（32bit）、双精度浮点数（（64bit）、IEEE754 讲解的相关内容讲解，本文参考于吴迪副教授的资料，浙江大学，华中科技大学课程所著

一、定点表示

        既然需要引入浮点数，那么更多的问题是：

        浮点数能够模拟数轴上连续的小数吗？精度？

        浮点表示的格式是什么？

        尾数和阶码的基值必须是 2 吗？基值的影响？

        数的范围与精度和哪些因素有关？

        为什么要引入规格化表示?

        目前浮点数表示格式的标准是什么？

（复习内容）回忆定点数：下面，公式要写在笔记上，用作后面举例计算【浮点数精度】的讲解依据

二、浮点表示的定义和范围

CLAIM（1：基数为 2 时，数位右/左移几位，阶码就加/减几；反过来也一样。）

以下内容要抄在笔记上，随时查看。

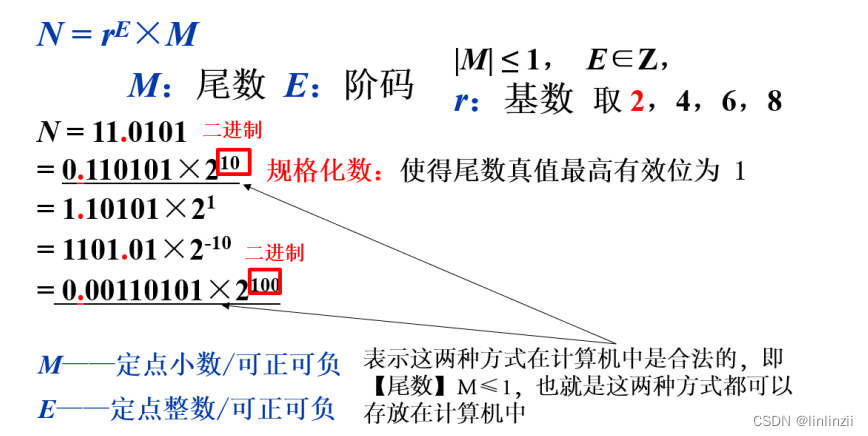
        阶码——其位数决定数据表示的范围，阶码的位数越多，能表示的数据范围也就越大；而阶码的 值和阶符共同决定了小数点的位置（注意对照观察右边的具体例子）

        尾数——尾数的尾数决定了数据表示的精度（数轴上的最小刻度）。阶码长度相同的时候，分配 给尾数的数位越多，数据的精度就越高。

         注意：E 为定点整数，M 为定点小数。我们之前学过的定点数的表示方法，在这里得到了应用。

         这里的【浮点数格式框图】要画在黑板上，用作后面举例计算【浮点数精度】的讲解依据

E——阶码部分，假设用 4 位数位(k=4)表示，一共是 5 位，还有 1 位符号位

M——尾数部分，设用 10 位数位(n=10)表示，一共 11 位，其中 1 位是符号位

        这样，一共便是 16 位，我们的机器假设就是 16 位的机器，一共能表示的二进制数的个数就是 2 16 个，如果我们的机器用这个格式来表示浮点数的话，也就是用 2 16 个数来表示最小负数和最大正数之 间的所有的数。而 2 16也就是 6 万多个数，实际上是用有限的数据，来表示无限的实数。

        根据【笔记上画的浮点数框图、和浮点数公式】，我们来计算最小、最大负数；对于最小、最大 正数的计算，大家自行思考。（【注意：这里所有的计算是用原码表示的】（（如果是补码表示 的，可以根据补码的公式得到） 

      

问 1：在 k=4,n=10 时，浮点数的精度是多少？正数的范围是从多少到多少？

        答：精度（最小刻度）：0.00（0000（0001； 范围：正数从 0.00（0000（0001×2 -15→0.11（ 1111（1111×2 15，最小数接近 0，最大的数接近 32768。

问 2：从 0.00（0000（0001×)到 0.11（1111（1111×)，一共有多少个数？

        答： -1 个

问 3：一共有多少个正数？（原码）

        答：阶码从-15→+15 共 31 个，每个阶码对应了（-1）个尾数，31×（ -1）≈31000 个。

CLAIM 3： 浮点数的精度和尾数的位数有关，尾数的位数越多，精度越高；

                   浮点数的范围与阶码的位数有关，阶码的位数越多，范围越大。

上溢出时：浮点运算器的溢出标记位设置为 1。

下溢出 时：由于绝对值很小，则按照机器 0 处理。

精度溢出：浮点数确实在“正数区”和“负数区”，但是不在某个刻度上的时候，此时只能做（“ 舍入”（（近似数）处理。比如：0.00 0000 1101 101×，在 0.00 0000 1101×2 -9 与 0.00 0000 1110×之间。 

三、浮点表示的规格化

四、IEEE（754 标准

为什么需要浮点数表示的标准？

        答：虽然我们定义了浮点数的存储方式，优化了浮点数的存储（规格化），但是浮点数的一般格 式没有规定①数的位数②机器码的形式：原、补、反？所以，如果看成不同的机器码，则对应的真值 都不同，便不是一个数。

        IEEE754 规定：阶码用移码表示。为什么要采用移码？这主要是为了让阶码的值成为非负，便于 浮点数的比较和排序。让我们复习移码，查看【移码的表格】

        对于单精度浮点数，本来的阶码 E： 1，1111111→0，1111111 即：-127→+127

        为了方便，使得阶码最低位等于 0，所以需要+127（偏移量）：

         现在+127 移码后：0→+254， 即：现在的 E（移码）0→254。

         规格化的方式：最高位为“1”是隐含的：即（【尾数】的第一位固定为 1，那么，我们就可以少 存储一位，即【隐含】掉，也就是说，表示的时候不表示（存储的时候不存储），计算的时候补上它 就可以了，这样的话，实际上是增加了尾数，从而增加了数据表示的精度。 

        另外，需要指出的是：与之前的浮点表示类似，规格化浮点数在数轴上的刻度分布不是均匀的， 因为同样的道理，指数每加 1，数的数值就扩大为原来的 2 倍，而此范围内包含的数的个数与扩大之 前是一样的，所以，刻度只会越来越稀疏。

CLAIM 4： 偏移量越大，则规格化数的范围越小、非规格化数的精度越高。

 

 

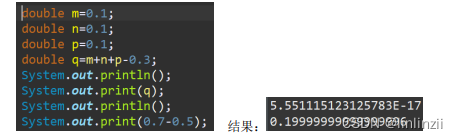
        我们要认识到，这样的误差会导致严重的后果，特别是那些对误差极其敏感的情况（火箭发射、 金融计算），好在 2008 年 IEEE 754 标准进行了修订，引入了十进制浮点数——DFP 编码，

        最后，我们来学习一个例子。