线性代数——行列式

行列式的性质

1. 行列式与它的转置行列式相等

2. 对换行列式的两行（列），行列式变号

推论：如果行列式有两行（列）完全相同，则此行列式等于0

证：把这两行兑换，有D=-D,故此行列式等于0

3. 行列式的某一行（列）中所有的元素都乘同一数，等于用数k乘此行列式

推论：行列式中某一行（列）的所有元素的公因子可以提到行列式记号的外面

4.行列式中如果有两行（列）元素成比例，则此行列式等于0

性质4 由下面2个性质推理得到：

性质3 行列式的某一行（列）中所有的元素都乘同一数，等于用数k乘此行列式

如：第一行/第二行=2，第二行*2=第一行，两行相同，则此行列式等于0

推论 如果行列式有两行（列）完全相同，则此行列式等于0

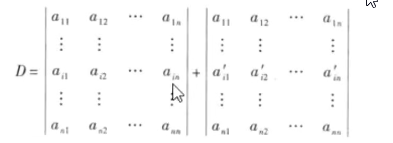
5.若行列式的某一行（列）的元素都是两数之和，例如第i行的元素都是两数之和

则D等于下列两个行列式之和：