无信息搜索（上）

无信息搜索是指除了问题定义中提供的状态信息外没有任何附加信息。

特点：

1. 算法只能区分状态是不是目标状态；
2. 无法比较非目标状态的好坏。

策略：

1. 宽度优先搜索
2. 一致代价搜索
3. 深度优先搜索
4. 深度受限搜索
5. 迭代加深的深度优先搜索

 

一、宽度优先搜索

1.基本思想：

宽度优先搜索是简单搜索策略，先扩展根结点，接着扩展根结点的所有后继，然后再扩展它们的后继，依次类推。一般地，在下一层的任何结点扩展之前，搜索树上本层深度的所有结点都应该已经扩展过。

       宽度优先搜索是一般图搜索算法，每次总是扩展深度最浅的结点，这可以通过将边缘组织成FIFO队列来实现。

2.图例示意：

一颗简单二叉树上的宽度优先搜索，利用一个记号指出下一个将要扩展的结点。

 

3.伪代码：

（1）算法实现思想：

a.选中第一个被访问的顶点；

b.对顶点作已访问过的标志；

c.依次访问已访问顶点的第1,2，……个未被访问过的邻接顶点，并进行标记；转向（c）；

d.如果还有顶点未被访问，则选中一个起始顶点，转向（b）；

e.所有顶点都被访问到，则结束。

 

（2）伪代码：

4.属性：

（1）完备性：宽度优先算法答案是完备的；

（2）时间复杂度：；

（3）空间复杂度：；

（4）内存需求大；

（5）时间复杂度高。

二、一致代价搜索

1.基本思想

       一致代价搜索扩展的路径是消耗g(n)最小的结点n。

       在这里我们按照路径代价对队列进行排序，同时在入队列时进行检测，因为第一个生成的目标结点可能在次游路径上。

2.图例示意

       从Sibiu到Bucharest：

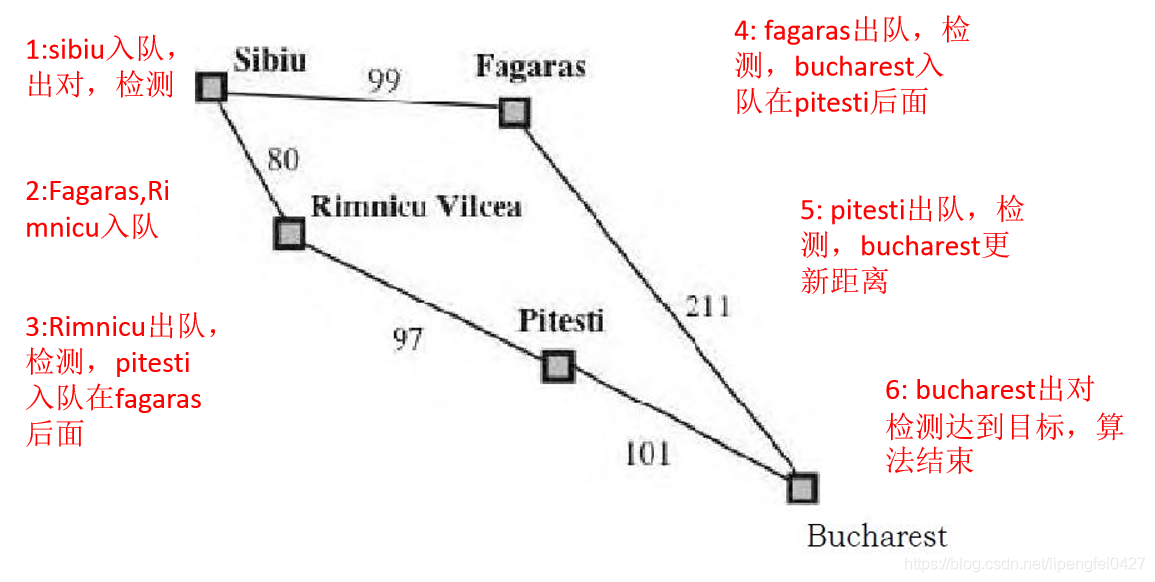
3.伪代码

 

4.属性

（1）一致代价搜索对路径的步数并不关心，只关心路径总代价。如果每一步的代价都大于等于某个小的正值常数a,则一致代价搜索是完备的，也就是说一致代价搜索不具有完备性。

（2）时间复杂度

（3）空间复杂度

因为一致代价搜索在探索包含代价大的行动之前，经常会探索代价小的行动步骤所在的很大的搜索树，所以一致代价搜索可能会多很多无意义的工作。宽度优先搜索和一致代价搜索都是基于扩展深度最浅的未扩展结点进行的。接下来就是扩展搜索树的当前边缘结点集中最深的结点。详见下！