学期projet总结:
当把点的数据和线的数据读进来之后,为了画出地图还有最重要的一步就是把实际的经纬度转换成屏幕像素点的坐标。在找老师讨论之前,我在网上查资料,找到了下边链接的文章,并按照这个方法画出了地图。
相关文章链接
1月4号,新年后第一天上课,我去找导师让他看做出来的软件的效果,画出来的地图明显和他的不一样,他就把他的方法分享了。
他的方法的主要思路就是找到一个城市所有点里面经度和纬度最小的点作为坐标原点,然后求其他点到这个点的距离,这个距离是地理空间的实际距离,并以此算出坐标。因为屏幕的坐标原点在左上方,所有我计算的步骤如下
- 以经度最小值和纬度最大值作为坐标原点(minLongitude,maxLatitude)
- 求其他点到坐标原点的距离(实际地理空间距离),找出最大距离maxDistance
- 获取屏幕宽度和高度,求出斜对角线的长度,勾股定理
- 算出最大距离与屏幕斜对角线的比值,再乘以2作为换算比率,ratio
- 求出每个点相对于原点的x,y轴的距离,除以换算比率得到屏幕坐标
第2步,求两点间的实际地理空间距离,导师提供了一个算法,这个方法是把地球当成一个球面模型
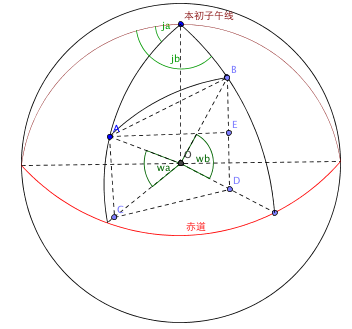
假设地图上有A(ja,wa),B(jb,wb)两点,ja,wa是A点的经纬度,jb,wb是B点的经纬度。A和B两点的球面距离就是AB的弧长,AB弧长=地球半径*角AOB,O是地球球心。计算公式如下:
代码如下:
public static double distanceLongLat(double longitudeA, double longitudeB,
double latitudeA, double latitudeB) {
double longA = longitudeA * Math.PI / 180;
double longB = longitudeB * Math.PI / 180;
double latA = latitudeA * Math.PI / 180;
double latB = latitudeB * Math.PI / 180;
double deltaLong = longB - longA;
//角AOB
double radianAB = Math.acos(Math.sin(latA) * Math.sin(latB)
+ Math.cos(latA) * Math.cos(latB) * Math.cos(deltaLong));
//AB弧长
return (radianAB * 6378000);
}获取屏幕宽和高的代码如下:
//获得屏幕大小
Dimension screensize = Toolkit.getDefaultToolkit().getScreenSize();
int screenWidth = (int)screensize.getWidth();
int screenHeight = (int)screensize.getHeight();求距离坐标原点最远的点,求出换算比率。代码如下:
//求距离参照点最远的点
double maxDistance = distanceLongLat(minLongitude, ReadFile.longitude.get(0),
maxLatitude, ReadFile.latitude.get(0));
for (int i = 0; i < ReadFile.longitude.size(); i++){
maxDistance=Math.max(maxDistance,distanceLongLat(minLongitude,
ReadFile.longitude.get(i), maxLatitude, ReadFile.latitude.get(i)));
}
//转换比率
double ratio = 2*maxDistance / Math.sqrt((screenWidth * screenWidth
+ screenHeight * screenHeight));将所有点的经纬度转换成屏幕像素坐标,并将转换后的坐标用一个ArrayList保存。代码如下:
public static ArrayList<Point> point = new ArrayList<Point>();
//将经纬度转换成屏幕坐标
for (int i = 0; i < ReadFile.longitude.size(); i++) {
Point p = new Point();
p.x = (int) (distanceLongLat(minLongitude,
ReadFile.longitude.get(i), maxLatitude, maxLatitude) / ratio);
p.y = (int) (distanceLongLat(minLongitude, minLongitude,
maxLatitude, ReadFile.latitude.get(i)) / ratio);
point.add(p);
}用point里保存的坐标就可以画地图了。画出来巴黎的地图如下:
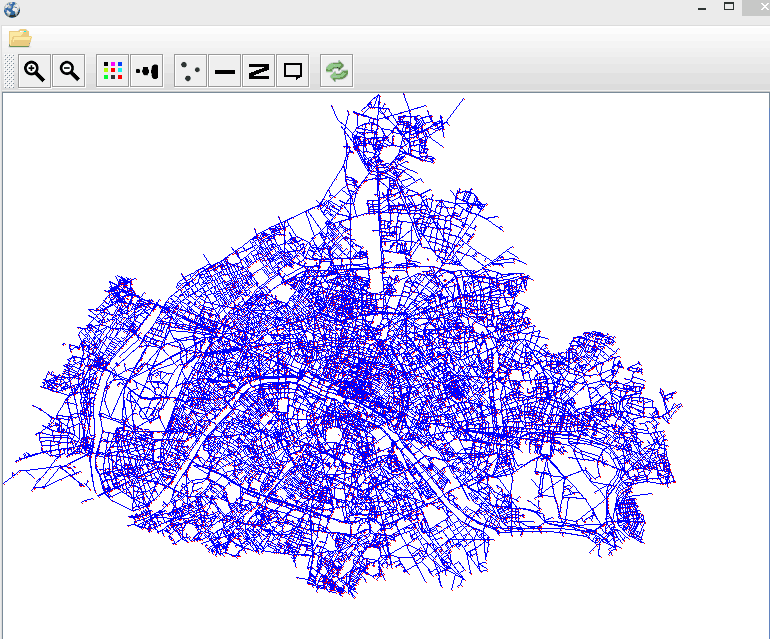
在最后一步,把每个点的经纬度转换成屏幕坐标时,原理如下图:
O点是屏幕左上角,坐标原点,求B点的X,Y值,OB1的距离为X轴的值,OB2 的距离为Y轴的距离,然后再除以换算比率(ratio)适应屏幕大小。
以该方法画地图时,当点很多时,画的很慢。例如画旧金山时,点的数量达到了175000个!!!!而巴黎的数据,点的数量是29000个,柏林的点是60000个。所以画旧金山用时在7.5秒左右。然后我读到了美团网的一篇技术文章,链接如下
地理空间距离计算优化
用该文章介绍的“简化距离计算公式方法“,在画旧金山时可以提高到5.5秒左右。
我分析了一下,我的程序里有三个地方用到了求两点距离的代码,一是求最远距离,另外是求X,Y坐标,这三次计算都要算17.5W次,计算公式里面还有一个三角函数。美团网计算用户到商家的距离只计算一次。
该部分完整代码如下:
import java.awt.Dimension;
import java.awt.Point;
import java.awt.Toolkit;
import java.util.ArrayList;
import com.vg.io.ReadFile;
/**
* 将经纬度转换成屏幕像素坐标
*
*/
public class LocationTransfer {
public static ArrayList<Point> point = new ArrayList<Point>();
public static double minLongitude = ReadFile.longitude.get(0);
public static double maxLatitude = ReadFile.latitude.get(0);
// change longitute and latitude to view point
public static void makeScreenPoint(String fileName) {
for (int i = 0; i < ReadFile.longitude.size(); i++) {
minLongitude = Math.min(minLongitude, ReadFile.longitude.get(i));
maxLatitude = Math.max(maxLatitude, ReadFile.latitude.get(i));
}
/************************************************************/
//获得屏幕大小
Dimension screensize = Toolkit.getDefaultToolkit().getScreenSize();
int screenWidth = (int)screensize.getWidth();
int screenHeight = (int)screensize.getHeight();
//求距离参照点最远的点
double maxDistance = distanceLongLat(minLongitude, ReadFile.longitude.get(0),
maxLatitude, ReadFile.latitude.get(0));
for (int i = 0; i < ReadFile.longitude.size(); i++) {
maxDistance = Math.max(maxDistance, distanceLongLat(minLongitude,
ReadFile.longitude.get(i), maxLatitude, ReadFile.latitude.get(i)));
}
//转换比率
double ratio = 2*maxDistance / Math.sqrt((screenWidth * screenWidth
+ screenHeight * screenHeight));
//将经纬度转换成屏幕坐标
for (int i = 0; i < ReadFile.longitude.size(); i++) {
Point p = new Point();
p.x = (int) (distanceLongLat(minLongitude,
ReadFile.longitude.get(i), maxLatitude, maxLatitude) / ratio);
p.y = (int) (distanceLongLat(minLongitude, minLongitude,
maxLatitude, ReadFile.latitude.get(i)) / ratio);
point.add(p);
}
}
//简化距离公式法
public static double distanceLongLat( double lng1,double lng2,double lat1,
double lat2) {
double dx = lng1 - lng2; // 经度差值
double dy = lat1 - lat2; // 纬度差值
double b = (lat1 + lat2) / 2.0; // 平均纬度
double Lx = dx * Math.PI/180 * 6367000.0 * Math.cos(b*Math.PI/180); // 东西距离
double Ly = 6367000.0 * dy*Math.PI/180; // 南北距离
return Math.sqrt(Lx * Lx + Ly * Ly); // 用平面的矩形对角距离公式计算总距离
}
}






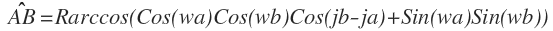














 2921
2921

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








