模式分类--贝叶斯决策论2

前面章节介绍了贝叶斯决策论，现在我们将其推广到多个特征、多种状态类别、更一般的损失函数行为。
首先特征标量x变为特征向量x,如果有d个特征，则称其d维欧几里得空间为特征空间（二维的欧几里得空间就是一个平面直角坐标系，三维就是一个立体）。
行为是指给定x，我们将其划分为类别w或者拒绝决策等等。

最小化条件风险

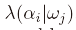
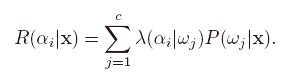
我们有一个观测特征x，我们要采取某一行动，这些行动是有风险（损失、代价）的。用 来表示。那么给定x，我们可能带来的损失期望（条件风险）可以用下式表示：

该式的含义是，在x的条件下，我们将其分类为不同状态w时（概率），我们对风险的预期（联系一下期望的运算公式很容易理解）。
这样，不管我们遇到什么样的x，我们只要通过选择最小化条件风险的行为，预期风险达到最低，将后验概率与代价函数联系到一起。
总风险依然是一个期望（寻找规则使其最小化）：