模式分类--贝叶斯决策论--引言

引言

贝叶斯决策论从概率角度分析不同分类决策以及决策代价之间定量折中。

   通俗点讲，把分类问题看做是概率问题，从已知的样本集中，估计一些概率值，进而估计下一次出现某个预测样本时（条件），样本属于某一类别（随机变量）的概率（后验概率）。寻找判别函数，假如决策代价相同，那么判别函数为后验概率大的类别作为预测类别。

贝叶斯公式推导过程：
联合概率密度公式：

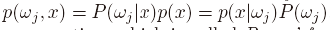
整理后得到贝叶斯公式：

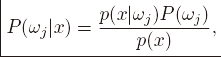
分母计算方法：

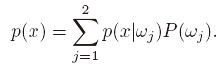
贝叶斯公式各部分含义：

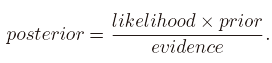
这里明确几个概念，什么是先验概率、后验概率、似然函数、证据，以鲑鱼和鲈鱼为例。
先验概率prior：我们拿到待预测样本之前，我们知道的内容，可以作为先验知识，例如我们已知鲑鱼和鲈鱼出现的概率分别为0.3和0.7。这些概率可以通过训练样本获得（100个样本中有30条是鲑鱼，70条是鲈鱼，那么我们可以估计），因为我们假设训练样本是从某一分布中随机抽取的，训练样本应该与总体就有相同分布。
后验概率posterior：我们拿到待预测样本后，该样本属于某一类别的概率（未知，需要通过贝叶斯公式计算的量）。
似然函数likelihood：每一个特征（随机变量用x表示），在不同的类别（w表示）下具有不同的分布（概率密度函数），就是说在类别w为鲈鱼时，x大概是什么样子。这样，我们有了x和先验知识就可以估计w。
证据：证据的作用是使后验概率的和为1。

误差概率：当类别为鲈鱼时，我们选择为鲑鱼的概率，或者相反的概率。

另一种表述方法：

平均误差也就是误差概率的期望：

贝叶斯决策论可以选择最大后验概率作为判别函数，也可以选择最小误差概率作为判别函数，在误判代价相同的情况下，二者是一样的。

至此，我们已经了解贝叶斯决策中的相关概念。完整的分类过程如下：通过训练样本（参数估计或者非参估计），我们估计在类别分别为鲈鱼和鲑鱼时似然函数的概率密度函数（形式已知或者未知）；一般假设先验概率相同（也可以根据其他方式获得先验概率）；进而根据贝叶斯规则得到后验概率，通过后验概率建立合适的判别函数，最终获得新样本的类别。