导数定义:
求导是数学计算中的一个计算方法,它的定义就是,当自变量的增量趋于零时,因变量的增量与自变量的增量之商的极限。在一个函数存在导数时,称这个函数可导或者可微分。可导的函数一定连续。不连续的函数一定不可导。
定义(导数):设函数 y=f(x) 在点 x0 的某邻域内有定义,若极限
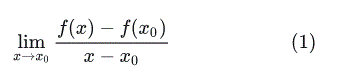
存在,则称函数 f 在点 x0 可导,并称该极限为函数 f 在点 x0 的导数,记作 f′(x0)
注:令 x=x0+Δx , Δy=f(x0+Δx)−f(x0) ,则上述可改写为
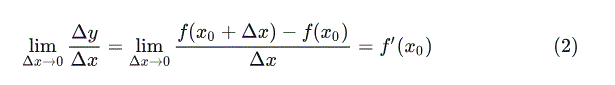
,所以导数是函数增量 Δy 与自变量之比 Δy/Δx 的极限. 这个增量比称为函数关于自变量的平均变化率(又称差商),而导数 f′(x0) 则为 f 在 x0 处关于 x 的变化率
几何上,导数对应函数图像在某一点处切线的斜率。
在物理中,导数可表示瞬时变化率。
导数公式:
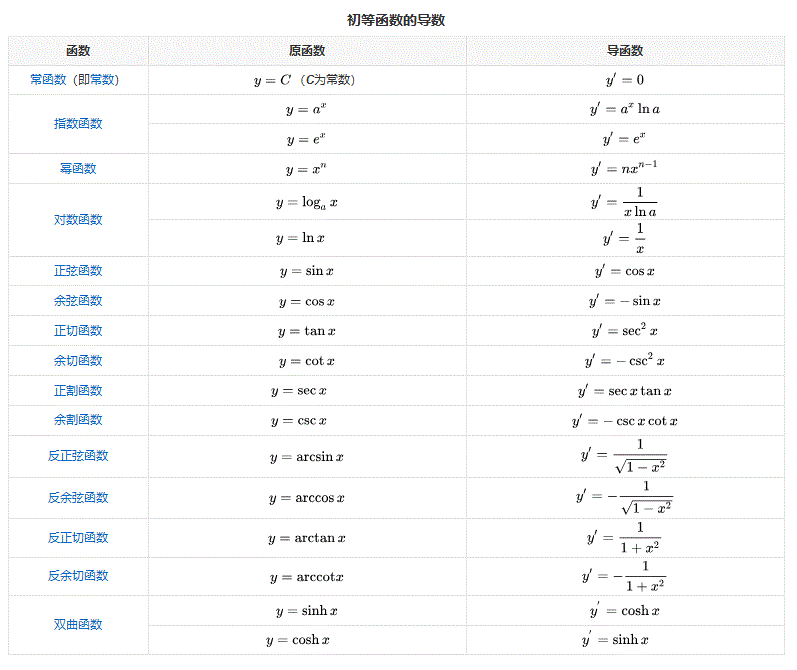





积分:
积分是微积分学与数学分析里的一个核心概念。通常分为定积分和不定积分两种。直观地说,对于一个给定的正实值函数,在一个实数区间上的定积分可以理解为在坐标平面上,由曲线、直线以及轴围成的曲边梯形的面积值(一种确定的实数值)。
积分公式:
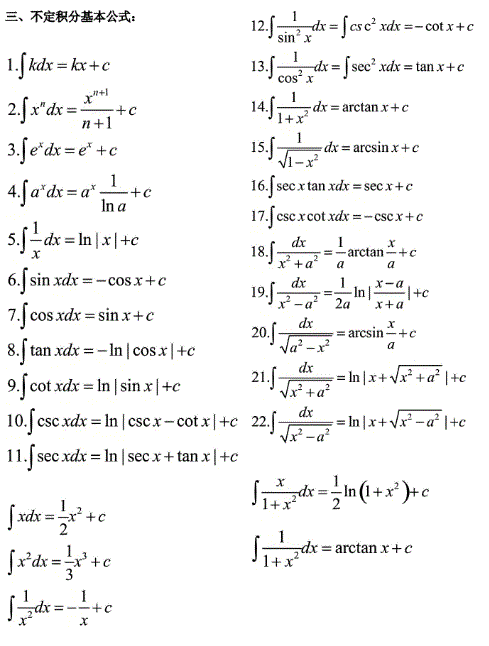





























 7024
7024

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










