线性代数几种特殊类型行列式_及其计算

文章目录:

1、箭形（爪形）行列式（上(下)三角形）【重复】

2、两三角型行列式（爪形、拆行(列)法、化为两三角型、升阶法 ）

2.1 对这类行列式，当b=c时可以化为上面列举的爪形来计算，当b不等于c时则用拆行(列)法来计算

2.2 通过适当变换可以化为两三角型行列式的

2.3 一些每行上有公因子但是无法向上式那样在保持行列式不变得基础上能提出公因子的，采用升阶法 

3、两条线型行列式（直接展开降阶）

4、Hessenberg型行列式（累加消点法）

5、三对角型行列式（递推法(特征方程法)）【重复】

6、各行(列)元素和相等的行列式（提取公因式后）【重复】

7、相邻两行(列)对应元素相差K倍型的行列式（逐步作差的方法）

8、范德蒙德型行列式（范德蒙德行列式）【重复】

---

点我跳转 线性代数常见的几种行列式 

刚刚开始学习线性代数的同学们，有没有被行列式搞得有些头昏脑涨了，别怕！几种特殊类型行列式及其计算来了，想不想了解都有哪几种特殊类型行列式，这些特殊类型行列式又该如何计算，那还等什么，快来看看吧！

拆行法
升阶法
方程组法
累加消点法
累加法
递推法（特征方程法）
步步差法

---

1、箭形（爪形）行列式（上(下)三角形）【重复】

这类行列式的特征是除了第行(列)或第行(列)及主(次)对角线上元素外的其他元素均为零

对这类行列式可以直接利用行列式性质将其化为上(下)三角形行列式来计算.

即利用对角元素或次对角元素将一条边消为零

---

2、两三角型行列式（爪形、拆行(列)法、化为两三角型、升阶法 ）

这类行列式的特征是对角线上方的元素都是c,对角线下方的元素都是b的行列式

初看，这一类型似乎并不具普遍性，但很多行列式均是由这类行列式变换而来

2.1 对这类行列式，当b=c时可以化为上面列举的爪形来计算，当b不等于c时则用拆行(列)法来计算

 前面的几列都减去最后一列

 

2.2 通过适当变换可以化为两三角型行列式的

2.3 一些每行上有公因子但是无法向上式那样在保持行列式不变得基础上能提出公因子的，采用升阶法 

 加边升阶 

---

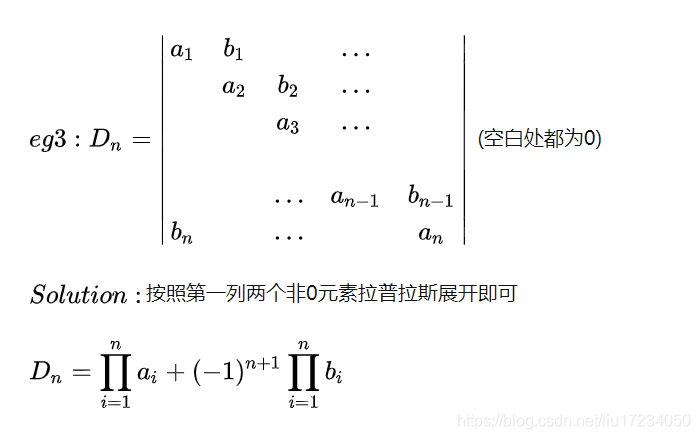
3、两条线型行列式（直接展开降阶）

这类行列式的特征是除了主(次)对角线或与其相邻的一条斜线所组成的任两条线加四个顶点中的某个点外，其他元素都为零

这类行列式可直接展开降阶，对两条线中某一条线元素全为的，自然也直接展开降阶计算

---

4、Hessenberg型行列式（累加消点法）

这类行列式的特征是除主(次)对角线及与其相邻的斜线，再加上第一行(列)或第n行(列)外，其他元素均为零

这类行列式都用累加消点法，即通常将第一行(列)元素化简到只有一个非零元素，以便于这一行或列的展开降阶计算

---

5、三对角型行列式（递推法(特征方程法)）【重复】

这是一种递推结构的行列式，特征为所有主子式都有相同的结构，从而以最后一列展开，将所得的(n-1)  阶行列式再展开即得递推公式，即递推法(特征方程法)

---

6、各行(列)元素和相等的行列式（提取公因式后）【重复】

这类行列式的特征是其所有行(列)对应元素相加后相等

对这类行列式，将其所有行(列)加到第一行(列)或第行(列)，提取公因式后，再把每一行都减去第一行(列)，即可使行列式中出现大量的零元素

---

7、相邻两行(列)对应元素相差K倍型的行列式（逐步作差的方法）

7.1 这类行列式的特征是大部分以数字为元素且相邻两行(列)元素相差1的行列式，采用逐步作差的方法，即可出现大量 +1-1元素，进而出现大量0元素

对这类行列式
    自第一行(列)开始，前行(列)减去后行(列)，或自第n行(列)开始，后行(列)减去前行(列)
    即可出现大量元素为1或-1的行列式再进一步化简即出现大量的零元素

7.2 若相邻两行(列)元素相差倍数k，则前(后)行(列)减去后(前)行(列)的-k倍，，采用逐步作k倍差得方法，可使行列式出现大量的零元素

---

8、范德蒙德型行列式（范德蒙德行列式）【重复】

这类行列式的特征是有逐行(列)元素按方幂递增或递减，对这类行列式可以转化为范德蒙德行列式来计算