LLM底层架构---手撕flashattention1

LLM底层架构---手撕flashattention1

作者：@同济大学 刘越

Github ID：@miracle-techlink

联系邮箱：miracle.techlink@gmail.com

校内邮箱: 2254018@tongji.edu.cn

---

引言

FlashAttention是近年来为优化自注意力机制（Self-Attention）而提出的一种高效算法，旨在解决传统注意力机制在大规模模型训练中的内存和计算瓶颈问题。其通过在硬件层面优化内存访问和计算策略，实现了显著的加速效果，尤其适用于大规模模型的训练。在其原始论文中（FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Aware Computation），作者提出了一种基于硬件友好的设计，使得计算过程中内存使用更加高效，从而加速了训练过程。FlashAttention 在保持精度的同时，显著降低了对 GPU 显存的需求和内存带宽的消耗。本文章参考了李理的博客（FlashAttention: 高效注意力机制的实现与优化），结合自己的理解，对 FlashAttention 的原理进行了详细解读。感谢原作者对其原理深入的解读和推导。

FlashAttention 的优势主要体现在以下几个方面：

1. 显著提升训练速度：通过减少内存访问和计算冗余，FlashAttention 在多个任务上展示了比传统方法更快的训练速度。
2. 内存效率：在不牺牲性能的情况下，显著降低了显存的占用，使得训练更长序列成为可能。
3. 硬件友好性：充分利用 GPU 的内存层次结构，减少了对慢速内存的依赖，从而提高了硬件利用率。

这些特性使得 FlashAttention 成为当前深度学习模型，尤其是自然语言处理和计算机视觉领域中大规模训练的理想选择。

---

FlashAttention 概述

传统的自注意力机制在长序列上具有二次时间复杂度和内存需求，导致计算效率低下。FlashAttention通过使用GPU内存层次结构中的读写操作优化算法，并利用块稀疏性进一步提高性能。实验结果表明，FlashAttention比现有基准线快了15％，并且能够处理更长的上下文长度，从而提高了模型的质量并实现了新的能力。例如，在Path-X挑战赛中，FlashAttention使得模型在序列长度为16K时获得了超过61.4％的准确率。

性能评估

1. BERT 模型训练速度
FlashAttention 在训练 BERT-large 模型时，比传统实现（例如 Nvidia MLPerf 1.1）快 15%。在同样的训练初始化和数据集（Wikipedia）下，FlashAttention 在 8 张 A100 GPU 上的训练时间为 17.4 分钟，相比之下，传统实现的训练时间为 20.0 分钟（见表 1）。这表明 FlashAttention 显著提高了 BERT 的训练速度。

2. GPT-2 模型性能
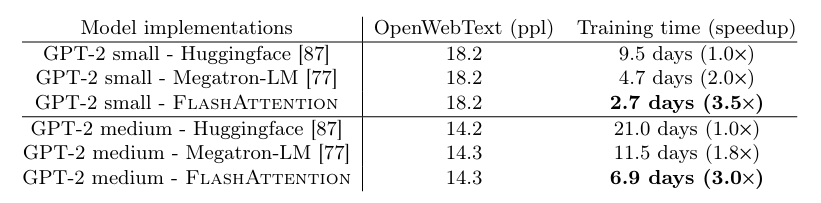
在 GPT-2 上，FlashAttention 同样表现出色。在大规模的 OpenWebText 数据集上，FlashAttention 提供了比 HuggingFace 和 Megatron-LM 实现更快的训练速度。具体而言，GPT-2 small 和 medium 模型使用 FlashAttention 时，比 HuggingFace 实现快 3 倍，比 Megatron-LM 实现快 1.7 倍（见表 2）。FlashAttention 在不改变模型定义的情况下，达到了相同的训练/验证曲线，从而确保了其计算效率。

3. Long-range Arena 基准测试
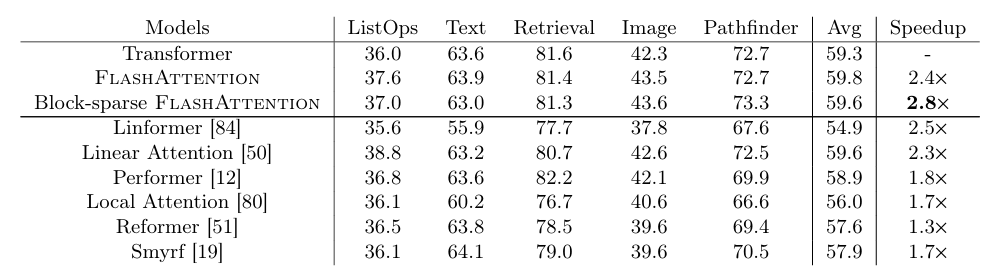
FlashAttention 在 Long-range Arena（LRA）基准测试中表现出色，尤其是在较长序列的处理上。与传统注意力机制相比，FlashAttention 实现了高达 2.4 倍的加速，比所有其他近似方法都要快。特别是，块稀疏 FlashAttention 在处理长序列时展现了更优的速度和效率（见表 3）。

其他优势性能

-训练吞吐量: 衡量模型训练效率的关键指标，通常以每秒处理的 token 数或样本数来表示。FlashAttention 能显著提升吞吐量，实际测试中可达到 2–3 倍的加速效果。这意味着在相同硬件条件下，训练所需时间大幅缩短，实验和调参的反馈周期也随之加快，极大提升了开发效率。

-内存效率: 则体现在显存占用和可支持的最大序列长度上。传统注意力机制的显存复杂度为 O(N²)，而 FlashAttention 通过优化，将其降至 O(N)。这使得在有限的显存资源下，可以处理更长的输入序列和更大的 batch size，进一步提升了模型的表达能力，并减少了对梯度累积等技巧的依赖。

-精度: FlashAttention 不采用任何近似方法，能够保证与标准 Attention 几乎一致的输出结果。无论是从数值误差还是下游任务的性能表现来看，FlashAttention 都能做到训练质量无损，确保模型效果和实验的可复现性。

-硬件友好性: FlashAttention 充分考虑了硬件的内存层次结构，通过优化内存访问模式，减少对慢速内存的依赖，提升了内存带宽利用率和计算单元（如 GPU SM）的占用率。这不仅缓解了显存带宽的瓶颈，还能更好地发挥硬件的并行计算能力，从而提升整体训练效率。

---

内存优化简述

在大规模模型训练中，内存优化是突破性能瓶颈、扩展模型能力的关键。传统自注意力机制在处理长序列时，面临 O(N²) 的显存和计算复杂度，极大限制了可处理的序列长度和 batch size，导致硬件资源难以被充分利用。

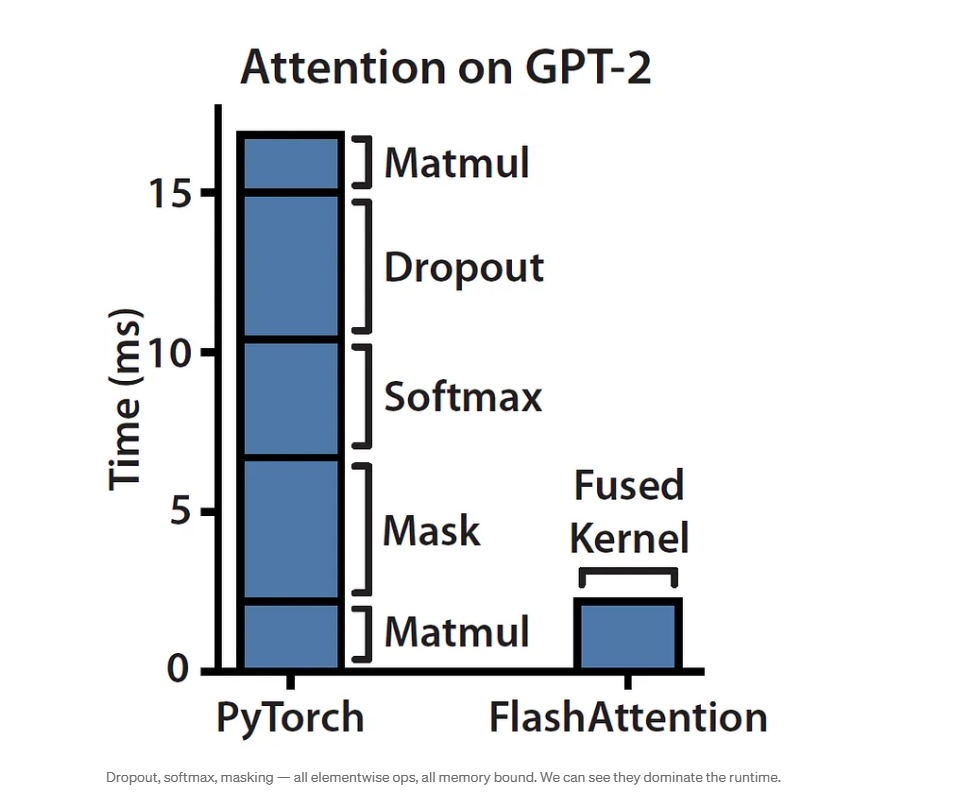
在图中，PyTorch 的处理时间较长，特别是在处理 softmax、dropout、mask 等操作时，这些操作虽然占用了大量的计算 FLOPS，但同时也伴随着内存读写的高开销*。而 FlashAttention 通过内核融合，将这些步骤结合成一个高效的单一操作，减少了中间数据的存储和搬运，从而显著降低了每个步骤的处理时间，尤其是在矩阵乘法（Matmul）和 softmax 操作中，FlashAttention 的优势尤其明显。

FlashAttention 针对这一核心问题，深度结合了现代 GPU 的内存层次结构和高性能计算技术栈，主要包括 CUDA 编程、内核融合（Kernel Fusion）、切块（Tiling）、以及高效的内存调度策略。

---

为什么内存优化比单纯提升 FLOPS 更重要？

在深度学习和大规模模型训练中，很多人习惯用 FLOPS（每秒浮点运算次数）来衡量硬件和算法的性能，认为只要计算能力足够强，训练速度就能大幅提升。然而，实际情况远比这复杂。

• 忽视内存瓶颈：FLOPS 只反映了计算单元的理论算力，却没有考虑数据从内存传输到计算单元的速度。在现代 GPU/CPU 架构下，内存带宽和访问延迟往往成为性能的真正瓶颈。即使计算单元很强大，如果数据无法及时送达，硬件也只能“干等”，无法发挥全部性能。
• 计算停滞现象：当内存访问速度跟不上计算速度时，处理器会频繁陷入等待状态（compute stalls），导致实际利用率远低于理论峰值。此时，单纯提升 FLOPS 并不能带来等比例的性能提升。
• IO 和带宽限制：大模型训练涉及大量数据读写，显存/内存带宽有限，频繁的数据交换会极大拖慢整体速度。FLOPS 的提升无法解决 IO 瓶颈，反而可能让计算资源“吃不饱”。

这里李理以及原作者的博客中有一个很有意思的比喻。

想象一下，计算工厂就像是一个超高效的流水线工人，它能处理大量的任务，一秒钟就能做成很多事（就像是 FLOPS 浮点运算）。但即使它再强大，如果没有足够的原材料（数据）传送给它，它也无法发挥最大效力。这里的“原材料”就是内存——所有的数据都必须从内存中提取出来，才能供给工厂的流水线进行计算。

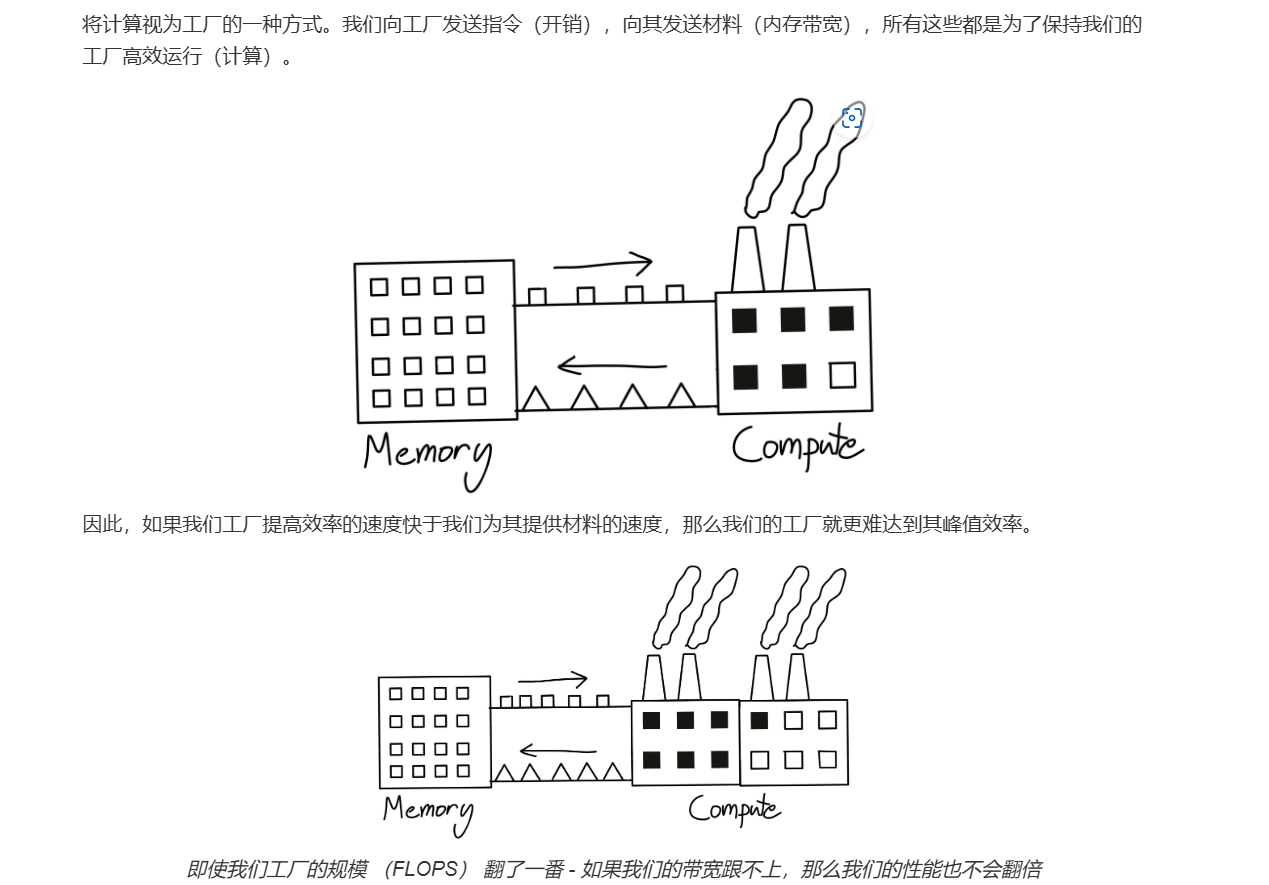
图的上半部分展示了这个生产线的瓶颈——内存和计算之间的平衡。如果内存提供数据的速度跟不上计算的需求，即使你的计算能力再强，也会变得无用。想象一下，这就像工厂的生产线工人再怎么努力工作，却发现没有足够的零件来装配产品。最后，工厂的速度就受限了。

那么，FlashAttention 做了什么呢？它就像是为工厂安装了一条更快速的传送带，使得原材料（数据）能更高效地送到计算工厂。通过减少内存频繁的读写，它优化了数据传输路径，让计算工厂（FLOPS）不再被“原材料短缺”困扰。换句话说，它让内存和计算这两者的合作更加紧密，使得整个生产线（即训练过程）更加高效。

内存带宽的提升就像是加快了数据的输送速度，确保了工厂（计算能力）不至于闲着。而仅仅提升FLOPS，如果没有同步提升内存带宽，那么计算工厂再强大也只是“纸上谈兵”。FlashAttention 精妙的设计让内存和计算两者的配合更加默契，避免了内存和计算的“脱节”，让整个训练过程飞速进行。

---

内存优化策略

在传统的计算中，模型训练可能会受到内存带宽的限制，因为频繁的数据读取和写入会导致计算过程变慢。而 FlashAttention 的优化策略就是通过合理地分配和管理内存，使得最常用的数据（比如在自注意力计算中的矩阵和激活数据）保存在 **GPU 内部的高带宽内存（如 SRAM 和 HBM）**中，这样可以大幅提升数据访问速度。

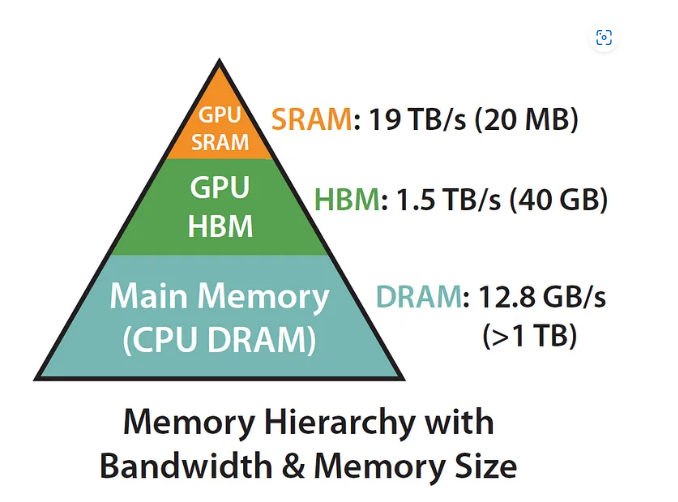
• GPU SRAM： 位于内存层次结构的最上层，具有 最高的带宽（19 TB/s），但容量非常小（仅 20 MB）。这是最快的内存，但因为容量有限，通常仅用于存储频繁访问的小数据。
• GPU HBM： 下一层是 GPU HBM（高带宽内存），带宽为 1.5 TB/s，容量为 40 GB。虽然它的带宽不如 GPU SRAM 快，但比大多数其他内存类型的带宽要高，容量也相对较大。通常用于存储模型数据和高频访问的数据。
• Main Memory (CPU DRAM)：位于最底层的是主内存（CPU DRAM），带宽为 12.8 GB/s，容量大于 1 TB。这部分内存的带宽较低，但其容量是最大的，可以用于存储大量数据。

传统的自注意力计算通常会把大量的数据存储在主内存中，由于主内存的带宽较慢，这会造成计算过程的延迟。而 FlashAttention 通过将数据存储在更接近计算核心的内存中，减少了内存访问的延迟，从而避免了因为带宽限制而导致的性能瓶颈。SRAM 和 HBM这些内存层级提供了极高的带宽和相对较大的容量。FlashAttention 利用这些内存层次的优势，优化了内存访问路径，减少了 GPU 和主内存（CPU DRAM）之间的数据传输，从而加快了计算速度。

---

FlashAttention 能够实现高效的内存优化，核心在于以下三项策略的深度结合与细致实现，可以概括为论文中的这张图片，后面会纤详细的进行解读。

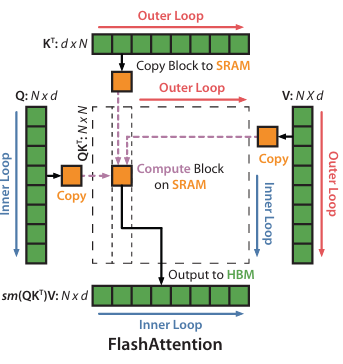
• 切块技术（Tiling）：将大规模矩阵分解为适合 GPU 本地缓存（如 SRAM）的子块，分批次进行计算。这样可以最大化利用高带宽、低延迟的本地存储，减少对慢速 HBM 的访问，提升整体内存带宽利用率。
• 重计算策略(recomputation)：通过重新计算部分中间结果，减少对显存的需求，从而避免显存溢出。同时，通过优化内存访问模式，降低内存带宽的瓶颈，提高计算效率。
• CUDA 优化与内核融合：FlashAttention 通过自定义 CUDA kernel，将多个计算步骤（如 softmax、分数计算等）融合为单一内核，极大减少了内存读写次数，降低了数据在不同操作间的搬运开销。
• 块稀疏性（Block Sparsity）：通过稀疏化注意力矩阵，进一步减少无效计算和冗余内存访问，使得显存资源能够集中用于有效信息的处理。
• 高效内存调度：合理安排数据在 GPU 各级内存（SRAM、HBM）之间的流动，优先利用带宽更高的本地缓存，降低主存访问延迟，避免内存溢出。

后文会详细介绍这几项策略的底层原理，以及如何实现这些策略，相信你读完就会理解这张图的核心思想。

---

Attention计算流程与内存占用分析

在阐述flashattention的优化策略之前，我们先回顾一下attention的计算流程，以及其内存占用情况。

HBM 内存占用分析与优化

我们先来看一下，在原始的attention计算流程中，HBM内存的占用情况。

• 步骤 1：从 HBM 读取 $Q,K$，计算出打分矩阵 $S$ 后，再将 $S$ 全量写入 HBM。
• 步骤 2：再次从 HBM 读取 $S$，做 Softmax 归一化后将概率矩阵 $P$ 全量写回。
• 步骤 3：还要把 $P,V$ 全量计算写回，计算 $O$ 后再全量回写。

每一步都需要大规模地在 HBM 和计算单元之间搬运数据，导致 GPU 计算时常常出现瓶颈，无法充分发挥 FLOP 性能。现代 GPU 在 HBM 与计算核之间存在较快（但小容量的）SRAM（或片上缓存），理想的做法是“分块”把 Q, K, S, P 存在 SRAM，尽量在每次运算时避免访问 HBM。标准实现仍然需要每次读写大部分 HBM，下一步还是需要将全部数据加载到 HBM 中，完全没有利用“缓存亲和性”，浪费了 HBM 与 SRAM 之间的层次优化。

对于长度 $L$ 的序列，$Q$、$K$、$V$ 三个矩阵各占用 $L\times d_k$ 大小的 HBM 容量。打分矩阵 $S=Q{K}^{\top }$ 占用 $L\times L$，概率矩阵 $P=\mathrm{Softmax}(S/\sqrt{d_k})$ 也需要保存同样尺寸。最终输出矩阵 $O=PV$ 则再次占用 $L\times d_k$。

• 总内存峰值：

  $$3L{d}_k+L^2+L^2+L{d}_k=4L{d}_k+2L^2$$

具体来说可以用一下两个指标来衡量计算性能：

• Attention 总 FLOPs：$O(L^2\cdot d_k)$（短矩阵乘法）+ $O(L^2)$（Softmax 缩放）+ $O(L^2\cdot d_k)$，与之对应的内存访问量：读取 Q, K, S, P（每次约 $L^2$），写回 O（每次约 $L\cdot d_k$）。
• Memory-bound：计算大部分都与内存访问密切相关，GPU 核心大部分时间在等待数据，FLOP 数量远大于数据传输能力。

---

从embedding到QKV

Query (Q), Key (K), Value (V) 向量并不是从原始词向量中直接提取的，而是通过对词向量（Embedding）进行线性变换得到的。每个词的 Embedding 向量（例如 $X_1$ 和 $X_2$）都会分别与三个不同的权重矩阵 $W_{\phi }$（分别对应 Q, K, V）进行矩阵乘法，产生 Q, K, V 向量。这三个向量分别代表查询、键和值，最初思想来源于信息检索领域，用于计算查询和文档之间的相关性。

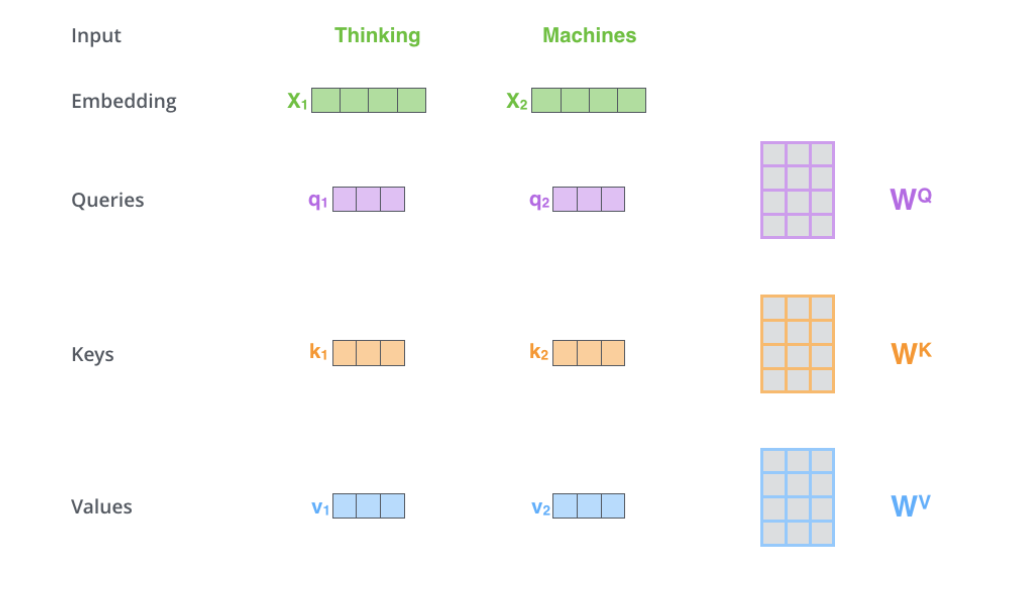
• Q 向量：代表Query,就像你的检索请求：“我想要哪些相关的文档？”。通过乘以权重矩阵 $W_{\phi p}$ 得到 $Q_1$ 和 $Q_2$。这些向量是用来进行查询的。
• K 向量：代表Key，相当于文档的索引或标签：给每个候选文档打上若干关键词。通过乘以权重矩阵 $W_k$ 得到 $K_1$ 和 $K_2$。用于与查询向量进行匹配。
• V 向量：代表value,是存放的实际内容：文档的正文或摘要。通过乘以权重矩阵 $W_v$ 得到 $V_1$ 和 $V_2$。这些向量最终被加权求权，用来计算最终的输出。

---

Scaled Softmax 的作用

Softmax 定义：
$$P_{i,j}=\frac{\exp (S_{i,j})}{{\sum }_{j=1}^L\exp (S_{i,j})}$$

• 归一化：确保每个查询位置 $i$，所有键位置的权重和为 1：${\sum }_j{P}_{i,j}=1$。
• 放大差异：相比线性归一化，更能“放大”相似度较高的项，使注意力更集中。
• 注意力权重：得到的 $P_{i,j}$ 就是注意力分布或“注意力权重”，它告诉模型：在位置 $i$ 生成输出时，应该“关注”输入序列中各个位置 $j$ 的程度。

Scaled Score 和 Softmax 为什么重要？
Scaled Score 通过在计算分数时除以 $\sqrt{d_k}$ 缩放了打分矩阵的数值，避免了当向量维度 $d_k$ 很大时，点积的结果过大，从而导致 Softmax 函数输出极端值的问题。Softmax 使得注意力分布的权重值在合适的范围内，避免了数值不稳定的情况。通过缩放，训练过程的梯度也能保持稳定，避免梯度消失或爆炸的现象。

---

加权输出原理与全局依赖捕捉

加权求和：
$$O=P\cdot V,O_i=\sum _{j=1}^L{P}_{i,j}{V}_j$$

对于输出位置 $i$，每个输入位置 $j$ 的值 $V_j$ 都按注意力权重 $P_{i,j}$ 加权。这样就提升了以下两点能力：
全局依赖：由于每个 $P_{i,j}$ 都考虑了整个序列的打分，输出 $O_i$ 能综合序列中所有位置的信息，突破了 RNN 局限的局部依赖性。多头机制进一步让不同子空间的注意力关注不同范围，提高了捕捉长程依赖的多样性。
增强表示：将上下文中最相关的信息动态集成，使得模型能灵活地聚焦于语义上重要的部分，获得更富表达力的特征表示。

这样，我们就可以去理解attention的核心代码了。

class ScaledDotProductAttention(torch.nn.Module):
    def __init__(self, dropout=0.1):
        super(ScaledDotProductAttention, self).__init__()
        self.dropout = torch.nn.Dropout(dropout)

    def forward(self, Q, K, V, mask=None):
        # Q, K, V: (batch_size, num_heads, seq_len, d_k)
        # mask: (batch_size, 1, seq_len, seq_len)

        d_k = Q.size(-1)  # 键的维度

        # 计算缩放点积注意力
        scores = torch.matmul(Q, K.transpose(-2, -1)) / torch.sqrt(torch.tensor(d_k, dtype=torch.float32))

        # 如果提供了mask，应用mask
        if mask is not None:
            scores = scores.masked_fill(mask == 0, float('-inf'))

        # 使用softmax计算注意力权重
        attention_weights = F.softmax(scores, dim=-1)

        # 为了正则化，应用dropout
        attention_weights = self.dropout(attention_weights)

        # 计算最终的注意力输出
        output = torch.matmul(attention_weights, V)

        return output, attention_weights

---

softmax 切块计算（tiling 技术）

为什么需要 Tiling（切块）？

在自注意力计算中，Softmax 的归一化操作具有“非局部”特性：

$$\sigma (z)i=\frac{\exp (zi)}{\sum {j=1}^K\exp (z_j)}.$$

这里，分母 ${\sum }_{j=1}^K\exp (z_j)$ 要把整行（长度 $N$ ）的所有分数都“读进来”才能计算。这意味着，为了算第 $i$ 个 token 对所有其他 token 的注意力权重，你得先把这一整行的 $score$ 都加载、累加，再做 $Softmax$。

但是SRAM（寄存器 / 片上缓存）非常有限。序列长度 $N\times N$ 在实际应用里常常以几千（$4k$、$8k$）计，有的架构希望跑到( $64k$、$128k$ )。而硬件上能立刻“塞”多少数据到寄存器 / 片上缓存里是受严格限制的，远远装不下整个长度为 $N$ 的行。因此直接算 $N\times N$ 会因为内存或缓存不足而崩溃。

计算 $Attentionscore$ 需要先做

$$Q\cdot K^{\top }$$

得到一个 $N\times N$ 的矩阵，然后对每行做 $Softmax$ ，再乘回去加权

$$O=P\cdot V$$

整个流程如果不分块，当 $N\times N$ 很大时就会因为 SRAM 无法同时容纳整行分数而崩溃。

切块（Tiling）具体方案

• 1.分块 :把大矩阵拆成若干个小块（block），每个小块的行 / 列长度都控制在寄存器能承受的范围内。

• 2.局部计算 :对每个 block 局部做 $Q_{\text{block}}{K}_{\text{block}}^{\top }$ 并累加该 block 内部的 $Softmax$ 计算。

• 3.拼接结果 :将每个 block 的计算结果拼接起来，就能得到完整的注意力矩阵。这样既能保证每次进入 SRAM 的数据量受控，又能拼出完整的注意力矩阵，实现对长序列的高效自注意力计算。

其具体计算过程如下：

给定一个向量 $x=[x_1,\dots ,x_B]$，softmax(x)

计算向量 $x$ 中的最大值，通过减去最大值来避免数值溢出，从而提高计算的稳定性：
$$m(x)=\underset{i}{\max }(x_i)$$

然后，对于每个元素 $x_i$，计算它与最大值 $m(x)$ 之间的差值的指数函数, 这一步将输入的原始数值转化为更容易处理的数值范围，同时保持元素间的相对差异不变：
$$f(x)=[e^{x_1-m(x)},e^{x_2-m(x)},\dots ,e^{x_B-m(x)}]$$

接着，对每个元素的指数值进行累加，得到一个总和，这个步骤是计算 Softmax 输出概率分布的基础：
$$l(x)=\sum _{i}f(x{)}_i$$

最终将每个指数值除以总和，得到 Softmax 归一化的概率分布：
$$\text{softmax}(x)=\frac{f(x)}{l(x)}$$

Softmax计算中，减去最大值 $max(x)$ 的目的是避免数值溢出并确保计算的稳定性。具体原因如下：
$$\begin{array}{rl}& \text{softmax}(1,2,300)=\left[\frac{e^1}{e^1+e^2+e^{300}},\frac{e^1}{e^1+e^2+e^{300}},\frac{e^1}{e^1+e^2+e^{300}}\right]\end{array}$$

$$\begin{array}{rl}& \text{softmax}(1-300,2-300,300-300)=\left[\frac{e^{1-300}}{e^{1-300}+e^{2-300}+e^{300-300}},\frac{e^{2-300}}{e^{1-300}+e^{2-300}+e^{300-300}},\frac{e^{300-300}}{e^{1-300}+e^{2-300}+e^{300-300}}\right]\end{array}$$

我们很容易验证上面两个式子是相等的（只需要把第二个式子的分子分母同时乘以 $e^{300}$）。但是第一种方法是不稳定的，因为 $e^{300}$ 非常大，这就导致上溢。而第二种方法减去最大的数，这就保证最大的是 $e^0=1$，而那些小的数都接近于零。我们知道在 0 到 1 之间，浮点数的精度是最大的。

现在问题来了：我们的 $x\in {\mathbb{R}}^{2B}$ 被切分成两块（后面我们看到多块也是类似的，每次都是合并两块），变成 $x^{(1)}\in {\mathbb{R}}^B$ 和 $x^{(2)}\in {\mathbb{R}}^B$，假设我们可以分别用上面的四个式子计算它们各自的 $m(x^{(1)}/x^{(2)}),f,l,softmax$ 呢？如果可以的话，我们就可以把一个复杂的问题分解成很多简单的小问题，然后逐渐合并小问题的解得到大问题的解。答案当然是可以的，这就是下面的计算公式：

$$\begin{array}{rl}m(x)& =m([x^{(1)},x^{(2)}])=\max (m(x^{(1)}),m(x^{(2)}))\end{array}$$

$$\begin{array}{rl}f(x)& =\left[e^{m(x^{(1)})-m(x)}f(x^{(1)}),e^{m(x^{(2)})-m(x)}f(x^{(2)})\right]\end{array}$$

$$\begin{array}{rl}l(x)& =l([x^{(1)},x^{(2)}])=e^{m(x^{(1)})-m(x)}l(x^{(1)})+e^{m(x^{(2)})-m(x)}l(x^{(2)})\end{array}$$

$$\begin{array}{rl}\text{softmax}(x)& =\frac{f(x)}{l(x)}\end{array}$$

一下是tilling后的代码:

import torch
import torch.nn.functional as F

def softmax(x, dim=-1):
    """
    计算 Softmax，减去最大值来避免数值溢出
    """
    m = torch.max(x, dim=dim, keepdim=True)[0]  # 计算最大值
    f = torch.exp(x - m)  # 计算指数部分
    l = torch.sum(f, dim=dim, keepdim=True)  # 计算累加和
    return f / l  # 返回归一化的概率分布

def tiling_attention(Q, K, B):
    """
    计算基于 Tiling 的 Attention，Q 和 K 是查询（Query）和键（Key）的矩阵，
    B 是每个块的大小（分块的维度）
    """
    # 获取矩阵的形状
    n, d = Q.shape  # Q 的维度 (n, d)
    
    # 初始化结果
    output = torch.zeros((n, n), device=Q.device)
    
    # 对 Q 和 K 按块进行处理
    for i in range(0, n, B):  # 遍历查询矩阵的行块
        for j in range(0, n, B):  # 遍历键矩阵的行块
            # 取出每个块
            Q_block = Q[i:i+B, :]
            K_block = K[j:j+B, :]
            
            # 计算 Q_block 和 K_block 的点积
            attention_scores = torch.matmul(Q_block, K_block.T)  # 计算注意力得分
            
            # 计算每个块的 Softmax
            attention_probs = softmax(attention_scores, dim=-1)  # 计算该块的 Softmax 值
            
            # 将计算结果拼接起来
            output[i:i+B, j:j+B] = attention_probs
    
    return output

# 示例：假设 Q 和 K 是两个大小为 (6, 4) 的矩阵，B=2 表示每个块大小为 2
Q = torch.tensor([[1.0, 2.0, 3.0, 4.0],
                  [2.0, 3.0, 4.0, 5.0],
                  [3.0, 4.0, 5.0, 6.0],
                  [4.0, 5.0, 6.0, 7.0],
                  [5.0, 6.0, 7.0, 8.0],
                  [6.0, 7.0, 8.0, 9.0]])

K = torch.tensor([[1.0, 2.0, 3.0, 4.0],
                  [2.0, 3.0, 4.0, 5.0],
                  [3.0, 4.0, 5.0, 6.0],
                  [4.0, 5.0, 6.0, 7.0],
                  [5.0, 6.0, 7.0, 8.0],
                  [6.0, 7.0, 8.0, 9.0]])

B = 2  # 每个块的大小

# 计算 Tiling 后的 Attention
attention_output = tiling_attention(Q, K, B)

print("Attention Output:")
print(attention_output)

---

重计算（recomputation）优化

核心思想

重计算的本质是用算力换带宽，也就是在计算完 Q_block 和 K_block 的点积后，不立即计算 Softmax，而是将结果存储起来，等到所有块都计算完毕后重算点积，再进行 Softmax 计算。这样可以减少 Softmax 计算的次数，从而提高计算效率。

前向传播重计算后复杂度

同样计算 $S,P,O$：

$$S_{ij}=\frac{Q_i\cdot K_j}{\sqrt{d}},P_{ij}=\mathrm{softmax}(S_{i:}),O=PV.$$

原来需要储存整个 $P\in {\mathbb{R}}^{N\times N}$ ,现在仅需要保存：
输出 $O\in {\mathbb{R}}^{N\times d}$ 和每行 softmax 的归一化统计量：

$$m_i=\underset{j}{\max }{S}_{ij},{\ell }_i=\sum _{j=1}^N\exp (S_{ij}-m_i)(O(N)\text{ 空间}).$$

总内存峰值：
$$O(Nd)+O(N)=O(Nd+N)\approx O(Nd).$$

前向传播重计算前复杂度

1.计算相关矩阵 S：
$$S_{ij}=\frac{Q_i\cdot K_j}{\sqrt{d}},Q,K\in {\mathbb{R}}^{N\times d}$$

• 运算量：每对 $(i,j)$ 要做一次 d 维点积，消耗 d 次乘加。
  总共有 N × N 对，故 FLOPs 是 $N^2\times d=O(N^{2}d)$。

2. 执行 Softmax → 注意力权重 P

$$P_{ij}=\frac{\exp (S_{ij})}{{\sum }_{k=1}^N\exp (S_{ik})}$$

• 运算量：对每行有 N 个元素做指数和归一化，总共 N 行。复杂度是 $O(N^2)$。

3. 加权求和并输出 O

$$O=P\cdot V,V\in {\mathbb{R}}^{N\times d}$$
运算量：知排列法 P (N × N) 和 V (N × d)，需要 N × N × d 次乘加：$$O(N^{2}d)$$

4.合并步骤：

$$O(N^{2}d)+O(N^2)+O(N^{2}d)=O(N^{2}d)(\text{忽略低阶项}O(N^2))$$

5.中间量存储 (Memory)

为了在反向传播中重复用上述结果，前向需要保留：
· 似度矩阵 $S\in {\mathbb{R}}^{N\times N}$，占用 N² 浮点数。
· 注意力权重矩阵 $P\in {\mathbb{R}}^{N\times N}$，占用 N² 浮点数。
· (输出 O 与 V, Q, K 也会保留，但都会分别是 O(Nd) 或可忽略相比 N² 的量。)

因此，峰值显存 / 内存大致是：$$O(N^2)+O(N^2)+O(Nd)\approx O(N^2)$$

反向传播过程

1.重算 $S$ 和 $P$：
$${\tilde{S}}_{ij}=\frac{Q_i\cdot K_j}{\sqrt{d}}-m_i,P_{ij}=\frac{\exp ({\tilde{S}}_{ij})}{{\ell }_i}.$$

2.计算梯度（与 Baseline 相同，只是用重算得来的 $P$）：

已知O的梯度，计算P和V的梯度：

$$\frac{\partial L}{\partial P}=\frac{\partial L}{\partial O}{V}^{\top },\frac{\partial L}{\partial V}=P^{\top }\frac{\partial L}{\partial O},$$

再求S的梯度，利用softmax的公式：

$$\frac{\partial L}{\partial S}=P\odot \frac{\partial L}{\partial P}-P\odot [(P\odot \frac{\partial L}{\partial P})1],$$

最终求Q,K的梯度：

$$\frac{\partial L}{\partial Q}=\frac{1}{\sqrt{d}}\frac{\partial L}{\partial S}K,\frac{\partial L}{\partial K}=\frac{1}{\sqrt{d}}(\frac{\partial L}{\partial S}{)}^{\top }Q.$$

这里无需存储完整 $S,P$，只需在反向阶段多做一次矩阵乘与 softmax 运算。

核融合（Kernel Fusion）原理

前文我们讲了tilling，它使得我们可以在显存不足的情况下，通过分块计算来避免显存溢出。然而，分块计算会带来额外的计算开销，因为我们需要在多个块之间进行通信。为了解决这个问题，我们可以使用核融合技术。“tiling”（分块）策略把算法放在一个 CUDA 核函数中实现。在这个核函数里，会把输入从 HBM 加载进来，然后依次进行一系列的计算操作，包括矩阵乘法、softmax 操作以及可选择性的 “masking（掩蔽）” 和 “dropout（丢弃）” 操作，最后再将计算得到的结果写回到 HBM 中。这种核融合的方式避免了反复地从 HBM 读取输入数据和向 HBM 写入输出数据，有效降低了数据传输带来的性能损耗，提高了整体的计算效率。

伪代码解读

我们来看这段伪代码：

初始化与分块

这一步就是前文我们提到的tilling，将矩阵Q,K,V分块，并初始化输出矩阵O。

设置块大小：
- 列块大小 $B_c=\lceil \frac{4d}{M}\rceil$
- 行块大小 $B_r=\min (\lceil \frac{4d}{M}\rceil ,d)$

初始化变量：
- 输出矩阵 $O=0\in {\mathbb{R}}^{N\times d}$
- 累积变量 $\ell =0\in {\mathbb{R}}^N$
- $m=-\infty \in {\mathbb{R}}^N$

分块处理矩阵：
- 将 $Q$ 分成 $T_r=\lceil \frac{N}{B_r}\rceil$ 个行块 $Q_1,\dots ,Q_{T_r}$，每个块大小为 $B_r\times d$
- 将 $K$ 和 $V$ 分成 $T_c=\lceil \frac{N}{B_c}\rceil$ 个列块 $K_1,\dots ,K_{T_c}$ 和 $V_1,\dots ,V_{T_c}$，每个块大小为 $B_c\times d$
- 将 $O$ 分成 $T_r$ 个行块 $O_1,\dots ,O_{T_r}$，每个块大小为 $B_r\times d$
- 将 $\ell$ 和 $m$ 分成 $T_r$ 个块 ${\ell }_1,\dots ,{\ell }_{T_r}$ 和 $m_1,\dots ,m_{T_r}$，每个块大小为 $B_r$

然后就是外层循环和内层循环了，这段代码中，外层循环遍历列块 $K_j$ 和 $V_j$，内层循环遍历行块 $Q_i$ 和对应的输出块 $O_i$，以及累积变量 ${\ell }_i$ 和 $m_i$，程序会依次将它们从高速内存（HBM）加载到芯片的内存（SRAM）中进行计算。核心思想是利用矩阵乘法的并行性，将计算任务分配到多个计算单元上，从而提高计算效率。

外层循环（训练步骤）
外层循环是针对每一个时间步骤（或训练轮次）的迭代。它涉及对每一组数据进行处理，从而训练模型的参数。通过不断的迭代，模型逐渐优化其参数，使得预测结果接近真实值。

1. 加载数据：外层循环遍历训练过程中的不同时间步骤 $j$（例如每个批次）。
2. 从存储器加载数据：在每一次外层循环中，系统从高带宽内存（HBM）加载键（K）、值（V）向量。
3. 计算注意力分数：对于每一对查询$Q_i$和键$K_j$，计算得到一个注意力矩阵。
4. 更新值与权重：通过计算注意力矩阵的最大值和归一化处理来更新每个查询的权重值（$m_{new,ij}$ 和 ${\ell }_{new,i}$）。
5. 写回更新结果：将更新后的参数和结果写回内存。

内层循环（迭代训练）
内层循环负责根据数据中的具体元素来进一步优化和计算。对于每一个训练样本的输入，通过计算查询与键之间的关系，更新权重值和模型状态。

具体步骤如下：

1. 计算注意力分数：对于每个数据$i$，基于查询向量$Q_i$和键向量$K_j$的内积计算注意力分数$S_{ij}$。
2. 归一化处理：通过对每一行（每个查询）进行最大化处理，得到标准化后的注意力矩阵。然后对矩阵进行指数化，得到归一化后的概率分布（${\tilde{P}}_{ij}$）。
3. 更新模型状态：根据当前的权重（$m_i$ 和 ${\ell }_i$）与计算得到的${\tilde{P}}_{ij}$更新模型的输出$O_i$。
4. 写回存储器：将每次迭代的结果（新的模型参数和权重）写回内存，以便在下一步训练中使用。

训练循环终止
训练会根据设定的迭代次数或者收敛标准进行终止。外层和内层循环会反复进行，直到达到训练目标。

核心代码

import torch
import torch.nn.functional as F

def flash_attention(Q, K, V, mask=None, dropout_p=0.0, block_size=64):
    """
    模拟 FlashAttention 计算：给定查询（Q）、键（K）、值（V），返回加权的值。
    通过块级并行化来减少内存带宽消耗。

    参数:
    - Q: 查询矩阵，形状 (batch_size, num_heads, seq_len, head_dim)
    - K: 键矩阵，形状 (batch_size, num_heads, seq_len, head_dim)
    - V: 值矩阵，形状 (batch_size, num_heads, seq_len, head_dim)
    - mask: 可选的掩码矩阵，形状 (batch_size, 1, seq_len, seq_len)
    - dropout_p: dropout 概率，默认没有 dropout
    - block_size: 用于块级并行化的块大小

    返回:
    - O: 输出矩阵，形状 (batch_size, num_heads, seq_len, head_dim)
    """

    batch_size, num_heads, seq_len, head_dim = Q.size()

    # 计算 Q 和 K 的点积得到注意力得分 S
    S = torch.matmul(Q, K.transpose(-2, -1))  # (batch_size, num_heads, seq_len, seq_len)

    # 应用掩码（如果有的话）
    if mask is not None:
        S = S.masked_fill(mask == 0, float('-inf'))

    # 对得分进行 softmax，得到注意力分布
    P = F.softmax(S, dim=-1)  # (batch_size, num_heads, seq_len, seq_len)

    # 应用 dropout（如果需要）
    if dropout_p > 0.0:
        P = F.dropout(P, p=dropout_p, training=True)

    # 计算加权和 O = P @ V
    O = torch.matmul(P, V)  # (batch_size, num_heads, seq_len, head_dim)

    # 现在模拟块稀疏计算：我们将整个矩阵分成大小为 block_size 的块进行计算
    O_blocked = torch.zeros_like(O)
    for i in range(0, seq_len, block_size):
        for j in range(0, seq_len, block_size):
            # 为了模拟块计算，我们只计算当前块
            S_block = S[:, :, i:i+block_size, j:j+block_size]
            P_block = P[:, :, i:i+block_size, j:j+block_size]
            V_block = V[:, :, j:j+block_size, :]

            # 计算当前块的加权和
            O_blocked[:, :, i:i+block_size, :] = torch.matmul(P_block, V_block)

    return O_blocked


# 使用示例：

batch_size = 2
num_heads = 4
seq_len = 8
head_dim = 8
block_size = 4  # 使用 4x4 的块

# 随机初始化 Q, K, V
Q = torch.randn(batch_size, num_heads, seq_len, head_dim)
K = torch.randn(batch_size, num_heads, seq_len, head_dim)
V = torch.randn(batch_size, num_heads, seq_len, head_dim)

# 创建掩码矩阵
mask = torch.ones(batch_size, 1, seq_len, seq_len)  # 完全有效的掩码

# 调用 FlashAttention
output = flash_attention(Q, K, V, mask=mask, dropout_p=0.1, block_size=block_size)

# 打印输出形状
print(f"Output shape: {output.shape}")

Block-Sparse FlashAttention

块稀疏注意力（Block-Sparse Attention）：这是一种用于减少计算量和内存消耗的技术，特别是在处理大规模数据时非常有效。通过使用稀疏的注意力矩阵，FlashAttention 可以显著减少无效计算。

在上面的图示中，矩阵的非零区域表示的是某些特定块内的计算是“有效”的，而零区域表示无需计算，即这些部分的注意力权重为零。这意味着，在这些区域内，查询和键之间的注意力关系并不需要进行计算，从而节省了计算资源和内存带宽。

每个块内的 token 可以进行注意力计算，也就是说在每个块内，查询和键之间是全连接的。这种方式可以提高效率，避免在计算时涉及到大量不需要计算的区域。比如，第一行的前两个“1”表示第一个 token 只能与第二个和第三个 token 进行注意力计算，其他的 token 由于被掩盖（值为零）而没有进行计算。通过对这些有效的连接进行加速，计算变得更高效。

总结

FlashAttention作为一种创新的自注意力机制优化算法，通过充分利用GPU的内存层次结构和高效的计算策略，成功地解决了传统自注意力机制在处理长序列时的内存和计算瓶颈问题。它在多个深度学习任务中展现了出色的性能，显著提升了训练速度和内存效率，同时减少了对硬件资源的依赖。通过优化矩阵运算、内存访问和数据传输，FlashAttention为大规模模型的训练提供了一个强大的解决方案。

不仅如此，FlashAttention的内存优化策略（如Tiling、重计算和内核融合）以及块稀疏性等技术，使得它能够在不牺牲模型精度的前提下，大幅度降低内存消耗，提高计算效率，尤其是在需要处理超长序列和复杂任务时，展现了独特的优势。

随着深度学习模型规模的不断增长，FlashAttention为解决大模型训练中的资源瓶颈提供了新的思路和方法，未来有望在更广泛的应用场景中发挥更大的作用。希望本文能帮助你更好地理解FlashAttention的优化原理与实践，也期待它在更多领域中的应用与发展。

参考文献

1.FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Aware Computation，arXiv论文链接
2.FlashAttention: 高效注意力机制的实现与优化，李理博客链接
3.Attention Is All You Need，原始论文链接
4.Megatron-LM: Training Multi-Billion Parameter Language Models Using Model Parallelism，原始论文链接
5.Efficient Attention: Attention with Linear Complexities，论文链接
6.Beyond FlashAttention: Exploring Memory-Efficient Transformer Models，研究解读链接